спектральный метод интерполяции [16, 39].

14.4. спектральный метод интерполяции [16, 39].

При дискретизации данных с равномерным шагом по аргументу наиболее точную интерполяцию финитных сигналов обеспечивает спектральный метод. При условии, естественно, что в спектре сигнала не содержится частотных составляющих, превышающих частоту Найквиста.

Спектр дискретного сигнала. Допустим, что для обработки задается произвольный аналоговый сигнал s(t), имеющий фурье-образ S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шаг Dt = 1/F = q) с математических позиций означает умножение функции s(t) на гребневую (решетчатую) функцию Ш_q(t) = 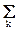d(t-kDt):

s_q(t) = s(t) Ш_q(t) = s(t) 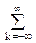d(t-kDt) = 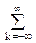s(kDt)d(t-kDt). (14.4.1)

С учетом известного преобразования Фурье гребневой функции Ш_q(t) Û F×Ш_F(f) фурье-образ дискретной функции s_q(t):

S_F(f) = S(f) ③ F×Ш_F(f). (14.4.2)

Ш_F(f) = 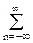d(f-nF). (14.4.3)

Отсюда, для спектра дискретного сигнала имеем:

S_F(f) = F×S(f) ③ 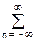d(f-nF) = F 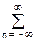S(f-nF). (14.4.4)

Спектр дискретного сигнала представляет собой непрерывную периодическую функцию с периодом F, совпадающую с функцией F×S(f) непрерывного сигнала s(t) в пределах центрального периода от -f_N до f_N, где f_N= 1/2Dt = F/2 - частота Найквиста. Частота дискретизации сигнала должна быть минимум в два раза выше максимальной частотной составляющей в спектре сигнала (F = 1/Dt ³ 2f_max). Умножая функцию (14.4.2) на прямоугольную весовую функцию П_F(f), равную 1 в пределах главного частотного, получаем непрерывный спектр в бесконечных по частоте границах, равный спектру F×S(f) в пределах главного частотного диапазона:

F×S(f) = F×[S(f) ③ Ш_F(f)] П_F(f). (14.4.5)

Обратное преобразование Фурье этого спектра, с учетом коэффициента F, должно восстанавливать непрерывный сигнал, равный исходному аналоговому сигналу s(t).

На рис. 14.4.1 приведен пример интерполяции и экстраполяции равномерных по аргументу дискретных данных в сравнении с сплайн-методом и методом по Лагранжу. Исходная аналоговая кривая дискретизирована корректно (f_max < 1/2Dt) и восстановленная по дискретным данным кривая fS(z) полностью ее повторяет. Близкие результаты к исходному сигналу дает также и сплайн-интерполяция, но доверять сплайн-экстраполяции, особенно по концевой части интервала задания данного сигнала, не приходится. Что касается интерполяции по Лагранжу, то можно видеть существенную погрешность интерполяции на концевых частях интервала сигнала и полную непригодность для задачи экстраполяции.

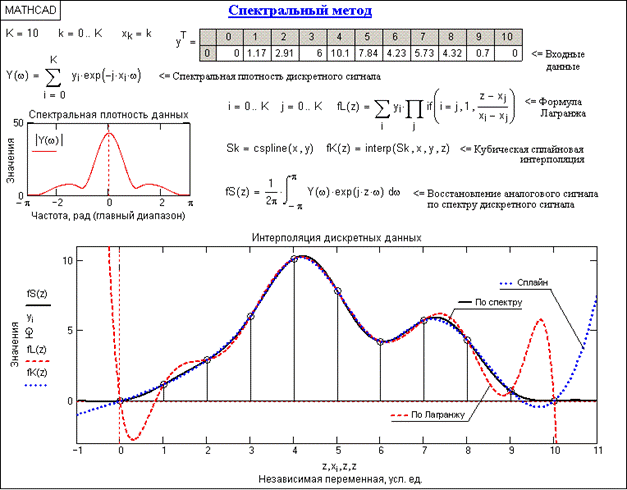
Рис. 14.4.1. Спектральный метод интерполяции и экстраполяции.

Вычисление спектра, учитывая информационную равноценность динамического и спектрального представления сигналов, может производиться в дискретном варианте с использованием быстрого преобразования Фурье.

При нарушении корректности дискретизации данных погрешности интерполяции возрастают практически во всех методах интерполяции. Это можно видеть на рис. 14.4.2, который полностью повторяет рис. 14.4.1 с изменением значения только одного, пятого отсчета (уменьшение с 7.84 до 2), что вызывает подъем высоких частот в спектре данных.

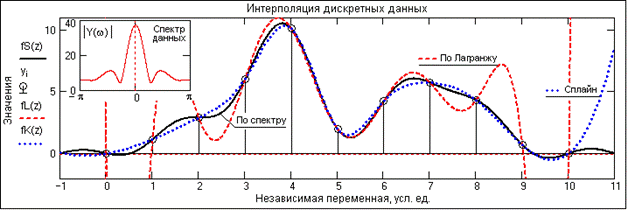
Рис. 14.4.2.

Следует учитывать, что при интерполяции данных, представляющих собой вырезки из сигнальных функций с определенной постоянной составляющей (сигнал не выходит на нулевые значения на концевых участках интервала задания), а равно и любых данных со скачками функций, при спектральном преобразовании на интерполированном сигнале в окрестностях обрезания данных и скачков возникает явление Гиббса. Это можно видеть сравнением рисунков 14.4.1 и 14.4.3. Данные на рис. 14.4.1 в рисунке 14.4.3 подняты на 20 единиц постоянной составляющей.

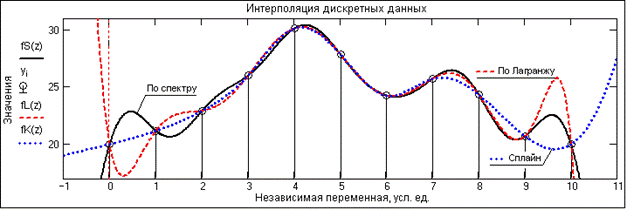
Рис. 14.4.3.

Для исключения этого эффекта можно рекомендовать перед интерполяцией производить определение линейного тренда данных по концевым значениям отсчетов и вычитать его из данных, с последующим восстановлением после интерполяции.

Интерполяционный ряд Котельникова-Шеннона.Произведем обратное преобразование обеих частей равенства (14.4.5). Умножение непрерывного и бесконечного спектра на П-импульс в пределах главного диапазона отобразится в динамической области сверткой двух функций:

F×s(t) = F×s_q(t) ③ sinc(pFt).

s(t) = sinc(pFt) ③ 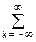s(kDt)d(t-kDt),

Отсюда, с учетом равенства d(t-kDt) ③ sinc(pFt) = sinc[pF(t-kDt)], получаем:

s(t) = 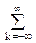s(kDt) sinc[pF(t-kDt)]. (14.4.6)

Эта формула носит название интерполяционного ряда Котельникова-Шеннона и, по существу, является разложением сигнала по системе ортогональных функций sinc(pF(t-kDt)) = sinc(p(t/Dt – k)). С другой стороны, эта формула представляет собой свертку дискретной функции данных s(kDt) с непрерывной функцией интегрального синуса. Для больших массивов дискретных данных точность восстановления сигнала обычно ограничивается интервалом задания функции интегрального синуса, по которому устанавливается интервал суммирования.

Из совокупности приведенных формул следует, что если для частоты дискретизации сигнала справедливо неравенство F ³ 2f_max, где f_max- наибольшая частота в спектре произвольной непрерывной функции s(t), то функция s(t) может представляться в виде числовой последовательности дискретных значений s(kDt), k = 0,1,2,..., и однозначно по этой последовательности восстанавливаться, в пределе - без потери точности. В этом и состоит сущность теоремы отсчетов Котельникова-Шеннона.

На рис. 14.4.4 приведен пример интерполяции входных данных, повторяющих данные рис. 14.4.1. Результаты интерполяции, как и следовало ожидать, абсолютно идентичны. Аналогичным образом влияют на результаты усечение и скачки функций (явление Гиббса).

Рис. 14.4.4. Интерполяция по Котельникову-Шеннону.

14.5. ДЕЦИМАЦИЯ И ИНТЕРПОЛЯЦИЯ ЦИФРОВЫХ СИГНАЛОВ [43]

Применительно к цифровым сигналам децимация – уменьшение частоты дискретизации данных с сохранением в новом сигнале всей полезной информации. Интерполяция обратна децимации – увеличение частоты дискретизации без изменения информации. Цифровая децимация и интерполяция широко используется в современных системах обработки данных для сжатия и восстановления данных, для уменьшения объемов памяти хранения данных, для увеличения скорости передачи данных, и т.п.

Простой, но мало производительный подход – восстановить сигнал в аналоговой форме (ЦАП) и заново оцифровать его (АЦП) с новой частотой дискретизации. Цифровые методы позволяют выполнить эту операцию в более эффективной форме.

Децимация с целым шагом. Кратная компрессия частоты дискретизации снижает частоту дискретизации входного сигнала x(k) с f_d до f_d/M путем отбрасывания М-1 отсчетов в каждой последовательной серии из М-отсчетов, т.е. из М-отсчетов оставляется только 1:

y(m) = 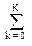x(k) d(k-mM), m = 0, 1, 2, … , K/M. (14.5.1)

Естественно, что частота Найквиста f_N входного сигнала x(k) компрессора для выходного сигнала y(k) также уменьшается в М раз и становится равной f_N' = f_N/M для выходного сигнала. Для полного сохранения после компрессии полезной информации, содержащейся в сигнале x(k), максимальная частота полезной информации во входном сигнале не должна превышать значения f_max £ f_N/2M. В противном случае децимация будет некорректной и в новом главном частотном диапазоне выходного сигнала произойдет искажение спектра полезной информации за счет сложения со спектрами боковых диапазонов. Пример корректной децимации сигнала с М=2 и спектры входного и децимированного сигнала приведены на рис. 14.5.1.

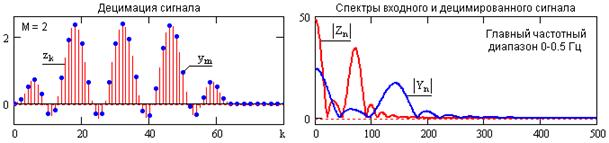
Рис. 14.5.1.

Входные сигналы кроме полезной информации могут содержать статистические шумы и помехи, распределенные по всему частотному диапазону. При децимации шумы и помехи в частотном диапазоне от f_N/M до f_N входного сигнала зеркально отражаются от f_N' нового главного частотного диапазона и их суммирование со спектром нового главного диапазона и полезного сигнала может приводить к увеличению уровня шумов и искажению информации. Для исключения этого эффекта перед конверсией сигнала необходимо выполнять его низкочастотную фильтрацию со срезом на частоте f_N/2M.

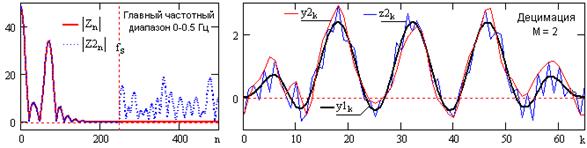
Рис. 14.5.2.

На рис. 14.5.2 приведен спектр Z2_n сигнала z_k с рисунка 14.5.1 (спектр Z_n), в который для наглядности эффекта зеркального отражения условно введен только высокочастотный шум на интервале f_s - f_N, и соответствующий данному спектру сигнал z2_k. При децимации сигнала z2 с М=2 сначала была выполнена его низкочастотная фильтрация с частотой среза f_s, что полностью сняло модельный шум, и при восстановлении сигнала (интерполяции) получен сигнал y1_k, полностью соответствующий сигналу z_k. При выполнении децимации без предварительной фильтрации восстанавливается сигнал y2_k, который по своей форме отличается как от сигнала y1_k = z_k, так и от входного сигнала z2_k.

Интерполяция с целым шагом. Экспандер частоты дискретизации увеличивает частоту дискретизации входного сигнала x_k с f_d до Lf_d путем введения (L-1) нулевых отсчетов после каждого отсчета входного сигнала. При этом форма спектра выходного сигнала y_k остается без изменения, но частотная шкала спектра сжимается в L раз и в границы главного диапазона спектра входного сигнала ±f_N заходят боковые диапазоны спектра выходного сигнала (зеркальные частоты). Это наглядно можно видеть на рис. 14.5.3 сравнением спектров X_n для входного сигнала x_k, и Y_n для экспандированного сигнала x_k с L=2. Следовательно, фактическая частота Найквиста выходного сигнала становится равной f_N/L. Для исключения зеркальных частот и распределения энергии отсчетов x_k по L выходным интервалам экспандированный сигнал пропускается через фильтр нижних частот со срезом на частоте f_N/L и с коэффициентом L для компенсации распределения энергии отсчетов по интервалам L. Результат операции можно видеть на сигнале y_k по сравнению с исходным сигналом z_k (рис. 14.5.1), децимацией которого с М=2 был получен сигнал x_k.

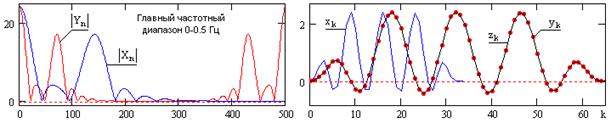
Рис. 14.5.3.

Преобразование частоты дискретизации с нецелым шагом на практике обычно выполняют представлением нецелого множителя максимально близким приближением рациональными числами вида L/M, Это позволяет выполнять преобразование частоты дискретизации последовательными операциями сначала интерполяции с шагом L, сохраняющей все частотные составляющие сигнала, и затем децимации с шагом М, при которой часть высокочастотных составляющих и шумов будет подавлена низкочастотной фильтрацией. Поскольку при этом низкочастотные фильтры экспандирования и децимации следуют друг за другом и работают на одной частоте дискретизации, то вместо двух фильтров можно применять один, имеющий минимальную частоту среза с коэффициентом усиления, равным L.

При программной обработке больших пакетов данных децимация и интерполяция может выполняться в спектральной области с использованием БПФ.

⇐ Предыдущая 1 2 345 Следующая ⇒