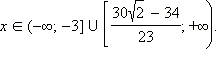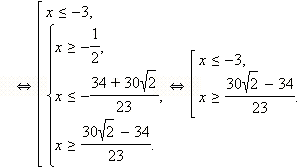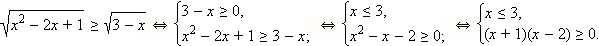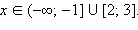- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. Лекция Иррациональные неравенства. Неравенства вида
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Лекция Иррациональные неравенства
Цели урока: повторить основныепонятия, связанные с иррациональными уравнениями, неравенствами ; формирование навыков решения иррациональных уравнений, неравенств
Повторить :
1. Метод интервалов
2. Методы решения иррациональных уравнений
Иррациональным называется неравенство, содержащее переменную под знаком радикала (корня).
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т. д.
Однако при преобразования неравенств, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны.
1. Неравенства вида
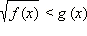
Если x лежит в ОДЗ: f (x) ≥ 0, то левая часть неравенства существует и неотрицательна. Поскольку для всех x, являющихся решением данного неравенства, правая часть больше левой, то g (x) > 0. Следовательно, обе части неравенства неотрицательны (для тех x, которые являются решениями неравенства, другие x нас не интересуют). Значит, возведение в квадрат не нарушает равносильности и можно записать равносильную нашему неравенству систему неравенств:
Метод решения:
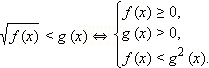
|
Совместно решаем систему неравенств.
Пример 1
 Решение
Решение
Сразу перейдём к равносильной системе:
Ответ. |
Пример 2
Решите неравенство 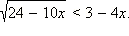
Решение
Перейдём к равносильной системе:
Ответ. |
2. Неравенства вида 
ОДЗ данного неравенства f (x) ≥ 0. Пусть для каких-то x из ОДЗ g (x) < 0. Тогда, очевидно, все эти x − решения, так как при этих x левая часть определена (x 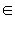 ОДЗ) и неотрицательна, в то время как правая часть g (x) < 0.
ОДЗ) и неотрицательна, в то время как правая часть g (x) < 0.
Для других x из ОДЗ g (x) ≥ 0. Для них обе части неравенства неотрицательны, и его можно возвести в квадрат: 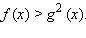 Значит, данное неравенство равносильно совокупности неравенств:
Значит, данное неравенство равносильно совокупности неравенств:
Метод решения:
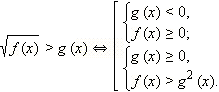
|
Заметим, что в последнюю систему не входит требование f (x) ≥ 0. Оно и не нужно, так как выполняется автоматически 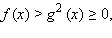 ибо полный квадрат всегда неотрицателен.
ибо полный квадрат всегда неотрицателен.
Пример 3
Решите неравенство 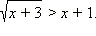
Решение
ОДЗ неравенства: x ≥ –3.
1. Если  то все эти x то все эти x 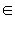 ОДЗ, для которых верно x < –1, − решения. Таким образом, ОДЗ, для которых верно x < –1, − решения. Таким образом, 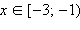 − первая часть ответа.
2. Если − первая часть ответа.
2. Если 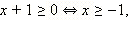 то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем: то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем:
Получаем, что решениями являются все Объединяя результаты пунктов 1 и 2, получаем: Ответ. |
Пример 4
Решите неравенство 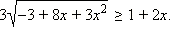
Решение
ОДЗ данного неравенства:  Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.
1. Если Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.
1. Если 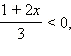 то есть то есть 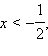 то все такие x из ОДЗ, удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ≤ –3 − решения неравенства.
2. Если то все такие x из ОДЗ, удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ≤ –3 − решения неравенства.
2. Если 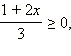 то есть то есть  а с учетом ОДЗ это означает, что а с учетом ОДЗ это означает, что 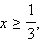 то обе части неравенства неотрицательны. Возведём обе части неравенства в квадрат: то обе части неравенства неотрицательны. Возведём обе части неравенства в квадрат:
Уравнение
Запишем это решение другим способом:
Ответ. |
3. Неравенства вида 
ОДЗ данного неравенства: 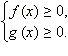 Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему

|
Заметим, что из неравенства 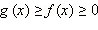 следует, что
следует, что 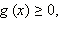 то есть дополнительно это требовать и включать это неравенство в систему не нужно.
то есть дополнительно это требовать и включать это неравенство в систему не нужно.
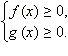
Пример 5
Решите неравенство 
Решение
Перейдём к равносильной системе:
Решая эту систему методом интервалов, сразу получаем: Ответ. |
ВЫВОДЫ:
Алгоритм решения иррациональных неравенств:
1. Уединяем радикал .
2. Находим ОДЗ ( в зависимости от типа неравенства)
3.Возводим обе части неравенства в n-ую степень. Решаем полученное неравенство
( находим корни, определяем интервалы на числовой оси с соответствующими знаками- «-« или « +».)
5. Записываем ответ с учетом ОДЗ.( Т.е. находим совместное решение неравенства с учетом ОДЗ).
Самостоятельно:
Решить примеры:
1. 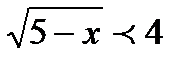
2. 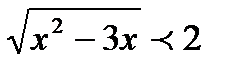
3. 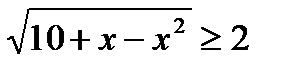
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
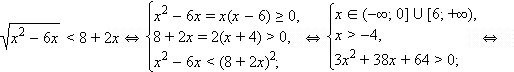
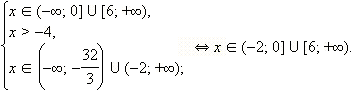
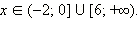
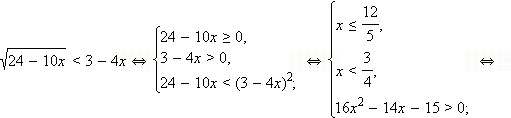

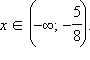
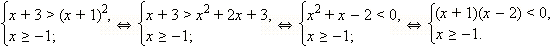
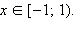
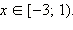
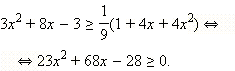
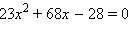 имеет корни
имеет корни  и
и 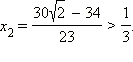 Значит, решением неравенства являются
Значит, решением неравенства являются 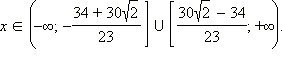 С учётом
С учётом 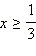 получается, что на данном множестве решениями являются
получается, что на данном множестве решениями являются 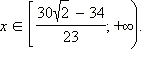 Объединяя результаты пунктов 1 и 2, получаем
Объединяя результаты пунктов 1 и 2, получаем