
Главная
Контакты
Случайная статья
|
Виды призм.
| Класс
|
| | Дата
| 24.02.21 г.
| | Предмет
| математика
| | Тема
| Площадь боковой и полной поверхности призмы
| | Цель
| повторить определение призмы, ее элементов, вывести формулы площади боковой поверхности призмы, продолжить формирование навыков решения задач;
| | Актуализация знаний:
| Определение призмы. Многогранник, составленный из двух равных многоугольников А1 А2…Аn и В1 В2…Вn, расположенных в параллельных плоскостях и n параллелограммов, называется призмой.
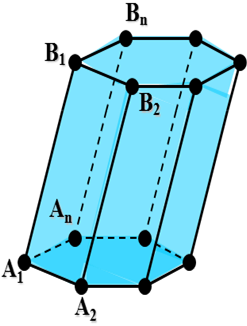
| Элементы призмы.
1. Вершины…
2.Ребра оснований …
3. Боковые ребра …
4.Основания…
5. Боковые грани …
6. Высоты …
7. Диагонали…
8. Диагонали боковых граней…
9. Диагонали оснований…
10. Угол между боковым ребром и основанием….
11. Двугранный угол с ребром А1В1
12. Двугранный угол с ребром А1А2
13. Боковая поверхность призмы.
14. Полная поверхность призмы.
15. Объем призмы.
| Свойства.
2.Противоположные ребра параллельны и равны.
3.Все боковые ребра равны и параллельны.
4.Основания равны и параллельны.
5. Все боковые грани являются параллелограммами. Противоположные боковые грани равны и параллельны.
6. Высота перпендикулярна каждому основанию.
7. Диагонали пересекаются в одной точке и делятся в ней пополам.
11,12. Двугранный угол измеряется линейным углом.
13. Sбок равна сумме площадей боковых граней.
14. Sпол= Sбок+2Sосн
15. V= Sосн∙Н
| |
2.Виды призм.
· а) По виду оснований.
треугольная 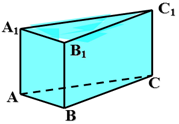
| 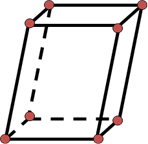 четырехугольная четырехугольная
|  шестиугольная шестиугольная
| · б)По расположению боковых ребер к основанию.
Прямая призма. Прямойназывают такую призму,
боковые ребра которой перпендикулярны к основаниям. 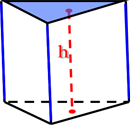
| Наклонная призма
Наклоннойназывают такую призму, боковые ребра
которой не будут перпендикулярны к основаниям. 
| | Свойства.
1. Боковые грани-прямоугольники.
2.Высота равна с боковому ребру.
3. Sбок = Росн∙ Н, Росн- периметр основания призмы, Н- боковое ребро.
4. Sпол= Sбок+2Sосн
5. V= Sосн∙Н
| Свойства.
1. Боковые грани-параллелограммы.
2.Высоты не совпадают с боковыми ребрами.
3. Sбок = Рперпенд. сеч∙ L, Рперпенд. сеч - периметр перпендикулярного сечения призмы, L- боковое ребро.
4. Sпол= Sбок+2Sосн
5. V= Sосн∙Н
| |
| | Изучить п.20-21
Задача №1: сторона основания правильной треугольной призмы равна 6см., а диагональ боковой грани равна 10см. Найти площадь боковой и полной поверхности призмы. (пояснение)
Проверка: Sпов = Sбок+2 Sосн Sбок = Рh Росн.=3·6=18 (см2) Sбок = Рh Sбок=18·8=144(см2) Sосн.= 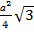 . Sосн=62 . Sосн=62 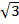 /4=9 /4=9 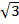 см2 h= см2 h= 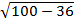 =8(см.) Sпов = Sбок+2 Sосн. Sпов=144+2·9 =8(см.) Sпов = Sбок+2 Sосн. Sпов=144+2·9 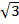 =144+18 =144+18 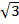 (см2) Ответ: 144+18 (см2) Ответ: 144+18 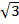 (см2)
Решить №708, 711, 744 (см2)
Решить №708, 711, 744
|
| Практическая часть:
| Тест. 1 вариант.
1). Призма – это выпуклый многогранник, который состоит из:
а) многоугольника и нескольких параллелограммов
б) двух равных многоугольников и нескольких параллелограммов
в) двух равных многоугольников, лежащих в параллельных плоскостях,
и п параллелограммов
2). В основании призмы лежит:
а) любой выпуклый многоугольник
б) только правильный многоугольник
в) любой многоугольник или окружность
3). Призма является прямой, если:
а) боковые ребра перпендикулярны основаниям
б) основания – правильные многоугольники
в) некоторые боковые грани – квадраты
4). Призма является правильной, если:
а) в основании лежит правильный многоугольник
б) боковые грани перпендикулярны основаниям
в) она прямая и в основании лежит правильный многоугольник
5). Высотой прямой призмы можно считать:
а) ребро основания
б) боковое ребро
в) любой отрезок, перпендикулярный основанию
6). Площадь боковой поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей двух оснований
в) сумма площадей всех её граней
7). Площадь полной поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей двух оснований
в) сумма площадей всех её граней
8). Площадь боковой поверхности прямой призмы можно найти по формуле:
а) Sбок=Sосн·h
б) Sбок=а·h, где а – сторона основания
в) Sбок=Росн·h
9). Площадь полной поверхности прямой призмы можно найти по формуле:
а) Sполн=Sосн+ Sбок
б) Sполн=2Sосн+ Sбок
в) Sполн=2Росн+ Sбок
10) Прямоугольный параллелепипед имеет три измерения, равные a=5 см, b=8 см, h =10 см. Площадь его полной поверхности равна.
Тест. 2 вариант.
1). Призма – это выпуклый многогранник, который состоит из:
а) двух равных многоугольников, лежащих в параллельных плоскостях,
и п параллелограммов
б) двух равных многоугольников и нескольких параллелограммов
в) многоугольника и нескольких параллелограммов
2). В основании призмы лежит:
а) только правильный многоугольник
б) любой многоугольник или окружность
в) любой выпуклый многоугольник
3). Призма является прямой, если:
а) некоторые боковые грани – квадраты
б) боковые ребра перпендикулярны основаниям
в) основания – правильные многоугольники
4). Призма является правильной, если:
а) в основании лежит правильный многоугольник
б) она прямая и в основании лежит правильный многоугольник
в) боковые грани перпендикулярны основаниям
5). Высотой прямой призмы можно считать:
а) боковое ребро
б) любой отрезок, перпендикулярный основанию
в) ребро основания
6). Площадь боковой поверхности призмы – это:
а) сумма площадей всех её граней
б) сумма площадей двух оснований
в) сумма площадей всех боковых граней
7). Площадь полной поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей всех её граней
в) сумма площадей двух оснований
8). Площадь боковой поверхности прямой призмы можно найти по формуле:
а) Sбок=Росн·h
б) Sбок=Sосн·h
в) Sбок=а·h, где а – сторона основания
9). Площадь полной поверхности прямой призмы можно найти по формуле:
а) Sполн=Sосн+ Sбок
б) Sполн=2Росн+ Sбок
в) Sполн=2Sосн+ Sбок
10) Прямоугольный параллелепипед имеет три измерения, равные a=4 см, b=5 см, h =11 см. Площадь его полной поверхности равна
|
| Домашнее
задание
| Повторить п.20, 21, решить № 709, 745
|
| Обратная связь
| Сделайте фотографию страниц тетради и классной и домашней работы и в личном сообщении в ВК вышлите.
|
| Сроки выполнения
| 25.02.21 г.
|
| Сроки сдачи
| 25.02.21 г.
|


 четырехугольная
четырехугольная
 шестиугольная
шестиугольная


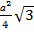 . Sосн=62
. Sосн=62 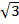 /4=9
/4=9 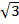 см2 h=
см2 h= 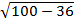 =8(см.) Sпов = Sбок+2 Sосн. Sпов=144+2·9
=8(см.) Sпов = Sбок+2 Sосн. Sпов=144+2·9 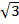 =144+18
=144+18 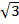 (см2) Ответ: 144+18
(см2) Ответ: 144+18 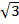 (см2)
Решить №708, 711, 744
(см2)
Решить №708, 711, 744
