Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Тақырып 1. Вакуумдағы манит өрісі

Тақырып 1. Вакуумдағы манит өрісі

Магнит өрісі екі физикалық шамамаен сипатталады: магнит индукциясының векторы [B] = [Тл]         (макро- және микротоқта) және кернеулік векторы 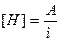(макротоқта)   .

В = mm₀Н

m₀ = 4p×10^-7 Гн/м – магнит тұрақтысы;

m - ортаның магнит өтімділігі

Магнит өрісінің күш сызықтары бұрылғы                ережесімен анықталады

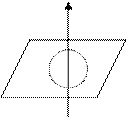   I                             

      A                         

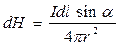 I тоғы бар ұзындығы, dl элемент белгілі А нүктесінде dН кернеулігі Био-Савара-Лаплас заңымен анықталады

Магнит өрісі үшін  суперпозиция принципі анықталады:

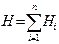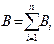1. Шексіз ұзын өткізгіш үшін магнит өрісінің кернеулігі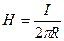            

2. Ұзындығы шектелген өткізгіш үшін магнит өрісінің кернеулігі                 

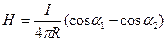
3. Айнымалы тоқтың ортасындағы магнит өрісінің кернеулігі                 

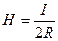
 4. Айнымалы тоқтың осіндегі магнит өрісінің кернеулігі                 

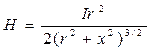х – айнымалы тоқтын осәнде орналасқан кез келген нүктеге дейінгі қашықтық

ТОғы бар өткізгішке магнит өрісі жағынан Ампер күші әсе етеді                           

               F_A = IBl sina    -   Ампер күші

a - өткізгіштің ұзындығы мен магнит индукция векторының арасындағы бұрыш.

Ампер күшінің бағыты сол қол ережесімен анықталады

Екі параллель тоқтар үшін Ампер заңы:

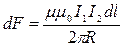 -   Ампер заңы

Қарама қарсы тоқтар тебіледі, бағыттыас тоқтар өзара тартылады

Магнит индукциясының векторының ағыны (магнит ағыны) dS  ауданын сүзіп өтетін өріске перпендикуляр күш сызықтарының санына тең

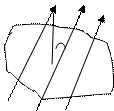
                          B                      Ф = ВScosa - магнитн ағыны

 S                                       

                  S                   

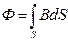
Егер бет тұйықталған болса, онда толық магнит индукциясының векторының ағыны                                                                

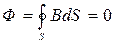                             - магнит өрісі үшін Остроградский-Гаусс теоремасы

Магнит өрісі тек өткізгішке ғана емес, жеке зарядталған бөлшектерге де әсер етеді

υ жылдамдықпен қозғалатын магнит өрісінднгі q зарядқа әсер ететін магнит өрісінің күші Лоренц күші деп аталады.

                        F_л = qυBsina -   Лоренц күші

Ньютонның екінші заңы бойынша бқл күш центрге тартқыш үдеу тудырады

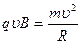
Яғни бөлшек радиусы R болатын шеңбер бойымен қозғалады

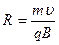
Егер зарядқа электр өрісі әсер етсе, онда толық күш Лоренц формуласымен анықталады

                                   F = qE + qυB –   Лоренц формуласы