
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Двугранный угол. Перпендикулярность плоскостей
Тест № 8
Двугранный угол. Перпендикулярность плоскостей
I вариант
1. Точка А находится на расстоянии 3 см и 5 см от двух перпендикулярных плоскостей. Най-
дите расстояние от точки А до прямой пересечения этих плоскостей.
а) 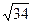 см; б) 4 см; в) 6 см;
см; б) 4 см; в) 6 см;
г) 2 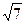 см; д)
см; д) 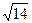 см.
см.
2. Расстояния от точки M до вершин прямо-
угольного треугольника ABC ( 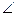 C = 90°) равны. Какое из следующих утверждений верно?
C = 90°) равны. Какое из следующих утверждений верно?
а) Плоскости МАВ и ABC перпендикулярны;
б) плоскости МВС и ABC перпендикулярны;
в) плоскости MAC и ABC перпендикулярны;
г) плоскости MAC и МВС перпендикулярны;
д) условия в пунктах а — г неверны.
3. Плоскости αиβ пересекаются по прямой с.
Плоскость γ перпендикулярна плоскости α, но не
перпендикулярна плоскости β. Выясните взаим-
ное расположение прямой с и плоскости γ.
а) с 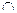 γ; б) c || γ
γ; б) c || γ  ; в) c
; в) c 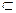 γ ;
γ ;
г) определить нельзя;
д) с уверенностью можно сказать только то, что
прямая с не перпендикулярна плоскости γ.
4. При пересечении двух плоскостей образова-
лись двугранные углы, один из которых в два раза
больше другого. Найдите градусную меру угла меж-
ду этими плоскостями.
а) 30°; б)60°; в) 90°; г) 120°; д) 150°.
5. Равнобедренные треугольники ABC и BDC,
каждый из которых имеет основание ВС, не лежат
в одной плоскости. Их высоты, проведенные к ос-
нованию, равны 5 см, и расстояние между точка-
ми А и D также равно 5 см. Найдите градусную
меру двугранного угла ABCD.
а) 60°; 6)120°; в) 30°; г) 45°; д) 90°.
6. Отрезок AM является перпендикуляром к пло-
скости прямоугольника ABCD. Угол между прямой
MС и этой плоскостью равен 30°. AD = 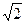 ,CD = 2. Найдите величину двугранного угла MCDA.
,CD = 2. Найдите величину двугранного угла MCDA.
а) определить нельзя; б) 45°;
в) 30°; г) 60°; д) 90°.
7. Какое из следующих утверждений верно?
а) Двугранным углом называется фигура, обра-
зованная прямой а и двумя полуплоскостями с
общей границей a;
б) двугранный угол имеет бесконечное множест-
во различных линейных углов;
в) градусной мерой двугранного угла называется
градусная мера его линейного угла;
г) угол между пересекающимися плоскостями
может быть тупым;
д) если одна из двух плоскостей проходит через
прямую, пересекающую другую плоскость, то та-
кие плоскости перпендикулярны.
8. Гипотенуза прямоугольного равнобедренного
треугольника лежит в плоскости α, а катет накло-
нен к этой плоскости под углом 30°. Найдите угол
между плоскостью α и плоскостью треугольника, а) 90°; б) 60°; в) 45°; г) 30°;
д) определить нельзя.
9. Найдите двугранный угол ABCD тетраэдра
ABCD, если углы DAB, DAC и АСВ прямые,
АС= ВС= 5, AD = 5 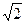 .
.
a) arccos5 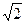 ; б) arcsin5
; б) arcsin5 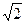 ;
;
в) arcctg 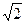 ; г)arctg
; г)arctg 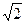 ;
;
д) определить нельзя.
10. В равнобедренном треугольнике ABC AC =
= ВС = 2, 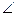 BAC = 30°. Отрезок СМ - перпенди
BAC = 30°. Отрезок СМ - перпенди
куляр к плоскости ABC, CM = 2 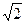 . Найдите ве-
. Найдите ве-
личину двугранного угла МАВС.
a) arctg2; б) arctg2 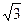 ; в) определить нельзя;
; в) определить нельзя;
г) arctg4; д) arctg 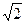 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|