Перпендикуляр и наклонные. Угол между прямой и плоскостью

Тест № 7

Перпендикуляр и наклонные. Угол между прямой и плоскостью

I вариант

1. Из точки М к плоскости α проведены две

наклонные, длины которых 18 см и 2 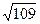см. Их проекции на эту плоскость относятся как 3 : 4. Найдите расстояние от точки М до плоскости α. a)6 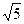cm; б) 30 см; в) 6 см;

г) 3 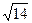cm; д) 2 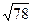см.

2. Какое из следующих утверждений неверно?

а) Перпендикуляр и наклонная, выходящие из
одной точки, имеют разную длину;

б) расстоянием от точки до плоскости называет-
ся длина перпендикуляра, проведенного из данной
точки к данной плоскости;

в) равные наклонные, проведенные к плоскости
из одной точки, имеют разные проекции;

г) проекцией точки на плоскость является точка;

д) углом между прямой и плоскостью, пересека-
ющей эту прямую и неперпендикулярной к ней,
называется угол между прямой и ее проекцией на
эту плоскость.

3. Расстояние от точки M до каждой из вершин
правильного треугольника ABC равно 4 см.. Най-
дите расстояние от точки М до плоскости ABC,
если АВ = 6 см.

а) 4 см; б) 16-2 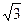см; в) 8 см; г) 6 см; д) 2 см.

4. Через точку А, удаленную от плоскости α на
4 см, проходит прямая, пересекающая плоскость
α в точке В. Найдите угол между прямой АВ и
плоскостью α, если длина отрезка АВ равна 6 см.

a) arccos 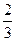; б) arcsin 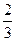; в) arcsin ;

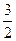г) arctg 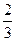; д) arcctg .

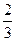5. Из точки к плоскости проведены две равные
наклонные. Величина угла между этими наклонны-
ми равна 60°. Величина угла между их проекция
ми равна 90°. Найдите угол между каждой наклон-
ной и ее проекцией.

а) 90°; б) 60°; в) 30º; г) 45°;

д) определить нельзя.

6. Отрезок, длина которого равна 10 см, пересе-
кает плоскость. Его концы находятся соответствен-
но на расстоянии 3 см и 2 см от плоскости. Най-
дите угол между данным отрезком и плоскостью.

а) 30º; б) 45°; в) определить нельзя; г) 60°; д) 90°.

7. Из точки А кплоскости α проведены две
наклонные, одна длиннее другой на 1 см. Проек-
ции наклонных равны 5 см и 2 см. Найдите
расстояние от точки А до плоскости α.

а) 10 см; б) 5 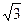см; в) 5 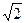см;

г) 5 см; д) 4 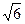см.

8. Прямая CD перпендикулярна к плоскости
остроугольного треугольника ABC, у которого СК —
высота. Найдите расстояние от точки А до пло-
скости CDK, если D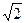A= см, a 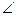DAK =45°.

а) 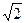см; б) 2 см; в) 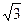см;

г) 1 см; д) 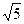см.

9. Точка М удалена от плоскости треугольника
ABC на расстояние, равное 12, и находится на
одинаковом расстоянии от его вершин. Найдите
угол между прямой МА и плоскостью ABC, если
АС = СВ = 8, 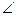ACB = 120°.

a) arccos 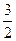; б) arcsin 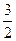; в) arctg ;

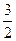г) arcctg 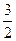; д) arcsin .

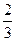10. В основании тетраэдра КМРН лежит треугольник МРН с углом H, равным 90°. Прямая НК перпендикулярна к плоскости основания. Найдите расстояние от точки K до прямой МР, если КН = 9 см, РН = 24 см, 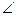MPH = 30°.

а) 9 см; б) 12 см; в) 15 см; г) 18 см; д)24см.