Перпендикулярность прямой и плоскости

Тест № 6

Перпендикулярность прямой и плоскости

I вариант

1. Какое из следующих утверждений неверно?

а) Если одна из двух параллельных прямых пер-
пендикулярна третьей прямой, то и другая прямая
перпендикулярна к этой прямой;

б) прямая называется параллельной плоскости,
если она перпендикулярна к любой прямой, лежа-
шей в этой плоскости;

в) две прямые, перпендикулярные к плоскости,
параллельны;

г) если одна из двух параллельных прямых пер-
пендикулярна к плоскости, то и другая прямая пер-
пендикулярна к этой плоскости;

д) через любую точку пространства проходит
прямая, перпендикулярная к данной плоскости, и
притом только одна.

2. Две скрещивающиеся прямые взаимно перпен-
дикулярны. Чему равен угол между ними?

а) 90°; б) 0°; в) 180°; г)45°; д) определить нельзя.

3. Через вершину квадрата ABCD проведена
прямая AM, перпендикулярная его плоскости.
Какое из следующих утверждений неверно?

a) MA 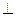BD; б) M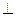D CD;

в) MB 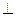ВС; г) MС 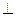ВС; д) МА 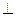АС.

4. Дан правильный треугольник ABC со стороной,
равной 3. Точка О — центр треугольника, ОМ —
перпендикуляр к его плоскости, ОМ= 1. Найдите
расстояния от точки M до вершин треугольника.

а) 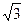; б) определить нельзя; в) 3; г) 1; д) 2.

5. Прямая т перпендикулярна к прямым а и
b, лежащим в плоскости α, но т не перпенди-
кулярна к плоскости α. Выясните взаимное рас
положение прямых а и b.

а) Параллельны; б) пересекаются;

в) скрещиваются; г) совпадают;
д) определить нельзя.

6. Отрезок АВ, равный 5 см, не имеет общих
точек с плоскостью α. Прямые АС и BD, пер
пендикулярные к этой плоскости, пересекают ее в
точках С и D соответственно. Найдите BD, если
CD = 3 см, АС= 17 см, BD < АС.

а) Определить нельзя; б) 12 см; в) 13 см;

г) 17- 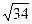см; д) 1 см.

7. Прямая перпендикулярна к двум плоскостям,
тогда плоскости:

а) пересекаются; б) параллельны;

в) определить нельзя; г) скрещиваются;

д) совпадают.

8. В тетраэдре DABC AD 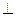AC, AD 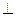AB, DC 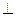ВС. Тогда прямая ВС и плоскость ADC:

а) параллельны;

б) прямая лежит в плоскости;

в) прямая пересекает плоскость, но не перпен-
дикулярна к плоскости;

г) прямая перпендикулярна к плоскости, но не
пересекает плоскость;

д) перпендикулярны.

9. Расстояние от некоторой точки до плоскости
квадрата равно 4 см, а до каждой из его вершин —
6 см. Найдите диагональ квадрата.

а) 2 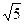см; б) 5 см; в) 5 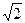см;

г) 2 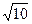см; д) 4 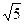см.

10. Отрезок АВ пересекает некоторую плос- кость в точке О. Прямые AD и ВС ,перпендику- лярные к этой плоскости, пересекают ее в точках D и С соответственно. Найдите длину АВ, если AD = 6 см, ВС= 2 см, ОС = 1,5 см.

а) 8 см;

б) определить нельзя;

в) 14 см; г) 9 см; д) 12 см.