Центр – точка пересечения биссектрис.

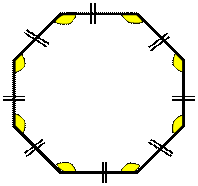Правильные многоугольники

Правильным многоугольником называется

выпуклый многоугольник, у которого все углы

и все стороны равны.

Сумма углов выпуклого n–угольника равна (n – 2) · 180˚.

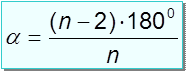- градусная мера угла правильного n –угольника

* Теорема 1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

Центр – точка пересечения биссектрис.

* Теорема 2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Центр – точка пересечения серединных перпендикуляров

* Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

* Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

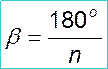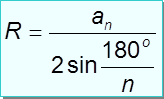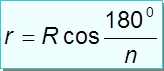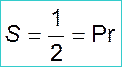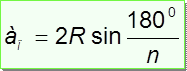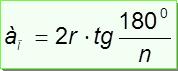Решение задач

--------------------------------------------------------------------------------------

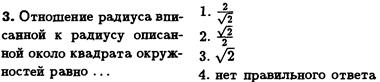
Ответы

Верные утверждения

1._______________

2.________________

3.________________

4.________________

Задачи

1.________________

2.________________

3.________________

4.________________

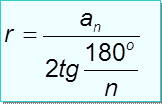
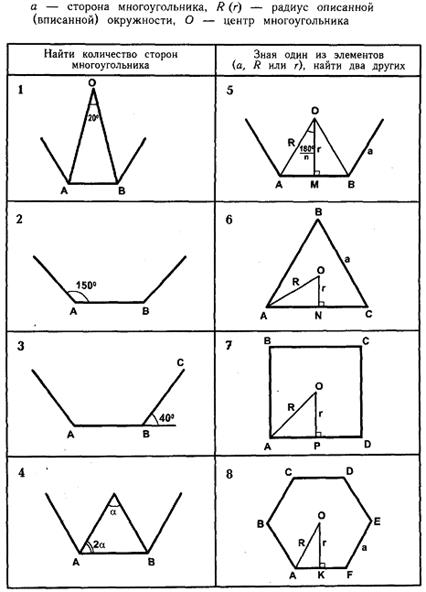
5. Если дано а_n, тогда

R_n =

r_n =

Если дано R_n, тогда

а_n =

r_n =

Если дано r_n, тогда

R_n =

а_n =

6. Если дано а₃, тогда

R₃ =

r ₃=

Если дано R₃, тогда

а_n =

r₃ =

Если дано r₃, тогда

R₃ =

а_n =

7. Если дано а₄, тогда

R₄ =

r₄ =

Если дано R₄, тогда

a₄ =

r₄ =

Если дано r₄, тогда

R₄ =

a₄ =