Контакты

Случайная статья

Тема: Решение тригонометрических уравнений

Стр 1 из 2Следующая ⇒

Тема: Решение тригонометрических уравнений

Дата: 02.03.2021 г.

Группа: ПК-261

Цели урока:

Образовательные:

o углубление понимания методов решения тригонометрических уравнений;

o сформировать навыки различать, правильно отбирать способы решения тригонометрических уравнений.

Воспитательные:

o воспитание познавательного интереса к учебному процессу;

o формирование умения анализировать поставленную задачу;

o способствовать улучшению психологического климата в классе.

Развивающие:

o способствовать развитию навыка самостоятельного приобретения знаний;

o способствовать умению учащихся аргументировать свою точку зрения;

Ход урока.

1. Актуализация опорных знаний.

Устно решить уравнения:

1) cosx = 1;

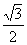2) 2 cosx = 1;

3) cosx = – ;

4) sin2x = 0;

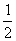
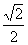5) sinx = – ;

6) sinx =

7) tgx = ;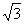

8) cos²x – sin²x = 0

Ответы:

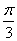1) х = 2πк;

2) х = ± +2πк;

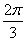3) х =± +2πк;

4) х = 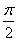к;

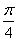
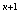
5) х = (–1) + πк;

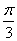
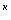
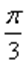6) х = (–1) +2πк;

7) х = + πк ;

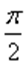
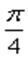
8) х = + к; к ϵ Z.

2.Решение задач

№1

Решение уравнений разложением на множители

sin 4x = 3 cos 2x

Для решения уравнения воспользуемся формулой синуса двойного угла

sin 2α = 2 sinα cosα

2 sin 2x cos 2x – 3 cos 2x = 0,

cos 2x (2 sin 2x – 3) = 0. Произведение этих множителей равно нулю, если хотя бы один из множителей будет равен нулю.

2x = 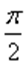+ πк, к ϵ Z или sin 2x = 1,5 – нет решений, т.к | sinα| 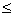1

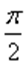x = 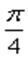+ к; к ϵ Z.

Ответ:

№2Решение уравнений преобразованием суммы или разности тригонометрических функций в произведение

cos 3x + sin 2x – sin 4x = 0.

Для решения уравнения воспользуемся формулой 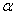sin – sin 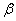= 2 sin 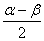сos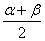

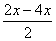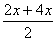cos 3x + 2 sin сos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. Полученное уравнение равносильно совокупности двух уравнений

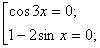
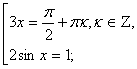
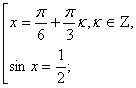
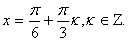Множество решений второго уравнения полностью входит во множество решений первого уравнения. Значит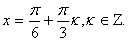

Ответ:

№3Решение уравнений преобразованием произведения тригонометрических функций в суммуsin 5x cos 3x = sin 6x cos2x.

Для решения уравнения воспользуемся формулой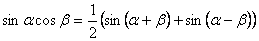

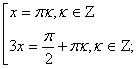
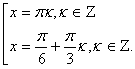
Ответ: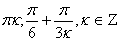

№4Решение уравнений, сводящихся к квадратным уравнениям

3 sin x – 2 cos²x = 0,
3 sin x – 2 (1 – sin²x ) = 0,
2 sin²x + 3 sin x – 2 = 0,

Пусть sin x = t, где | t | . Получим квадратное уравнение 2t²+ 3t – 2 = 0,

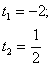D = 9 + 16 = 25.

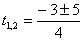. Таким образом . 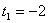не удовлетворяет условию | t | .

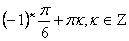
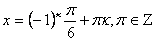Значит sin x = 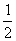. Поэтому.

Ответ:

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.