
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок 42. Задачи на построение методом подобия
Урок 42. Задачи на построение методом подобия
Цель деятельности учителя
Создать условия для применения подобия треугольников в задачах на построение
Термины и понятия
Пропорциональные отрезки, отношение, пропорции, среднее пропорциональное
I этап. Активизация знаний учащихся
Цель деятельности
Совместная деятельность
Повторение
Решить задачи на построение:
1) Постройте медиану AM треугольника ABC.
2) Постройте биссектрису МА треугольника MNK.
3) Постройте высоту РK треугольника PST.
4) Постройте прямую, параллельную стороне АВ треугольника ABC и проходящую через точку С
II этап. Решение задач на построение методом подобия
1. Разобрать задачу № 584 (деление отрезка в данном отношении). Прочитайте решение задачи по учебнику
2. Изучите внимательно решение задачи № 585 (а)
№ 585 (а). План построения:
1) Построить луч AD и отложить на нем отрезки АK и KD так, чтобы АK : KD = 2 : 5 (например, АK = 2 см, KD = 5 см).
2) Провести прямую BD.
3) Провести прямую K || BD (F 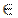 АВ). AF : FB = AK : KD = 2 : 5.
АВ). AF : FB = AK : KD = 2 : 5.
3. Прочитать самостоятельно п. 66 (задачу 3).
4. Решить самостоятельно задачу № 586.
Построение:
1) Построить угол, равный данному (ÐA).
2) Построить биссектрису данного угла и отложить на ней отрезок (АО), равный биссектрисе данного треугольника.
3) Построить угол, равный второму углу, (ÐВ1) от произвольной точки на одной из сторон первого угла
4) Через точку О провести прямую, параллельную О1В1.
5) Прямая ОВ пересекается со второй стороной угла в точке С. ∆АВС – искомый.
5. № 589.
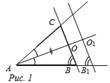
| Дано: ÐA = α, BC = a, AB : AC = 2 : 1 (рис. а). Построить: ∆АВС. | |
| Построение (рис. б): | 1) Построить ÐА = α. 2) Построить отрезки АС1 и АВ1 на сторонах ÐА так, что АВ1 : АС1 = 2 : 1. 3) Откладываем отрезок АВ = 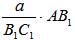 , АС = , АС = 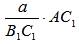 .
4) ∆АВС – искомый .
4) ∆АВС – искомый
|
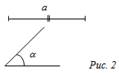
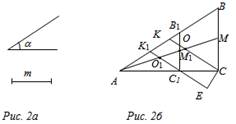
Задача: Построить треугольник ABC по углу А, отношению сторон АВ : АС = 2 : 1 и расстоянию от точки пересечения медиан до вершины С.
Дано: ÐA = α, О – точка пересечения медиан ∆АВС, ОС = m, АВ : АС = 2 : 1.
Построить: ∆АВС.
Построение: а) Построить угол А, равный α.
б) На сторонах угла А отложить отрезки АС1 и АВ1 так, что АВ1 : AС1 = 2 : 1.
в) Построить точку пересечения медиан треугольника АВ1С1 – точку О1.
г) На луче О1С1 отложить отрезок О1Е, равный m.
д) Построить прямую ЕС, параллельную медиане АМ1 треугольника АВ1С1, С = ЕС ∩ АС1.
е) Через точку С провести прямую СВ, параллельную С1В1, СВ ∩ АВ1 = В. Треугольник ABC – искомый.
 2. Построить отрезок
2. Построить отрезок 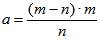 , если отрезки m и n известны.
, если отрезки m и n известны.
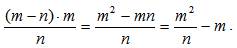 В прямоугольном ∆АВС ВD – высота, проведенная из вершины прямого угла, поэтому ВD =
В прямоугольном ∆АВС ВD – высота, проведенная из вершины прямого угла, поэтому ВD = 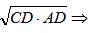 ВD2 = СD ∙ АD Þ СD = ВD2 : АD = m2 : n; DK = СD – СK. Если СK = m, то DK = m2 : n – m.
ВD2 = СD ∙ АD Þ СD = ВD2 : АD = m2 : n; DK = СD – СK. Если СK = m, то DK = m2 : n – m.
Построение:
а) Построить ∆ABD, в котором ÐD = 90°, BD = m, AD = n.
б) Провести прямую ВС так, что ВС ^ AD = С.
в) На луче СА отложить отрезок СK, равный m.
г) DK – искомый отрезок. Задача не имеет решения, если m < n
Домашнее задание: