Магнитный диполь

Стр 1 из 2Следующая ⇒

Магнитный диполь

Магнитное поле в вакууме

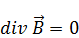
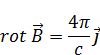
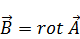
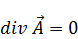
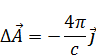
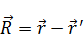
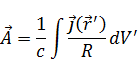
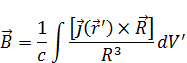
Подводка к решению. Принцип решения возвратного интеграла:

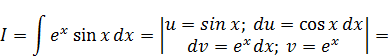
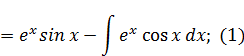
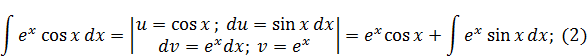
Подставим (2) в (1), получим:

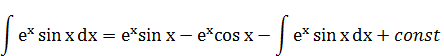
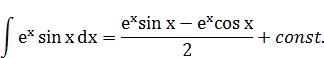
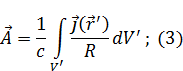
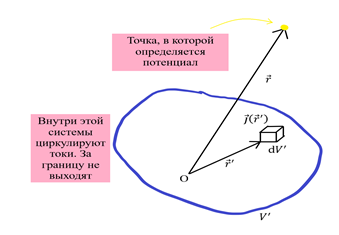
Из всей системы токов можно выбрать элементарные трубочки.

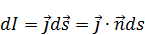
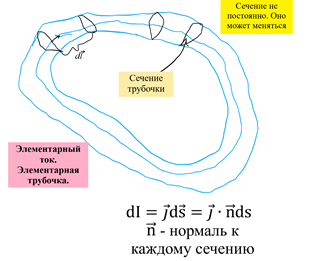
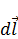– элемент траектории.

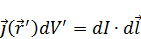
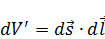
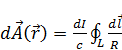- векторный потенциал, создаваемый элементарным током.

Интегрируя по всем траекториям, по всем элементарным токам, получаем формулу .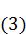

Аналогично, .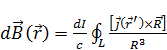

Можно перейти от 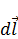к :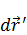

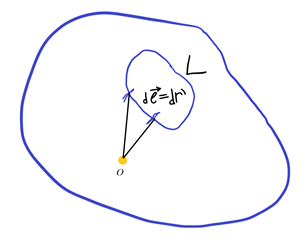
Мы рассматриваем магнитное поле, создаваемое системой токов, но на большом расстоянии.

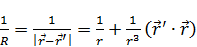– разложение в ряд Тейлора.

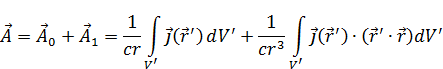
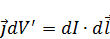
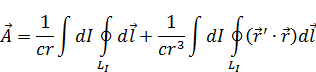
Интеграл по замкнутой траектории 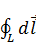равен нулю (суммируя вектора, получаем нуль) или интеграл по замкнутой траектории от полного дифференциала всегда равен нулю. В итоге :

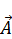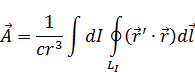
Перейдем от 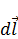к :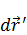

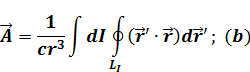
Вычислим :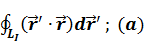

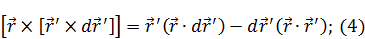
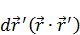- стоит под интегралом. Выразим его из (4):

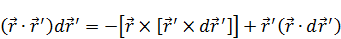
Учитывая, что 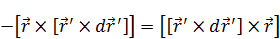, получим:

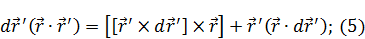
Найдем дифференциал 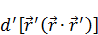(дифференциал от штрихованной системы):

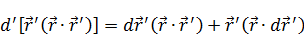
Выразим :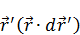

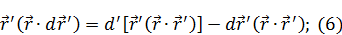
Подставим (6) в (5):

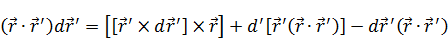
Перенеся 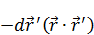влево, приведем подобные слагаемые, далее поделим на 2:

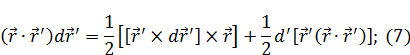
Подставим (7) в (a):

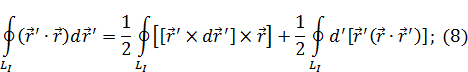
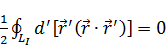– интеграл от полного дифференциала всегда равен нулю.

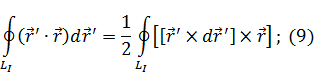
Подставим (9) в (b):

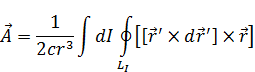
Перейдем обратно:

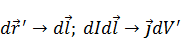
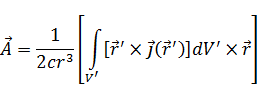
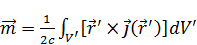- момент.

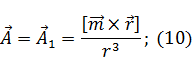
Найдем вектор магнитного поля через формулу :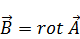

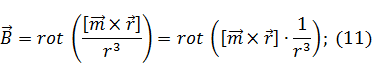
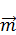– постоянный.

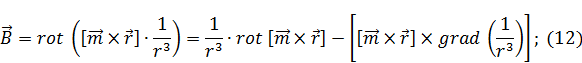
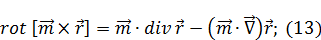
Зная, что 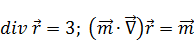, выражение (13) примет вид:

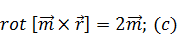
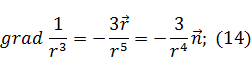
В выражении (12) раскроем двойное векторное произведение:
:

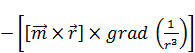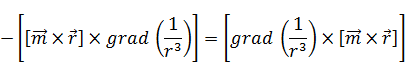
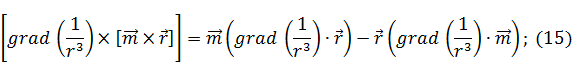
Учитывая (14) в (15):

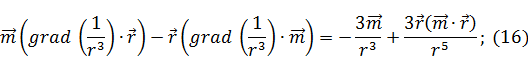
В итоге:

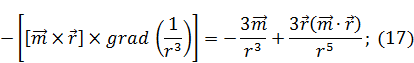
Подставляя (17) в (12) и учитывая (c), получим:

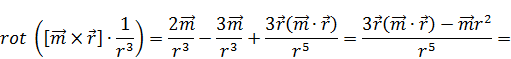
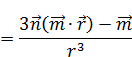
В итоге находим выражение для вектора магнитного поля:

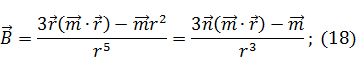
Аналогия с электричеством: выражения для 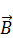совпадает по форме с выражением для 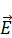. Выражение совпадает с полем электрического диполя. Силовые линии магнитного диполя идентичны силовым линиям электрического диполя.

Сила и момент сил, действующие на диполь

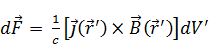– сила, действующая на элемент тока

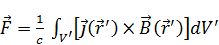- сила, действующая на систему токов

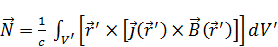- момент сил, действующие на систему токов

Разложение в ряд Тейлора (приближение 1-го порядка):

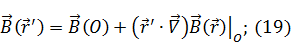
Подставим (19) в силу, действующую на систему токов:

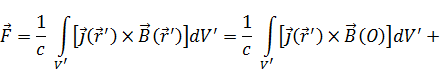
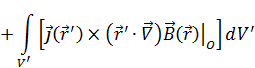
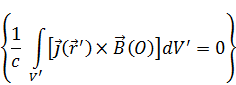
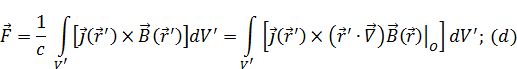
Выражение 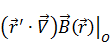встречается в градиенте:

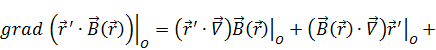
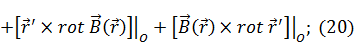
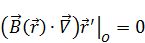– набла идет по нештрихованной системе, поэтому нуль.

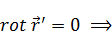
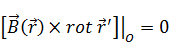
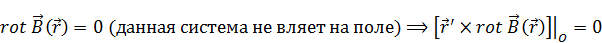
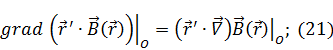
Подставим (21) в (d):

12 Следующая ⇒