
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вопросы и ответы по кинематике
Вопросы и ответы по кинематике
Какие кинематические способы задания движения точки существуют и в чем состоит каждый из этих способов?
Существуют: естественный, векторный и координатный способы задания движения точки.
а). Естественный способ задания движения применяется в случае, когда траектория точки заранее известна (прямая или кривая линия). Положение движущейся точки на траектории определяется дуговой координатой, отсчитываемой от начала отсчёта:
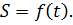
б). При векторном способе задания движения положения точки в пространстве определяется заданием радиус-вектора 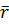 , проведённого из неподвижного центра в данную точку.
, проведённого из неподвижного центра в данную точку.
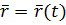
в). При координатном способе задания движения положение точки в декартовой системе координат 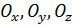 определяется тремя координатами.
определяется тремя координатами.
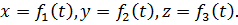
Чем является траектория точки при векторном способе задания движения точки?
Траектория точки является годографом её радиус-вектора 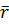 .
.
Как по уравнениям движения точки в координатной форме определить её траекторию?
Для получения уравнения траектории необходимо исключить из уравнений движения параметр 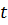 (время).
(время).
Если движения точки в плоскости задано уравнениями:
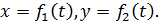
то, решив первое уравнение относительно 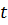 , получим
, получим 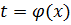 . Подставив
. Подставив 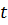 во второе уравнение, получим уравнение траектории:
во второе уравнение, получим уравнение траектории:
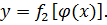
Чему равен вектор скорости точки в данный момент и какое направление он имеет?
Скорость 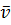 – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта. Вектор скорости равен производной от радиус вектора точки по времени:
– это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта. Вектор скорости равен производной от радиус вектора точки по времени:
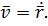
Вектор скорости точки 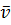 направлен по касательной к траектории в сторону движения точки.
направлен по касательной к траектории в сторону движения точки.
Как связан орт касательной к кривой с радиус-вектором движущейся точки?
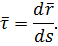
Чему равна проекция скорости точки на касательную к её траектории и модуль её скорости?
Производная от дуговой координаты по времени 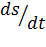 представляет собой проекцию вектора скорости
представляет собой проекцию вектора скорости 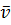 на касательную к траектории:
на касательную к траектории:
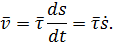
Модуль скорости точки равен абсолютному значению производной от дуговой координаты точки по времени 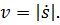
Как определяются проекции скорости точки на неподвижные оси декартовой системы координат?
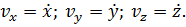
Как определяется величина и направление вектора скорости при координатном способе задания движения точки?
Величина вектора скорости определяется направляющими косинусами:
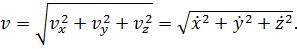
Направления вектора скорости определяется направляющими косинусами:
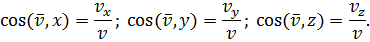
Чему равен вектор ускорения точки и как он направлен по отношения к годографу скорости?
Ускорение 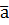 – это векторная величина, характеризующая быстроту изменения модуля и направления скорости точки.
– это векторная величина, характеризующая быстроту изменения модуля и направления скорости точки.
Вектор ускорения точки равен первой производной от скорости или второй производной от радиус-вектора точки по времени.
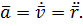
Как направлены естественные координатные оси в каждой точке кривой?
Естественными координатными осями называются три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты, главная нормаль, направленная в сторону вогнутости кривой и бинормаль, направленная перпендикулярно плоскости проведённой через касательную и главную нормаль.
В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?
Вектор ускорения точки 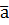 лежит в соприкасающейся плоскости и равен геометрической сумме двух вектором, один из которых направленный по главной нормали, называется нормальным ускорением, а другой, направлен по касательной, называется касательным ускорением.
лежит в соприкасающейся плоскости и равен геометрической сумме двух вектором, один из которых направленный по главной нормали, называется нормальным ускорением, а другой, направлен по касательной, называется касательным ускорением.
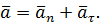
Проекция ускорения на главную нормаль равна квадрату модуля скорости точки на радиус кривизны.
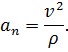
Проекция ускорения на касательную равна первой производной от алгебраической величины скорости или второй производной от дуговой координаты по времени
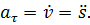
Как определяется величина и направление ускорения точки при естественном способе задания движения?
Величина ускорения равна:
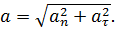
Направление ускорения определяется углом 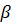 между вектором
между вектором 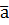 и главной нормалью:
и главной нормалью:
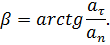
Что характеризует собой касательное ускорение?
Касательное ускорение существует лишь при неравномерном движении и характеризует изменение скорости по величине.
При каком движении точки равно нулю касательное ускорение, и при каком – нормальное?
Касательное ускорение равно нулю ( 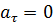 ), при равномерном движении точки.
), при равномерном движении точки.
Нормальное ускорение равно нулю ( 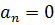 ), в случае прямолинейного движения точки.
), в случае прямолинейного движения точки.
Как классифицируются движения точки по ускорениям?
Если во всё время движения касательное ускорение равно нулю 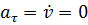 , то движение называется равномерным.
, то движение называется равномерным.
Если касательное ускорение точки во всё время движения постоянно 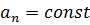 , то движение называется равнопеременным.
, то движение называется равнопеременным.
Как определяются проекции ускорения на неподвижные оси декартовых координат?
Проекции ускорения на неподвижные оси равны первым производным по времени от проекций скоростей на соответствующие оси или вторым производным от соответствующих координат точки:
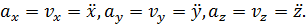
Как определяется модуль и направление ускорения при координатном способе задания движения точки?
Модуль ускорения определяется через проекции:
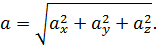
Направление ускорения 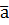 определяется направляющими косинусами:
определяется направляющими косинусами:
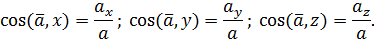
Что характеризует собой нормальное ускорение?
Нормальное ускорение существует лишь при криволинейном движении и характеризует изменение направления скорости.
В какие моменты времени нормальное ускорение в криволинейном движении может обратиться в нуль?
Нормальное ускорение в данный момент времени может быть равно нулю 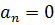 в том случае, когда в данный момент скорость точки обращается в нуль (точка меняет направление движения), или, когда движущаяся точка находится в точке перегиба своей траектории
в том случае, когда в данный момент скорость точки обращается в нуль (точка меняет направление движения), или, когда движущаяся точка находится в точке перегиба своей траектории 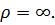
В какие моменты времени касательное ускорение в неравномерном движении может обратиться в нуль?
Если в данный момент времени 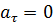 , то в этот момент величина скорости достигает максимума или минимума.
, то в этот момент величина скорости достигает максимума или минимума.
Если 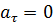 в течение некоторого промежутка времени, то на этом интервале времени численная величина скорости постоянна и движение является равномерным криволинейным, а ускорение направлено по главной нормали.
в течение некоторого промежутка времени, то на этом интервале времени численная величина скорости постоянна и движение является равномерным криволинейным, а ускорение направлено по главной нормали.
Чем отличается график пути от графика движения точки?
Графиком движения точки называется график зависимости её дуговой координаты 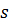 от времени
от времени 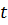 .
.
Путь, пройденный точкой за некоторый промежуток времени, представляет собой сумму абсолютных значений элементарных перемещений за этот промежуток времени, т.е. линия этого графика непрерывно поднимается вверх независимо от направления движения.
Как по графику движения определить алгебраическую величину скорости точки?
Для определения скорости точки в любой момент времени следует провести касательную к графику движения в соответствующей точке, определить угол 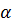 наклона этой касательной к оси
наклона этой касательной к оси 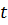 и определить скорость
и определить скорость
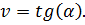
Как по графику скорости определить алгебраическую величину касательного ускорения точки?
Для определения касательного ускорения точки следует провести касательную к графику скорости в соответствующей точке и найти угол наклона 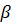 этой касательной к оси
этой касательной к оси 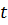 . Тангенс угла
. Тангенс угла 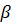 определяет алгебраическую величину касательного ускорения:
определяет алгебраическую величину касательного ускорения:
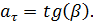
В каком случае полное ускорение точки в течение некоторого промежутка времени может быть равно нулю.
Полное ускорение может быть равно нулю 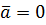 , когда точка движется относительно выбранной системы отсчёта равномерно и прямолинейно.
, когда точка движется относительно выбранной системы отсчёта равномерно и прямолинейно.
Назовите основные виды движения твёрдого тела.
Различают пять видов движения твёрдого тела: поступательное, вращательное, плоскопараллельное (плоское), сферическое и общий случай движения твёрдого тела.
Какое движение твёрдого тела называется поступательным?
Поступательным движением твёрдого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Все точки твёрдого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Какое движение твёрдого тела называется вращательным?
Вращательным называется такое движение твёрдого тела, при котором остаются неподвижными все его точки, лежащие на прямой называемой осью вращения.
При этом все остальные точки движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси.
Как определяется положение вращающегося тела?
Положение вращающегося тела в любой момент времени определяется углом поворота 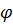 , являющегося функцией времени
, являющегося функцией времени 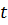 .
.
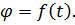
Это уравнение представляет собой уравнение вращательного движения тела.
Какая величина называется угловой скоростью?
Величина, характеризующая быстроту изменения угла поворота 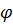 с течением времени, называется угловой скоростью тела
с течением времени, называется угловой скоростью тела
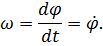
Какая величина называется угловым ускорением?
Алгебраическая величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела
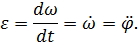
Какое вращение называется равномерным?
Если во всё время движения 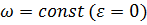 , то вращение называется равномерным.
, то вращение называется равномерным.
Какое вращение называется равнопеременным?
Вращение тела, при котором угловой ускорение постоянно 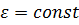 , называют равнопеременным вращением. При этом если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренными, а если уменьшается – равнозамедленным
, называют равнопеременным вращением. При этом если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренными, а если уменьшается – равнозамедленным
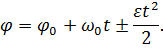
Каким образом характеризуется вращение твёрдого тела векторами 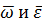 ?
?
Состояние движения вращающегося твёрдого тела в данный момент характеризуется вектором 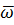 , направленным по оси вращения в ту сторону, откуда вращение представляется происходящим против часовой стрелки.
, направленным по оси вращения в ту сторону, откуда вращение представляется происходящим против часовой стрелки.
Угловое ускорение вращающегося твёрдого тела модно изобразить в виде вектора 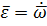 , направленного вдоль оси вращения. При этом направление
, направленного вдоль оси вращения. При этом направление 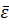 совпадает с направлением
совпадает с направлением 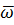 , когда тело вращается ускоренно, и противоположно
, когда тело вращается ускоренно, и противоположно 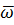 , когда вращение является замедленным.
, когда вращение является замедленным.
Как определяется скорость точки вращающегося тела?
Модуль вращательной скорости точки твёрдого тела равен произведению кратчайшего расстояния от точки до оси вращения изугловую скорость тела:
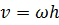
Век гор вращательной скорости 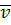 направлен перпендикулярно радиусу в сторону вращения.
направлен перпендикулярно радиусу в сторону вращения.
Как определяется вектор скорости 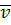 при помощи формулы Эйлера?
при помощи формулы Эйлера?
Вращательная скорость точки равна векторному произведению вектора угловой скорости тела на радиус-вектор этой точки относительно оси вращения:
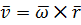
Как определяются проекции скорости точки на оси координат по формулам Эйлера, если осью вращения является ось z?
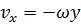 ,
, 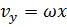 ,
, 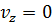 ,
,
где 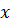 ,
, 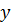 – координаты точки.
– координаты точки.
Как определяется ускорение точки вращающегося твёрдого тела?
Ускорение точки вращающегося твёрдого тела равно геометрической сумме нормального и касательного ускорений:
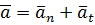
Как определяются величины нормального и касательного ускорении точки вращают тела?
Модуль нормального ускорения равен произведению кратчайшего расстояния (радиуса) от точки до оси вращения на квадрат полной угловой скорости тела:
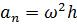
Модуль касательного ускорения равен произведению кратчайшего расстояния (радиуса) от точки до оси вращения на абсолютное значение углового ускорения тела:
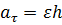
Как определяется величина полного ускорения точки прощающегося твёрдого тела?
Модуль полного ускорения точки определяется по формуле:
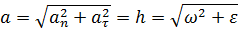
Направление определяется утлом 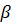 , составленным полным ускорением
, составленным полным ускорением 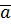 с радиусом окружности, тангенс которого:
с радиусом окружности, тангенс которого:
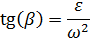
При равномерном вращении 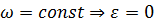 :
:
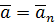
В этом случае ускорение 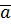 направлено по радиусу к центру окружности, описываемой точкой.
направлено по радиусу к центру окружности, описываемой точкой.
Как определяются векторы касательного 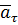 . и нормального
. и нормального 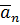 ускорений?
ускорений?
Касательное ускорение точки вращающегося твёрдого тела равно векторному произведению вектора углового ускорения тела на радиус-вектор этой точки относительно оси вращения:
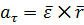
Нормальное ускорение точки вращающегося твёрдого тела равно векторному произведению вектора угловой скорости тела на вращательную скорость этой точки:
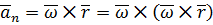
Как вычисляются проекции ускорения точки тела, вращающегося вокруг оси 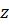 ?
?
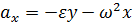 ,
, 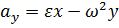 ,
, 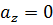 .
.
Какое движение твёрдого тела называется плоским?
Плоскопараллельным (или плоским) движением твёрдого тела называется такое движение, при котором все точки тела движутся параллельно неподвижной (основной) плоскости.
Назовите основные виды движения плоской фигуры.
Положение плоской фигуры определяется тремя параметрами: координатами полюса 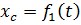 ,
, 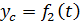 и углом поворота относительно полюса
и углом поворота относительно полюса 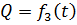 .
.
Основными видами движения плоской фигуры являются поступательное движение вместе с полюсом 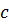 и вращательное движение относительно полюса. Причём, поступательное движение зависит от выбора полюса, а вращательное от выбора полюса не зависит.
и вращательное движение относительно полюса. Причём, поступательное движение зависит от выбора полюса, а вращательное от выбора полюса не зависит.
Как определяется скорость любой точки плоской фигуры при разложения плоского движения на поступательное и вращательное?
Скорость любой точки плоской фигуры равна геометрическойсумме скорости полюса 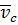 и вращательной скорости этой точки относительно полюса
и вращательной скорости этой точки относительно полюса 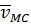 :
:
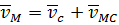
Вектор 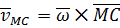 перпендикуляренпрямой
перпендикуляренпрямой 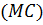 ,соединяющей точку
,соединяющей точку 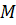 с полюсом
с полюсом 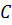 .
.
Скорость точки изображается диагональю параллелограмма, построенного при точке на скорости полюса, перенесённой в точку, и вращательной скорости точки вокруг полюса.
Назовите следствия из теоремы о скоростях точек плоской фигуры.
Следствие 1. Проекции скоростей точек плоской фигуры на прямую их соединяющую равны между собой.
Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками.
Какую точку плоской фигуры называют мгновенным центром скоростей?
Точка 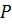 плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС). Мгновенный центр скоростей плоской фигуры находится на перпендикуляре к направлению скорости точки
плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС). Мгновенный центр скоростей плоской фигуры находится на перпендикуляре к направлению скорости точки 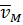 , на расстоянии от точки, равном
, на расстоянии от точки, равном 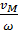 .
.
Как определяются скорости точек плоской фигуры при помощи мгновенного центра скоростей?
Скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей:
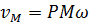 ,
, 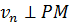 ,
,
т.е. скорость любой точки плоской фигуры имеет модуль, равный произведению мгновенной угловой скорости фигуры на длину отрезка, соединяющего точку с мгновенным центром скоростей, и направлена перпендикулярно этому отрезку в сторону вращения фигуры.
Модули скоростей точек плоской фигуры в каждый момент времени пропорциональны расстояниям от этих точек до мгновенного центра скоростей:
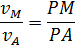
Сформулируйте теорему Шаля.
Плоскую фигуру можно переместить из одного положения в любое другое положение на плоскости одним поворотом этой фигуры вокруг некоторого неподвижного центра.
Предельным положением центра поворота является точка неподвижной плоскости, с которой в данный момент совпадает мгновенный центр скоростей плоской фигуры. Эта точка называется мгновенным центром вращения фигуры.
Что представляет собой неподвижная и подвижная центроиды и что происходит с центрами при действительном движении плоской фигуры?
Кривая, представляющая геометрическое место мгновенных центров вращения на неподвижной плоскости, называется неподвижной центроидой.
Кривая, представляющая геометрическое место мгновенных центров скоростей, неизменно связанная с подвижной плоской фигурой, называется подвижной центроидом.
При действительном движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде (теорема Пуансо).
Как определяется ускорение любой точки плоской фигуры?
Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении вокруг полюса.
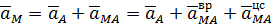
где  ,
, 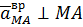 ,
, 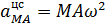 ,
, 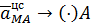 .
.
Ускорение точки 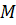 плоской фигуры определяется нулем построения
плоской фигуры определяется нулем построения
многоугольника ускорений.
Назовите следствия теоремы об ускорениях точек плоской фигуры.
Следствие 1: Проекция ускорения любой точки плоской фигуры на ось, проведённую из произвольного полюса через эту точку, не может быть больше проекции ускорения полюса на ту же ось.
Следствие 2: Концы ускорений точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между этими точками.
Какую точку плоской фигуры называют мгновенным центром ускорений, и может ли мгновенный центр ускорений совпадать с мгновенным центром скоростей?
Точка 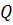 , ускорение которой в данный момент равно нулю, называется мгновенным центром ускорений (МЦУ).
, ускорение которой в данный момент равно нулю, называется мгновенным центром ускорений (МЦУ).
Мгновенный центр скоростей 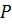 и мгновенный центр ускорений
и мгновенный центр ускорений 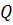 являются различными точками плоской фигуры.
являются различными точками плоской фигуры.
Перечислите известные вам способы определения положения мгновенного центра ускорений.
а)По условию задачи известна точка плоской фигуры, ускорение которой в данный момент равно нулю. Эта точка является мгновенным центром ускорений.
б)Известны модуль и направление ускорения точки плоской фигуры,алгебраические величины угловой скорости 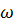 и углового ускорения
и углового ускорения 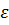 .
.
МЦУ находится на отрезке, составляющем с вектором ускорения 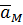 угол
угол  , который отложен от вектора ускорения точки в сторону
, который отложен от вектора ускорения точки в сторону 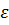 на расстоянии отточки
на расстоянии отточки 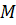 , равном:
, равном:
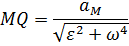
в) Известны модули и направления ускорений двух точек 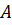 и
и 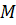 плоской фигуры.
плоской фигуры.
Примем точку 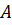 за полюс, тогда:
за полюс, тогда:
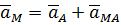
Построим при точке 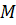 параллелограмм ускорений по заданной диагонали
параллелограмм ускорений по заданной диагонали 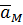 , и одной из сторон
, и одной из сторон 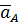 . Другая сторона параллелограмма определит ускорение
. Другая сторона параллелограмма определит ускорение 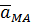 . Ускорение
. Ускорение 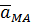 составляет угол
составляет угол  резком
резком 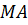 . Отложим угол
. Отложим угол 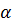 от ускорений точек
от ускорений точек 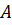 и
и 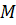 по направлению
по направлению 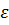 .Точка пересечения полупрямых
.Точка пересечения полупрямых 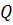 и будет мгновенным центром ускорений.
и будет мгновенным центром ускорений.
Как определяются ускорения точек плоской фигуры через мгновенный центр ускорений?
Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки с мгновенным центром ускорений, один и тот же угол  .
.
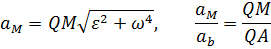
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|