
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛАБОРАТОРНАЯ РАБОТА НА ТЕМУ. Определение ускорения свободного падения на телах Солнечной системы при помощи машины Атвуда. Определение ускорения свободного падения на телах Солнечной системы при помощи машины Атвуда.. Теория.
Министерство науки и высшего образования Российской Федерации
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (ТГУ)
ЛАБОРАТОРНАЯ РАБОТА НА ТЕМУ
Определение ускорения свободного падения на телах Солнечной системы при помощи машины Атвуда
Руководитель
Абрашитов С.В
«__7__»___01____2020 г.
Студенты группы № 052001
Марлисова Каимла
Тагаева Адеми
Томск-2020
Определение ускорения свободного падения на телах Солнечной системы при помощи машины Атвуда.
Цель работы:используя установку “Машина Атвуда”, определить ускорение свободного падения тел на планетах солнечной системы.
Теория.
Рассмотрим систему, состоящую из двух грузов, подвешенных на легкой нерастяжимой нити, перекинутой через блок радиуса R. Момент инерции блока I. Если на один из грузов положить перегрузок массой m, то система придет в движение. Уравнения движения имеют вид (см. рис. 1):
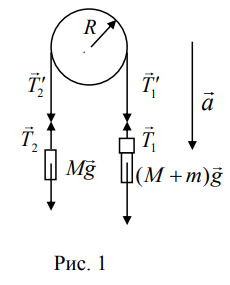
правый груз (M + m)g -T1 = (M + m)a ,
левый груз T2 - Mg = Ma, (1)
блок (T1 -T2 )R - Mтр = Ie, e = a / R,
где а – ускорение грузов, Т1 и Т2 – силы натяжения нитей, e – угловое ускорение блока, I – момент инерции блока, R – радиус блока, Mтр – момент силы трения. Решая систему уравнений (1) относительно ускорения грузов, получим:
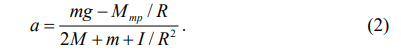

Отсюда видно, что ускорение грузов линейно зависит от массы перегрузка m. Таким образом, построив по экспериментальным данным прямую зависимости a от m, можно найти ускорение свободного падения из углового коэффициента наклона этой прямой.
Тангенс угла наклона прямой a = f (m) равен
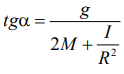
Отсюда:
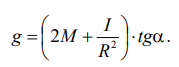
Кроме того, можно найти момент силы трения. Если продолжить прямую a = f (m) до пересечения с осью ускорений, то отрезок, отсекаемый графиком по оси ординат равен
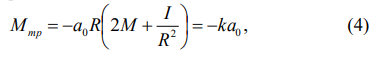
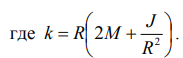
Зная величину k и найдя из график a0, найдем величину Мтр. Ускорение грузов находится по формуле a = 2h /t2, (5) где h – расстояние от начального положения нижней части правого груза до основания установки, t – время движения груза на этом пути.
Момент инерции блока можно рассчитать следующим образом. Блок можно представить в виде диска с вынутыми из него шестью одинаковыми маленькими дисками, расположенными на одинаковом расстоянии от оси вращения. Обозначим радиус блока через R, радиусы вынутых дисков (отверстий) через r, расстояние от их центров до оси вращения через l и через I – искомый момент инерции. Тогда по теореме Штейнера можно записать:
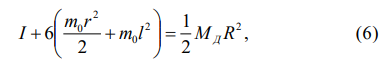
где Мд – масса диска и m0 – масса вырезанного диска. Очевидно, что масса равна

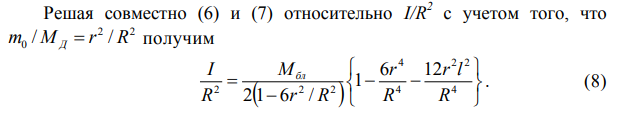
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|