Вопросы по электротехнике (16-20)

Вопросы по электротехнике (16-20)

16. Закон полного тока

Закон полного тока — один из основных законов электромагнитного поля. Устанавливает взаимосвязь между магнитной силой и величиной тока, проходящего через поверхность. Под полным током понимается алгебраическая сумма токов, пронизывающих поверхность, ограниченную замкнутым контуром. Рассмотрим плоскость, через которую перпендикулярно к ней проходит провод с током I. Напряженность H магнитного поля на расстоянии a от центра провода равна H=B/μ_a=I/(2πa), откуда ток I=Н2πa=HL. Произведение напряженности магнитного поля и длины магнитной линии L=2πa — не что иное, как магнитодвижущая сила F_м. Поверхность, ограниченную магнитной линией, пронизывает только ток I, поэтому алгебраическая сумма токов равна самому току ΣI_п=I. Отсюда ΣI_п=F_м. Это и есть аналитическое выражение закона полного тока. Намагничивающая сила вдоль контура равна полному току, проходящему сквозь поверхность, ограниченную этим контуром. В общем случае напряженность поля на различных участках магнитной линии может иметь разные значения, и тогда намагничивающая сила будет равна сумме намагничивающих сил каждой линии F_м=H₁L₁+H₂L₂+ H₃L₃+…

Рисунок:

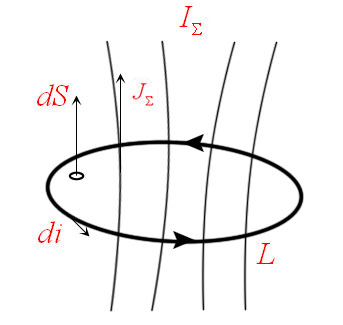
17. Явление магнитного гистерезиса.

Гистерезис (от греч. hysteresis - отставание, запаздывание), явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля). Гистерезис наблюдается в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. Неоднозначная зависимость величин наблюдается в любых процессах, т.к. для изменения состояния тела всегда требуется определённое время (время релаксации) и реакция тела отстаёт от вызывающих её причин. Такое отставание тем меньше, чем медленнее изменяются внешние условия Однако для некоторых процессов отставание при замедлении изменения внешних условий не уменьшается. В этих случаях неоднозначную зависимость величин называется гистерезисной, а само явление - Гистерезис

Гистерезис наблюдается в различных веществах и при разных физических процессах. Наибольший интерес представляют: магнитный Гистерезис, диэлектрический Гистерезис и упругий Гистерезис

Магнитный Гистерезис наблюдается в магнитных материалах, например в ферромагнетиках. Основной особенностью ферромагнетиков является наличие спонтанной (самопроизвольной) намагниченности. Обычно ферромагнетик намагничен не однородно, а разбит на домены - области однородной спонтанной намагниченности, у которых величина намагниченности (магнитного момента единицы объема) одинакова, а направления различны. Под действием внешнего магнитного поля число и размеры доменов, намагниченных по полю, увеличиваются за счёт др. доменов. Кроме того, магнитные моменты отдельных доменов могут поворачиваться по полю. В результате магнитный момент образца увеличивается.

Диэлектрический Гистерезис наблюдается обычно в сегнетоэлектриках, например титанате бария. Зависимость поляризации Р от напряжённости электрического поля Е в сегнетоэлектриках (рис. 3) подобна зависимости М от Н в ферромагнетиках и объясняется наличием спонтанной электрической поляризации, электрических доменов и трудностью перестройки доменной структуры. Гистерезисные потери составляют большую часть диэлектрических потерь в сегнетоэлектриках.

Упругий Гистерезис, т. е. гистерезисная зависимость деформации и от механического напряжения s, наблюдается в любых реальных материалах при достаточно больших напряжениях (рис. 6). Упругий Гистерезис возникает всякий раз, когда имеет место пластическая (неупругая) деформация (см. Пластичность). Пластическая деформация обусловлена перемещением дефектов, например дислокаций, всегда присутствующих в реальных материалах. Примеси, включения и др. дефекты, а также сама кристаллическая решётка стремятся удержать дислокацию в определенных положениях в кристалле. Поэтому требуются напряжения достаточной величины, чтобы сдвинуть дислокацию. Механическая обработка и введение примесей приводят к закреплению дислокаций, в результате чего происходит упрочнение материала, пластическая деформация и упругий Гистерезис наблюдаются при больших напряжениях. Энергия, теряемая в образце за один цикл, идёт в конечном счёте на нагревание образца. Потери на упругий Гистерезис дают вклад во внутреннее трение. В случае упругих деформаций, помимо гистерезисных, есть и др. потери, например обусловленные вязкостью. Величина этих потерь, в отличие от гистерезисных, зависит от частоты изменения s (или и). Иногда понятие «упругий Гистерезис» употребляется шире - говорят о динамической петле упругого Гистерезис, включающей все потери на данной частоте.

18. Магнитная цепь. Магнитная проницаемость.

Магнитная цепь — последовательность взаимосвязанных магнетиков, по которым проходит магнитный поток.^[1]

При расчётах магнитных цепей используется почти полная формальная аналогия с электрическими цепями.

В схожем математическом аппарате также присутствует закон Ома, правила Кирхгофа и другие термины и закономерности.^[2]

Магнитная цепь и сопутствующий математический аппарат используется для расчётов трансформаторов, электрических машин, магнитных усилителей и т. п.

В зависимости от источника магнитного потока магнитные цепи подразделяют^[1] на поляризованные и нейтральные. В отличие от нейтральных, поляризованные магнитные цепи содержат постоянные магниты.^[1]

Направление магнитных линий и направление создающего их тока связаны между собой известным правилом правоходового винта (буравчика) (рис. 4.1).

Основной величиной, характеризующей интенсивность и направление магнитного поля является – вектор магнитной индукции 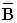, которая измеряется в Теслах [Тл].

Вектор 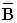направлен по касательной к магнитной линии, направление вектора совпадает с осью магнитной стрелки, помещенной в рассматриваемую точку магнитного поля.

Величина 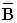определяется по механической силе, действующей на элемент проводника с током, помещенный в магнитное поле.

Если 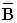во всех точках поля имеет одинаковую величину и направление, то такое поле называется равномерным.

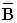зависит не только от величины I, но и от магнитных свойств окружающей среды.

Второй важной величиной, характеризующей магнитное поле является – магнитный поток 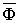, который измеряется в Веберах [Вб].

Элементарным магнитным потоком Ф сквозь бесконечно малую площадку называется величина (рис. 4.2)

dФ = B cos α dS,

где α – угол между направлением 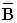и нормалью 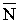к площадке dS.

Магнитная проницаемость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией 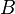и напряжённостью магнитного поля 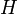в веществе. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая ее состав, состояние, температуру и т. д.).

В общем связь соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как

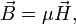
и 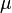в общем случае здесь следует понимать как тензор, что в компонентной записи соответствует^[2]:

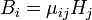
Вообще говоря магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля (а кроме того от температуры^[3], давления итд).

Также зависит от характера изменения поля со временем, в частности, для синусоидального колебания поля — зависит от частоты этого колебания (в этом случае вводят комплексную магнитную проницаемость чтобы описать влияние среды на сдвиг фазы 'B' по отношению к 'H'). При достаточно низких частотах (небольшой быстроте изменения поля) ее можно обычно считать в этом смысле константой.

· Магнитная проницаемость сильно зависит от величины поля для нелинейных сред (типичный пример — ферромагнетики, для которых характерен гистерезис). Для таких сред магнитная проницаемость как независящее от поля число может указываться приближенно, в рамках линеаризации^[4].

· Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо для широкого диапазона величин поля.

19. Закон магнитной цепи. Закон полного тока в неоднородной магнитной цепи.

Расчеты магнитных цепей основываются на законе полного тока

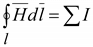(5.2)

и на принципе непрерывности магнитного потока

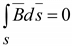. (5.3)

Согласно закона полного тока линейный интеграл вектора напряженности магнитного потока Н вдоль произвольного контура l равен алгебраической сумме токов, пронизывающих этот контур.

Линейный интеграл напряженности характеризует намагничивающее действие электрического тока и называется намагничивающей силой (НС) или магнитодвижущей силой (МДС) вдоль данного замкнутого контура. В уравнении (5.2) направление тока и направление обхода контура связаны друг с другом правовинтовой системой.

Поток вектора магнитной индукции В через некоторую поверхность s называют магнитным потоком

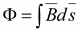.(5.4)

Принцип непрерывности (5.3) говорит о том, что магнитный поток через произвольную замкнутую поверхность равен нулю, т.е. линии вектора 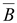или магнитные линии всегда замкнуты.

Чем больше величина магнитной проницаемости материала, тем легче проходить магнитному потоку по участку магнитной цепи, выполненному из данного материала. Максимальная проницаемость в лучших случаях имеет порядок 10⁵ ÷ 10⁶, тогда как проницаемость неферромагнитных материалов, в том числе и воздуха, практически равна единице. Таким образом, соотношение между проницаемостью участков магнитопровода и окружающей среды не превышает 10⁵ ÷ 10⁶. В электрических цепях соотношение между проводимостью участков цепи и окружающей среды составляет 10¹⁰ ÷ 10²⁰. Поэтому включение воздушного зазора в цепь не приводит к ее разрыву, т.е. магнитный поток не уменьшается до нуля.

Магнитные цепи часто содержат воздушные зазоры. Эти зазоры могут быть неизбежны по конструктивным причинам (магнитопроводы трансформаторов) или быть принципиально необходимыми (зазоры между статором и ротором электрических машин). Форма магнитного поля в воздушном зазоре обычно неоднородна и трудно поддается расчету. Только в случае, когда длина магнитных зазоров мала по сравнению с поперечными размерами, поле в воздушном зазоре можно считать однородным. В таком поле F = B×s.

20. Расчёт магнитных цепей

Это полная жопа… Как я понял, тут надо через 16 вопрос, через закон полного тока… КАК это сделать, я не возьмусь объяснить. Вот что в инете(разбор задачки)

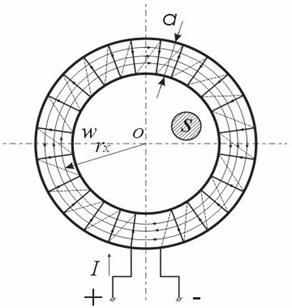
Обмотка имеет W витков и обтекается током I. Магнитные линии внутри кольца представляют собой концентрические окружности с центров точке О. Применим к контуру C_х, совпадающему с одной из магнитных линий, проходящих в магнитопроводе, закон полного тока. При этом будем считать:

1. 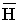и 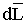совпадают, следовательно α = 0;

2. величина Нх во всех точках контура одинакова;

3. сумма токов, пронизывающих контур, равна IW.

Тогда

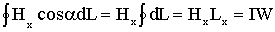Отсюда

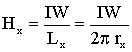[А/м],

где L_x – длина контура, вдоль которого велось интегрирование;
r_x – радиус окружности.

Вектор 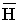внутри кольца зависит от расстояния r_х. Если α – ширина кольца << d, то эта разница между значениями Н в пределах сердечника не велика. При этом в расчет допустимо принять для всего поперечного сечения магнитопровода одно значение напряженности магнитного поля:

H_ср = IW / L ,

где L – длина средней магнитной линии.