Расширения регулярных выражений

тип 3	регулярные
	леволинейная	A®Bg \| g, где A,BÎV_N , gÎV_T^*
	праволинейная	A®gB \| g, где A,BÎV_N , gÎV_T^*.
тип 3	автоматные
	леволинейная	A®Bt \| t, где A,BÎV_N , tÎV_T
	праволинейная	A®tB \| t, где A,BÎV_N , tÎV_T

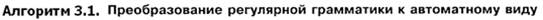
Моделировать работу ДКА значительно проще, чем НКА. Доказано, что для любого НКА можно построить эквивалентный ему ДКА. Для этого существует специальный алгоритм, идея которого состоит в следующем:

§ В качестве состояний нового ДКА рассматриваются все состояния исходного автомата, а также всевозможные сочетания этих состояний по два, по три, …, по n, если в исходном автомате было n состояний.

§ Для всех новых состояний строится функция переходов, в которой для каждого состояния q_iq_j появляется переход в новое состояние, представляющий собой объединение всех прежних переходов из q_i и q_j.

§ Начальное состояние нового автомата остается тем же, а множество конечных состояний нового автомата будут состоять из всех сочетаний, в которых присутствовало q_f – конечное состояние исходного автомата.

После построения ДКА из него удаляют все недостижимые состояния (состояния, переход в которые невозможен при любой входной цепочке).

В итоге построен ДКА, эквивалентный заданному НКА. При этом если исходный автомат имел n состояний, то в наихудшем случае построенный ДКА будет иметь (2ⁿ–1) состояний.

Рассмотрим на примере построение ДКА, эквивалентного заданному НКА.

1. Пусть M=({p,q,r},{0,1},d,p,{r}) – НКА, где функция переходов d задана графом:

Недетерминированный автомат M допускает все цепочки из {0,1}^, заканчивающиеся двумя единицами: (0+1)^11. Представим функцию переходов в табличном виде (таблица справа).					вход
				состояние
				p	{p}	{p,q}
				q	–	{r}
				r	–	–
	вход		Далее создадим все возможные новые состояния, которые могут получиться в результате сочетаний исходных состояний, и занесём их в таблицу. Новые состояния будем записывать в виде {pq}. Тогда из состояния p по символу 1 переход будет происходить в такое состояние pq. В таблице присутствуют недостижимые состояния q, r, pr и qr, которые можно удалить без изменения результата.
состояние
p	{p}	{pq}
q	–	{r}
r	–	–
pq	{p}	{pqr}
pr	{p}	{pq}
qr	–	{r}
pqr	{p}	{pqr}

Можно было упростить процесс и сразу заносить в новую таблицу только те состояния, которые действительно могут возникнуть. Тогда состояния pr и qr в ней бы не появились. После удаления недостижимых состояний таблица примет вид:

	вход		Для удобства переобозначим состояния: заменим p на A, pq на B, pqr – на C. Тогда начальным состоянием будет A, конечным C.		вход
состояние				состояние	0
p	{p}	{pq}		A	{A}	{B}
pq	{p}	{pqr}		B	{A}	{C}
pqr	{p}	{pqr}		C	{A}	{C}

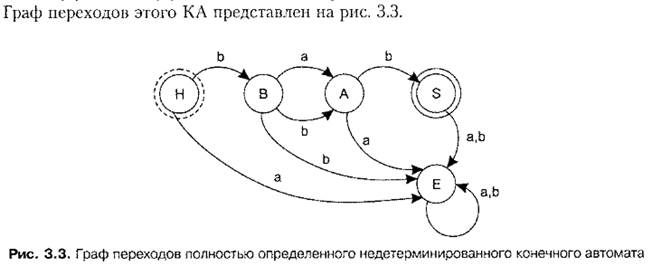
В итоге полученный детерминированный автомат, эквивалентный исходному НКА, будет иметь вид: M=({A,B,C},{0,1},d,A,{C}), граф функции переходов d:

Пусть q₁ и q₂ – состояния автомата M, на вход подается цепочка символов w длины k³0: wÎV^*, ½w½£k, (q₁,w) ├─* (q₃,l), (q₂,w) ├─* (q₄,l). Если одно из состояний (q₃ или q₄) входит в F, а другое – нет, то говорят, что цепочка w различает состояния q₁ и q₂. Если же для любой входной цепочки w длины k она не различает состояния q₁ и q₂, то говорят, что они являются k-эквивалентными или k-неразличимыми. Множество K-эквивалентных состояний составляет класс эквивалентности R(k).

Очевидно, что множества F и Q\F являются 0-эквивалентными, записывается этот факт следующим образом: R(0)={F,Q\F}.

Для построения минимального автомата строятся классы эквивалентности R(n).

Алгоритм 3.3. Построение классов эквивалентности:

1. Полагаем n:=0, строится R(0)= {F,Q\F}.

2. n:=n+1. Строится R(n) на основании R(n–1): в класс эквивалентности R(n) входят те состояния, которые по одинаковым символам переходят в n–1-эквивалентные состояния: R(n):={r_ij(n): {q_ijÎQ: "aÎV d(q_ij,a)Í r_j(n–1)} "i,jÎN}.

3. Если R(n)= R(n–1), то работа заканчивается. Иначе переход на шаг 2.

Алгоритм 3.4. Минимизация автомата:

1. Исключить все недостижимые состояния.

2. Построить классы эквивалентности.

3. Каждый из этих классов становится состоянием нового автомата.

4. Функция переходов строится на основании функции переходов исходного автомата и новых состояний.

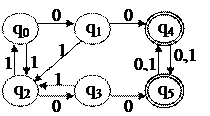Рассмотрим пример. Пусть ДКА имеет вид: M = ({q₀, q₁, q₂, q₃, q₄, q₅}, {0,1}, d, q₀, {q₄, q₅}), а функция переходов задана графом:

Требуется минимизировать данный автомат.

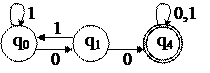Недостижимых состояний нет. Построим классы эквивалентности: R(0)={{q₀,q₁,q₂,q₃}, {q₄,q₅}}. Из состояния q₂по 0 происходит переход в q₃, а из q₁ – в q₄. Состояния q₃ и q₄находятся в разных классах эквивалентности R(0) Þ q₁ и q₂будут входить в разные классы R(1). Аналогично рассуждая про остальные состояния, получим: R(1)={{q₄,q₅},{q₀,q₂},{q₁,q₃}}. Аналогично: R(2)={{q₄,q₅}, {q₀,q₂}, {q₁,q₃}}. Þ В новом автомате 3 состояния. Обозначим их по номеру одного из состояний каждого класса. M’ = {q₀,q₁,q₄}, {0,1}, d’, q₀, {q₄}).

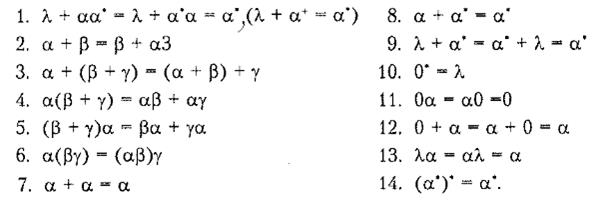
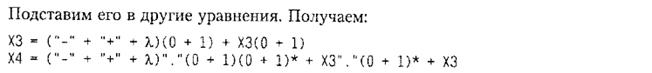
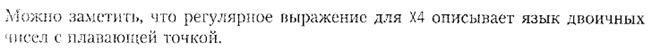
3.3.5 Расширения регулярных выражений

С тех пор как в 1950-х годах Клини (Kleene) ввел регулярные выражения с базовыми операторами для объединения, конкатенации и замыкания Клини, к ним было добавлено много расширений, повышающих их способность определять строковые шаблоны. К сожалению, в настоящее время не определены стандарты на запись расширенных регулярных выражений, и в языках программирования нотация записи шаблонов может несколько отличаться. Здесь мы рассмотрим несколько расширений в записи регулярных выражений, которые первоначально появились в утилитах Unix, таких как Lex, и которые в особенности полезны при определении лексических анализаторов.

Выражение	Соответствие	Пример
с	Один неоператорный символ с	а
\с	Символ с буквально	\*
"s"	Строка s буквально	"**"
•	Любой символ, кроме символа новой строки \n	а.*b
^	Начало строки	^{^}аbс
$	Конец строки	abc$
[s]	Любой символ из s	[abc]
[^s]	Любой символ, не входящий в s	[^{^}abc]
r*	Нуль или более строк, соответствующих r	а*
г+	Одна или более строк, соответствующих r	а+
г?	Нуль или одно r	а?
r{m,n}	От т до n повторений r	а{1,5}
r₁r₂	r₁, за которым следует r₂, конкатенация	ab
r₁\|r₂	r₁ или r₂, объединение	а\|b
(г)	То же, что и r, группировка	(a\|b)
r₁/r₂	r₁, если за ним следует r₂	abc/123

Рис. 3.8. Регулярные выражения Lex.

12 3 Следующая ⇒