ОДНОРОДНОЕ ПРЕОБРАЗОВАНИЕ КООРДИНАТ В РОБОТОТЕХНИКЕ

Уважаемые коллеги!

Электронные версии докладов на студенческую конференцию просьба высылать по адресу: eka-chudina@ya.ru. Желательно придерживаться следующей структуры статьи: введение, постановка задачи, результаты, выводы. Обязательно наличие УДК, аннотации, ключевых слов, списка литературы (образец оформления приведен ниже), данных об авторах. Объем доклада: 2-6 страниц.

Технические требования: формат страницы А4, все поля по 2 см. Шрифт Times New Roman 14, интервал полуторный. УДК статьи – выравнивание по левому краю, данные авторов – выравнивание по правому краю, название – по центру, текст статьи и список литературы – по ширине. Отступ ключевых слов, аннотации, текста статьи – 1,25 см. Выравнивание формул, таблиц и рисунков – по центру. Подпись под рисунком – выравнивание по центру. Название таблиц – перед таблицей, выравнивание по левому краю.

Образец оформления

УДК 51-7

Иванова А.М.,

студ. группы ЭАПУ-16м, ГОУ ВПО «ДонНТУ»

Руководитель: Петров И.К.,

ст. преподаватель кафедры высшей математики

им. В.В. Пака, ГОУ ВПО «ДонНТУ»

ОДНОРОДНОЕ ПРЕОБРАЗОВАНИЕ КООРДИНАТ В РОБОТОТЕХНИКЕ

Аннотация. Рассмотрено применение однородного преобразования координат при решении задач робототехники.

Ключевые слова: декартова система координат, однородное преобразование координат, робототехника.

Введение.Использование декартовой системы координат при решении задач определения положения тела в пространстве ограничивает применяемый математический аппарат, поскольку отсутствует механизм объединения операций поворота, смещения, масштабирования и перспективного преобразования.

Постановка задачи.Пусть в декартовом пространстве имеется некоторая точка M с координатами 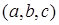. Тогда соответствующий ей вектор 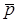можно представить в виде

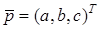. (1)

Таблица 1. Характеристика элементов, входящих в граф

Обозначение вершины	Назначение вершины
P	Наименование пласта
P₁	Вид выработок- квершлаги

Результаты.В рамках данной работы рассматривается трехмерная система координат, однородное преобразование требует нахождения матрицы T размерностью 4×4, а также взаимной ориентации ортов двух систем координат.

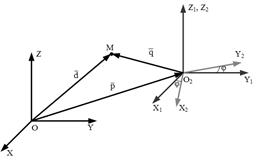
Рис. 1. Рассматриваемые системы координат

Выводы. Однородное преобразование координат находит широкое применение при реализации машинного зрения. Данный математический аппарат позволяет учесть операции переноса, масштабирования и перспективного проецирования.

Литература

1. Шафаревич И.Р. Линейная алгебра и геометрия/ И.Р. Шафаревич, А.О. Ремизов. – М.: ФИЗМАТЛИТ, 2009. – 512 с.

2. Бабич В.Н., Кремлев А.Г. Геометрическое моделирование архитектурных форм и градостроительных структур [Электронный ресурс] // «Архитектон: известия вузов», № 50, 2015. – Режим доступа: http://archvuz.ru/cont/2862 (Дата обращения: 02.04.2019).

Иванова Анна Михайловна, студентка группы ЭАПУ-16м, ГОУ ВПО «Донецкий национальный технический университет», 83001, г. Донецк, ул. Артема, 58.

Научный руководитель:

Петров Игорь Константинович, к.ф.-м.н., доцент, доцент кафедры высшей математики им. В.В. Пака, ГОУ ВПО «Донецкий национальный технический университет», 83001, г. Донецк, ул. Артема, 58.

e-mail: petrovik@mail.ru.