
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгебраическая, тригонометрическая и показательная форма комплексного числа.
1. Алгебраическая, тригонометрическая и показательная форма комплексного числа.
Алгебраическая: z = a + bi, где a – действительная часть, b – мнимая часть.
Тригонометрическая: z = r(cos ф + isin ф), r (он же |z|) – модуль комплексного числа, ф – аргумент комплексного числа.
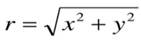
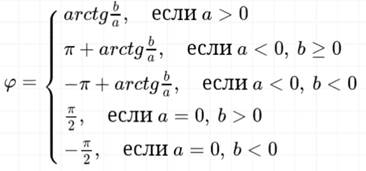
Показательная: z = 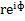 , где iф – (cos ф + isin ф).
, где iф – (cos ф + isin ф).
2. Формула Муавра. Корень n-ной степени из комплексного числа.
Формула Муавра (возвести комплексное число степень):
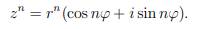
Где n – степень.
Корень n-ной степени из комплексного числа.

3. Определители, их вычисление и основные свойства.
Определителем матрицы A (определителем порядка n) называется число, равное алгебраической сумме n! произведений n слагаемых. Каждое слагаемое есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. Определитель ещё называют детерминантом. Обозначается: det A или треугольником.
Определитель 2-го порядка (матрицы 2х2) находится так:
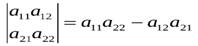
Определитель 3-го порядка (матрицы 3х3) можно найти с помощью:
а) формулой треугольников (выделенные элементы-точки перемножаются):
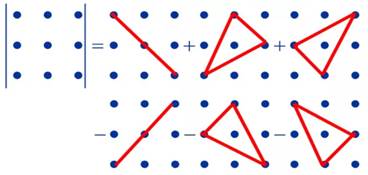
б) при помощи вычёркивания строки или столбца:



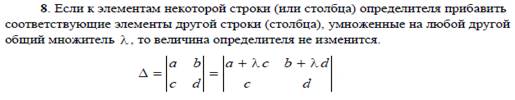
4. Формулы Крамера.
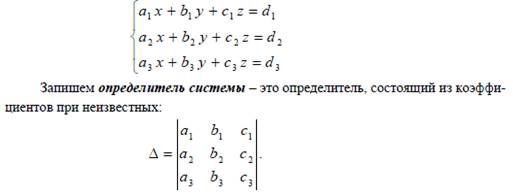

5. Обратная матрица и правила её вычисления.



6. Ранг матрицы.


|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|