Раздел 1. Основные алгоритмы сжатия текстовой информации. 1. Общие положения

Раздел 1. Основные алгоритмы сжатия текстовой информации. 1. Общие положения

Все алгоритмы, реализующие сжатие текстовой информации, относятся к классу «сжимающих без потерь» (lossless data compression). Это означает, что если у нас есть некоторый текст X_n, хранящийся в электронном виде в стандартной двоичной кодировке Unicode и имеющий объем n байт, и некоторый алгоритм компрессии 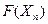, преобразующий этот текст в поток символов Y_m объема m < n, то существует обратной алгоритм 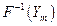, который называется алгоритмом декомпрессии, такой что .

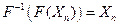К. Шеннон и Р. Фано предложили в наиболее чистом виде конструкцию кода переменной длины. В этом коде у каждого символа своя длина кодовой последовательности, как в азбуке Морзе. Но в отличие от азбуки Морзе, где конец кодовой последовательности определяется "третьим символом" — паузой, здесь нужно побеспокоиться о том, как определять завершение кода отдельного символа. Предлагается такое ограничение на код: никакая кодовая последовательность не является началом другой кодовой последовательности. Это свойство называется свойством префикса, а код, обладающий таким свойством, называется префиксным кодом.

В предположении, что кодируемые символы появляются в тексте независимо нужно стремиться уменьшать среднее число битов на один символ, т.е. математическое ожидание длины кодовой комбинации случайно выбранного символа, которое равно

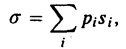
где p_i — вероятность, а s_i — длина кодовой последовательности i-го символа.

Получается экстремальная задача.

Задача о префиксном коде. Минимизировать математическое ожидание 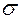по всем наборам длин { s_i }, удовлетворяющим неравенству Крафта.

Теорема Крафта: Для того, чтобы набор целых чисел 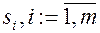, мог быть набором длин путей поиска в схеме с исходами, необходимо и достаточно, чтобы

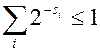Набор, для которого 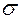минимально, называется оптимальным. Шеннон и Фано предложили строить код, близкий к оптимальному, следующим способом: разбить все символы на две группы с приблизительно равными суммарными вероятностями, коды первой группы начать с 0, а второй группы — с 1; внутри каждой группы делать то же самое, пока в каждой группе не останется только по одному символу.

Элегантный алгоритм для точного решения этой задачи предложил Д. Хаффмен. Алгоритм основывается на нескольких очевидных свойствах оптимального набора {s_j}.

Лемма 1. Пусть {р_i} — набор вероятностей символов и {s_i} — длины оптимальных кодовых комбинаций. Если p₁ > р₂ >•••> р_п, то s₁ < s₂ < ••• <s_n.

Доказательство. Здесь достаточно сослаться на уже встречавшуюся нам задачу о перестановке, минимизирующей скалярное произведение двух векторов.

Задача о минимуме скалярного произведения Пусть заданы т чисел х₁ х₂,.. , х_m и еще т чисел у₁, у₂,..., y_m. Составим пары (х, у), включив каждое х_i, и каждое у_j ровно в одну пару Затем перемножим числа каждой пары и сложим получившиеся произведения. Требуется найти такое разбиение чисел на пары, при котором значение получившейся суммы будет наименьшим.

Теорема. Наименьшее значение суммы попарных произведений достигается при сопоставлении возрастающей последовательности x, убывающей последовательности у.

Доказательство Покажем, что если найдутся две пары чисел 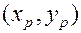и , такие что 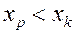и 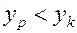, то значение суммы попарных произведений можно уменьшить, заменив эти две пары парами и Действительно, так как

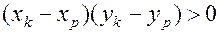, то

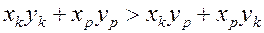Поскольку число возможных расположении равно т!, т.е. конечное число, то начиная с любого расположения за конечное число шагов мы закончим процесс улучшений на расположении, которое дальше улучшить невозможно. На нем и достигается минимум.

Лемма 2. В обозначениях и предположении леммы 1 две самые длинные кодовые комбинации имеют одинаковую длину, т.е. .

Лемма 3. Рассмотрим наравне с исходной задачей Р сокращенную задачу Р', которая получается объединением двух самых редких символов в один символ, — в предположении леммы 1 это два последних символа с суммарной вероятностью 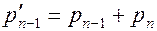. Минимальное значение целевой функции в задаче Р' отличается от значения в задаче Р на 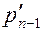, а оптимальный кодовый набор для задачи Р получается из решения для задачи Р' удлинением на один бит кодовой последовательности для объединенного символа.

Алгоритм, основанный на этих леммах, описывается в несколько строк: если в алфавите два символа, то нужно закодировать их 0 и 1, а если больше, то соединить два самых редких символа в один новый символ, решить получившуюся задачу и вновь разделить этот новый символ, приписав 0 и 1 к его кодовой последовательности.