- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 2. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Тема 2. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Интегрирование – это действие, обратное дифференцированию (нахождению производной). Для нахождения неопределённого интеграла часто достаточно воспользоваться таблицей интегралов и свойствами неопределённого интеграла. Всё это приведено ниже.
Таблица интегралов
1. 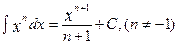 2.
2. 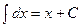 3.
3. 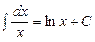 4.
4. 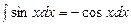 5.
5. 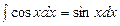 6.
6. 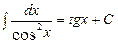
| 7. 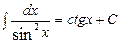 8.
8. 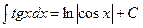 9.
9. 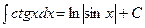 10.
10. 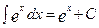 11.
11. 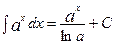 12.
12. 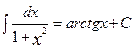
| 13. 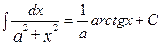 14.
14. 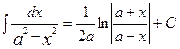 15.
15. 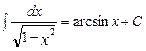 16.
16. 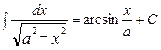
|
Свойства неопределённого интеграла.
1. 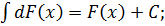
2. 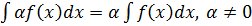 – т. е. постоянный множитель можно выносить за знак неопределённого интеграла.
– т. е. постоянный множитель можно выносить за знак неопределённого интеграла.
3. 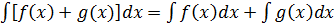 , т. е. неопределённый интеграл от суммы функций равен сумме неопределённых интегралов от этих функций.
, т. е. неопределённый интеграл от суммы функций равен сумме неопределённых интегралов от этих функций.
4. 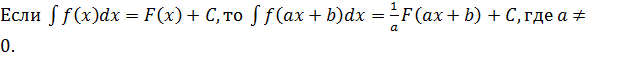
Неопределённый интеграл. Методы интегрирования
Непосредственное интегрирование
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Пример1 : Вычислите 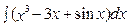
Решение: Для вычисления интеграла сначала воспользуемся 2 и 3 свойствами неопределенного интеграла, а затем применим 1 и 4 табличные интегралы:
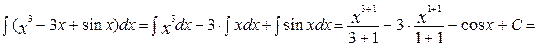
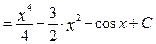
Пример2 : Вычислите 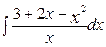
Решение: Для вычисления интеграла сначала каждый член числителя почленно разделим на знаменатель, затем воспользуемся 2 и 3 свойствами неопределенного интеграла и применим 1 и 3 табличные интегралы
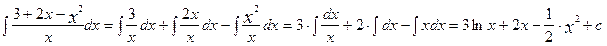
Метод замены переменной (метод подстановки)
Он является одним из наиболее эффективных и распространенных приемов интегрирования, позволяющих вомногих случаях упростить вычисление интеграла. Суть этого метода состоит в том, что путем введения новой переменной интегрирования заданный интеграл сводится к новому интегралу, который легко вычисляется непосредственным интегрированием.
Пример3 : Вычислите 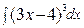
Решение: Введем новую переменную t = 3x-4, тогда 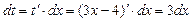 , откуда
, откуда 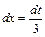 . Подставим новую переменную в интеграл
. Подставим новую переменную в интеграл
(вместо выражения 3х-4 подставим t, вместо 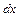 подставим
подставим 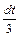 ).
).
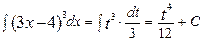
Далее нужно вернуться к первоначальной переменной. Для этого сделаем обратную замену (вместо t подставим выражение 3х-4), получим окончательный ответ.
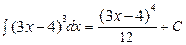
Интегрирование по частям (метод стрелок)
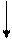
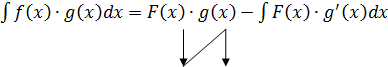
ᶴ ‘
F(x) g'(x)
«конец интегральной стрелки на начало дифференциальной минус интеграл от произведения функций на концах стрелок».
|

 Пример № 1: Найти интеграл, используя метод стрелок:
Пример № 1: Найти интеграл, используя метод стрелок: 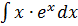 .
.Решение:
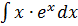 =
= 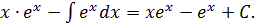
' ᶴ

Если поменять порядок стрелок, то получится более сложный интеграл. Умение выбрать нужный порядок стрелок очень важен для нахождения подобных интегралов.
Пример № 2: 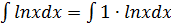 =
= 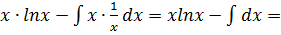
ᶴ '
x 
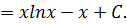
Иногда приходится применять метод стрелок несколько раз, чтобы найти нужный интеграл. Главное, чтобы каждое последующее подынтегральное выражение было проще предыдущего.


 Пример № 3:
Пример № 3: 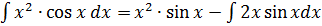 . После однократного
. После однократного
' ᶴ
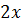
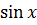
применения метода стрелок получили более простой интеграл. Тем не менее для его вычисления требуется ещё раз применить этот метод:
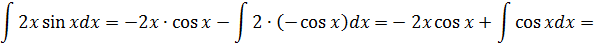
' ᶴ
2 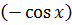
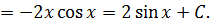
Отсюда окончательно: 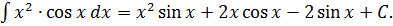
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|