Решение задач по теме «Понятие движения. Осевая и центральная симметрии»

Решение задач по теме «Понятие движения. Осевая и центральная симметрии»

Цель деятельности учителя	Создать условия для закрепления теоретических знаний по изученной теме

I этап. Актуализация опорных знаний учащихся

Сформировать уровень теоретических знаний

1. Ответьте на вопросы 7–13 (с. 297).

II этап. Решение задач

Научить применять полученные знания при решении задач

1. Разберите решение задачи № 1157.

2. Решите самостоятельную работу.

Вариант I (Б)

1. Дан четырехугольник ABСD. Постройте фигуру, симметричную данной:

а) относительно вершины D;

б) относительно диагонали АС.

2. Докажите, что при движении квадрат отображается на квадрат.

Вариант II (Х)

1. Дан четырехугольник ABСD. Постройте фигуру, симметричную данной:

а) относительно вершины А;

б) относительно диагонали BD.

2. Докажите, что при движении прямоугольник отображается на прямоугольник

№ 1157.

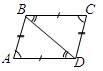
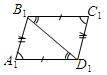Дано: ABСD и A₁B₁С₁D₁ – параллелограммы; AB = A₁B₁, AD = A₁D₁, ÐА = ÐA₁. Доказать: ABСD = A₁B₁С₁D₁. Доказательство: BС = AD,ÐА = ÐС, ÐСBD = ÐADB (накрест лежащие), то есть DABD = DBDС (по признаку). Аналогично: DA₁B₁D₁ = DВ₁С₁D₁. DABD = DA₁B₁D₁, так как AB = A₁B₁, AD = A₁D₁, ÐА = ÐA₁ (по признаку). Получаем, что DABD = DBDС = DA₁B₁D₁ = DВ₁С₁D₁. ABСD = DABD + DDBС, A₁B₁С₁D₁ = DA₁B₁D₁ + DD₁В₁С₁, значит, ABСD = A₁B₁С₁D₁

III этап. Итоги урока. Рефлексия

Домашнее задание:

решить № 1155, 1161

12 Следующая ⇒