
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема лекции: Простейшие тригонометрические уравнения.
Тема лекции: Простейшие тригонометрические уравнения.
Арксинус числа a (arcsin а) - такой угол а из промежутка 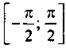 , синус которого равен а, т. е.
, синус которого равен а, т. е. 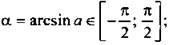
Арккосинус числа a (arccos а) - такой угол а из промежутка [0; π], косинус которого равен а, т. е. 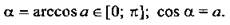
Арктангенс числа a (arctg а) - такой угол а из промежутка 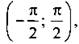 тангенс которого равен а, т. е.
тангенс которого равен а, т. е. 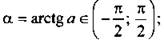 tg а = а.
tg а = а.
Арккотангенс числа a (arcctg а) - такой угол а из промежутка (0; π), котангенс которого равен а, т. е. 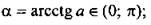 ctg а = а.
ctg а = а.
| Уравнение | Решение |
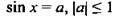
| 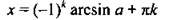
|
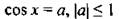
| 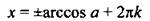
|
| tgx = а | 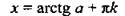
|
| ctg х = а | 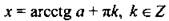
|
Пример 1 Решим уравнение 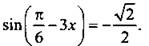
Так как функция синус нечетная, то запишем уравнение в виде 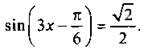 Решения этого уравнения:
Решения этого уравнения: 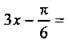
 откуда находим
откуда находим 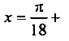
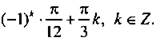
Пример 2 Решим уравнение 
По приведенной формуле запишем решения уравнения: 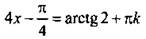 и найдем
и найдем 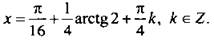
Заметим, что в частных случаях (а = 0; ±1) при решении уравнений sin х = а и cos х = а проще и удобнее использовать не общие формулы, а записывать решения на основании единичной окружности:
для уравнения sin х = 1 решения 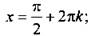
для уравнения sin х = 0 решения х = πk;
для уравнения sin х = -1 решения 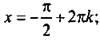
для уравнения cos х = 1 решения х = 2πk;
для уравнения cos х = 0решения 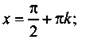
для уравнения cos х = -1 решения 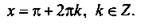
Пример 3 Решим уравнение 
Так как в данном примере имеется частный случай уравнения, то по соответствующей формуле запишем решение: 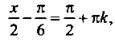 откуда найдем
откуда найдем 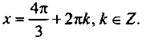
1.Решить уравнение:
а) 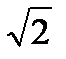 sin x -1 = 0;
sin x -1 = 0;
б) tg 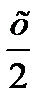 -
- 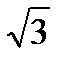 = 0;
= 0;
Пример 4 Найдем решения уравнения  принадлежащие отрезку [0; π].
принадлежащие отрезку [0; π].
Решим данное уравнение, используя числовую окружность. Получим: 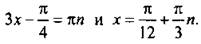 Отберем те решения, которые принадлежат отрезку [0; π]. По условию получим неравенство
Отберем те решения, которые принадлежат отрезку [0; π]. По условию получим неравенство  Решим это неравенство:
Решим это неравенство: 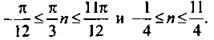 В этот промежуток попадают три целых значенияn: n = 0, 1, 2. Для этих значении n найдем соответствующие решения:
В этот промежуток попадают три целых значенияn: n = 0, 1, 2. Для этих значении n найдем соответствующие решения: 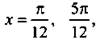
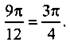
Пример 5 Решим уравнение 
Используя общую формулу, получим: 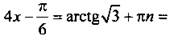
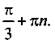 Тогда
Тогда 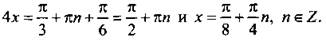
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|