Хелпикс

Главная

Контакты

Случайная статья



Применение производной к исследованию функций



Применение производной к исследованию функций

1.

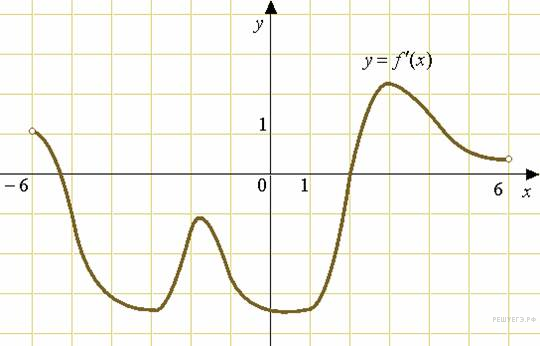
На ри­сун­ке изображен график производной функ­ции 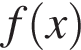, опре­де­лен­ной на ин­тер­ва­ле 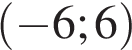. Най­ди­те промежутки воз­рас­та­ния функции 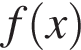. В от­ве­те укажите сумму целых точек, вхо­дя­щих в эти промежутки.

2.

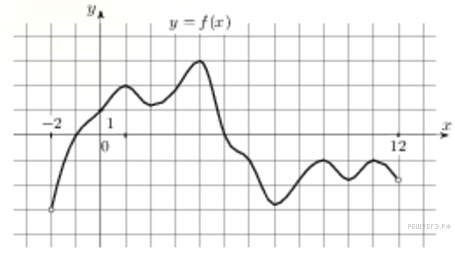На ри­сун­ке изоб­ра­жен гра­фик функ­ции y = f(x), опре­де­лен­ной на ин­тер­ва­ле (−2; 12). Най­ди­те сумму точек экс­тре­му­ма функ­ции y = f(x).

3.

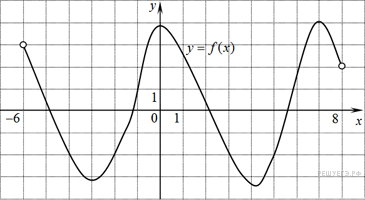
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.

4.

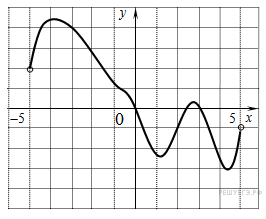На рисунке изображен график функции 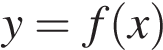, определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции 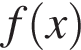отрицательна.

5.

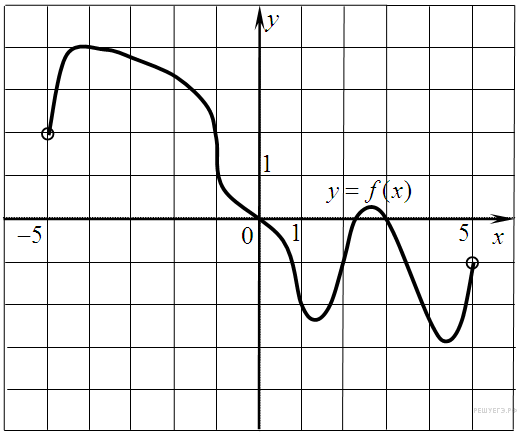На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.

6.

На ри­сун­ке изображен гра­фик функции y = f(x), опре­де­лен­ной на ин­тер­ва­ле (−2; 12). Най­ди­те сумму точек экс­тре­му­ма функции f(x).

7.

На рисунке изображён график y=f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2 ] функция f(x) принимает наибольшее значение?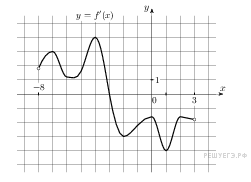

8.

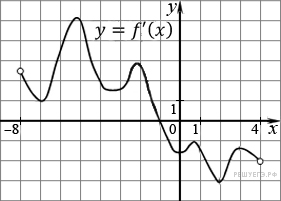На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?

 

 

9.

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

 

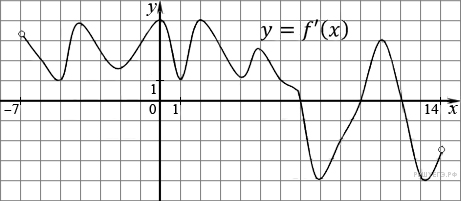
10.

На рисунке изображен график производной функции f(x), определенной на интервале (−18; 6). Найдите количество точек минимума функции f(x) на отрезке [−13;1].

 

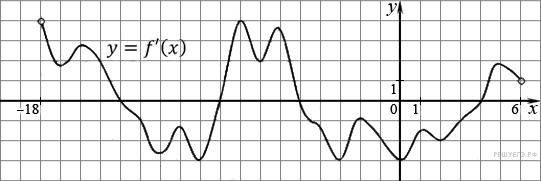
11.

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

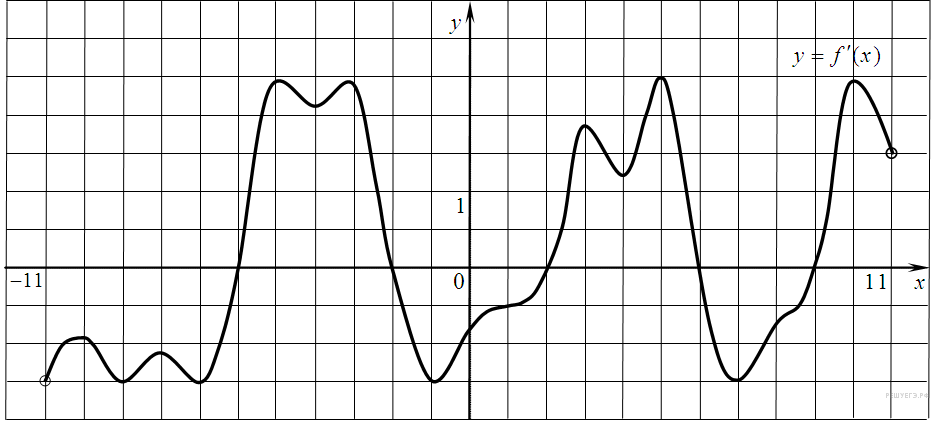
12.

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

 

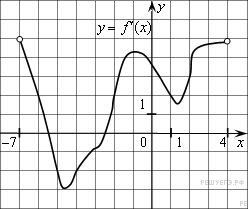
13.

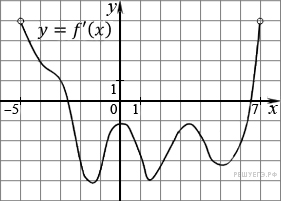На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

 

14.

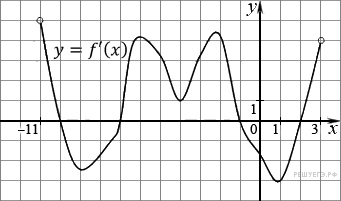
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

 

15.

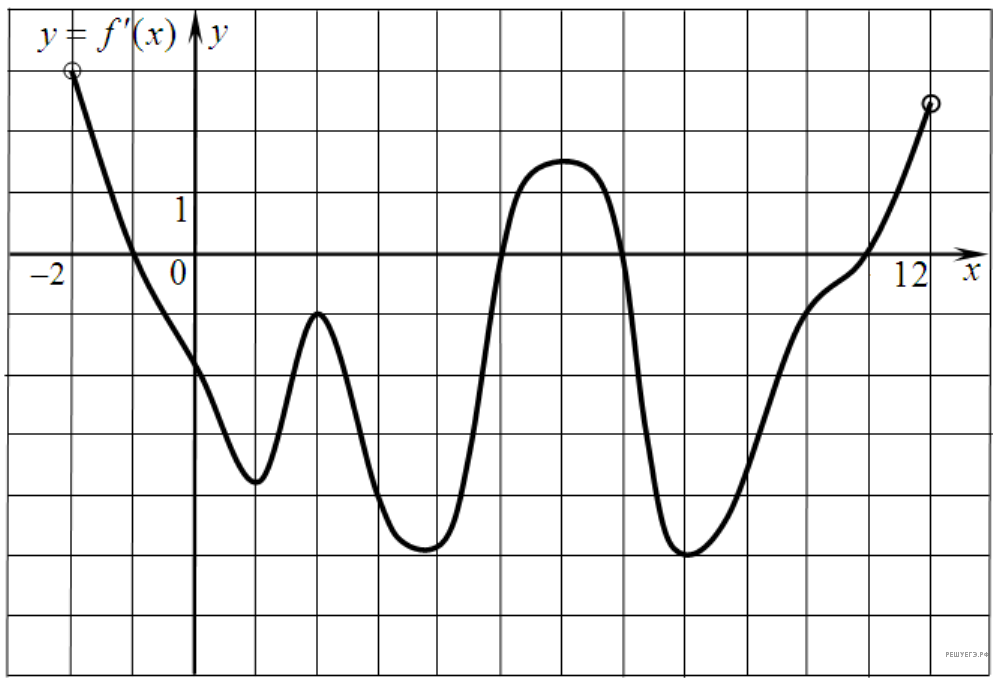
На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

16.

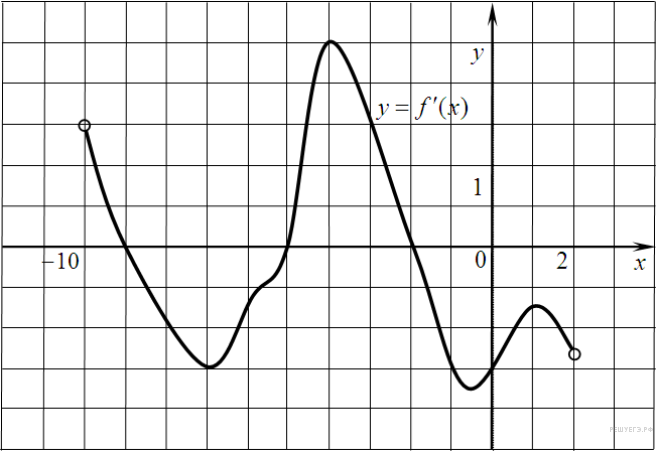
На ри­сун­ке изображен гра­фик производной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−10; 2). Най­ди­те количество точек, в ко­то­рых касательная к гра­фи­ку функции f(x) па­рал­лель­на прямой y = −2x − 11 или сов­па­да­ет с ней.

 

17.

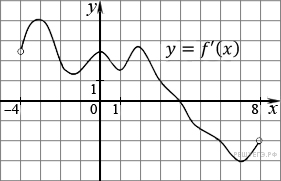На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].

18.

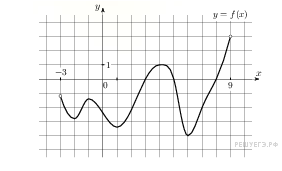На рисунке изображен график функции y=f(x) , определенной на интервале (−3; 9) . Найдите количество точек, в которых производная функции f(x)равна 0.

19.

На ри­сун­ке изображён гра­фик 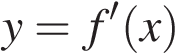- про­из­вод­ной функции f(x).На оси абсцисс отмечены во­семь точек: x1, x2, x3, ..., x8. Сколько из этих точек лежит на промежутках возрастания функции f(x) ?

 

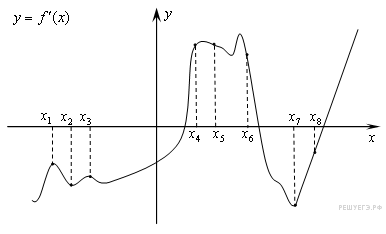
20.

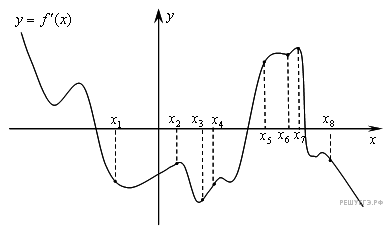
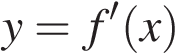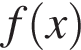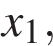
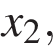
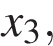
На ри­сун­ке изображён гра­фик про­из­вод­ной функции и во­семь точек на оси абсцисс: , 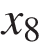. В сколь­ких из этих точек функ­ция 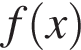убывает?

 

21.

На ри­сун­ке изображен гра­фик функции 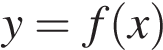и от­ме­че­ны точки −2, −1, 1, 4. В какой из этих точек зна­че­ние производной наименьшее? В от­ве­те укажите эту точку.

 

22.

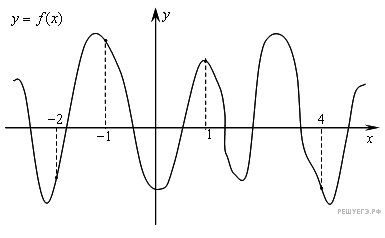
На ри­сун­ке изображён гра­фик функции у = f'(x) — про­из­вод­ной функции f(x) определённой на ин­тер­ва­ле (1; 10). Най­ди­те точку ми­ни­му­ма функции f(x).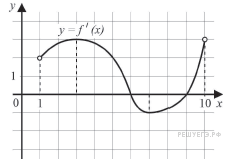

23.

Функция y = f (x) опре­де­ле­на и не­пре­рыв­на на от­рез­ке [−5; 5]. На ри­сун­ке изображён гра­фик её производной. Най­ди­те точку x0, в ко­то­рой функ­ция при­ни­ма­ет наи­мень­шее значение, если f (−5) ≥ f (5).

24.

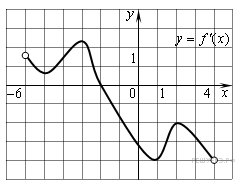Функция 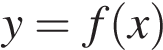опре­де­ле­на на про­ме­жут­ке 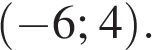На ри­сун­ке изоб­ра­жен гра­фик ее производной. Най­ди­те абс­цис­су точки, в ко­то­рой функ­ция 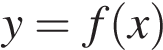при­ни­ма­ет наи­боль­шее значение.

25.

На ри­сун­ке изоб­ра­жен гра­фик функ­ции y = f(x), опре­де­лен­ной на ин­тер­ва­ле (−3; 9). Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на пря­мой y = 12 или сов­па­да­ет с ней.

 

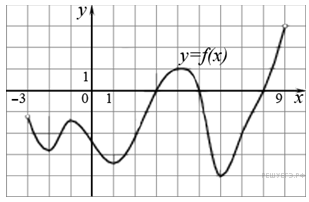
26.

На ри­сун­ке изоб­ра­жен гра­фик функ­ции y = f(x), опре­де­лен­ной на ин­тер­ва­ле (−6; 5). Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на пря­мой y = −6.

 

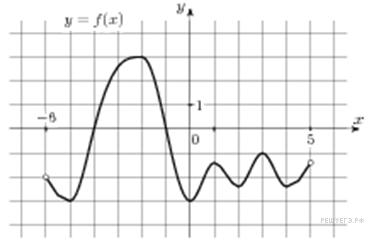
27.

Ма­те­ри­аль­ная точка дви­жет­ся от на­чаль­но­го до ко­неч­но­го положения. На ри­сун­ке изображён гра­фик её движения. На оси абс­цисс от­кла­ды­ва­ет­ся время в секундах, на оси ор­ди­нат — рас­сто­я­ние от на­чаль­но­го по­ло­же­ния точки (в метрах). Най­ди­те сред­нюю ско­рость дви­же­ния точки. Ответ дайте в мет­рах в секунду.

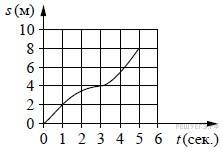
28.

Ма­те­ри­аль­ная точка дви­жет­ся от на­чаль­но­го до ко­неч­но­го положения. На ри­сун­ке изображён гра­фик её движения. На оси абс­цисс от­кла­ды­ва­ет­ся время в секундах, на оси ор­ди­нат — рас­сто­я­ние от на­чаль­но­го по­ло­же­ния точки (в метрах). Най­ди­те сред­нюю ско­рость дви­же­ния точки. Ответ дайте в мет­рах в секунду.

 
  

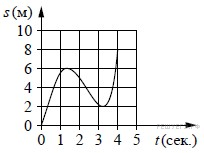
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.