
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
План-конспект урока «Применение производной к исследованию функций и построению графика функции»
План-конспект урока «Применение производной к исследованию функций и построению графика функции»
1. Образовательные цели:
-Научить применять производную к исследованию функции
- Научить строить график функции на основе проведённого исследования.
- систематизировать и совершенствовать знания, умения и навыки учащихся при решении задач;
2. Развивающие цели:
- формирование активного, самостоятельного творческого мышления;
- наблюдательности, сообразительности, инициативы;
- умения анализировать, сравнивать и обобщать;
- учить проводить рассуждения, используя математическую речь;
3. Воспитательные цели:
- формирование нравственных качеств личности: аккуратности, дисциплинированности, трудолюбия, ответственности, креативности, требовательности к себе, любознательности.
Оборудование: компьютер, презентация, интерактивная доска, программа 
Ход урока:
I этап: Организационный
II этап: Подготовительный
Устная работа
1. Найдите производную функции: (Слайд 1, 2):
а) sin x
б) tg х
в) х2 + 2
г) х4
д) 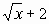
е) ех+2
2. Найдите промежутки возрастания и убывания функции, точки экстремума (Слайд 3):
III этап: Решение задач
Тема нашего занятия – «Исследование функции и построение графиков с помощью производной».
Цель урока – научиться строить график функции, применяя производную для исследования функции.
-Одним из важнейших этапов построения графика функции является определение экстремумов функции и как вы знаете это удобно делать с помощью производной.
Задание1: исследовать на наличие экстремумов функцию f(x)= 
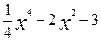 и построить эскиз её графика.
и построить эскиз её графика.
1. 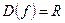 .
.
2. 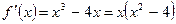
3. 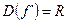
4. 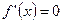 при х=0, х=2, х=-2
при х=0, х=2, х=-2
5. Точки пересечения с осями координат (-3;0), (3;0)
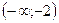
| –2 | 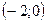
| 
| 
| |||
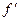
| _ | + | _ | + | |||
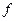
| æ | -7 | ä | -3 | æ | -7 | ä |
| min | max | min |
Наносим полученные точки на координатную плоскость. Возникает проблема: какой линией соединить имеющиеся точки графика, чтобы она более точно передавала свойства заданной функции? Предлагаем 4 варианта соединения точек. Какой из них верный? (Слайд 4)
1 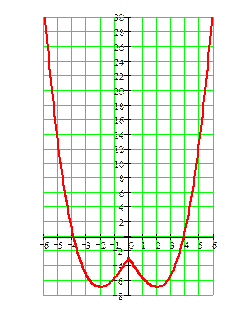
| 2 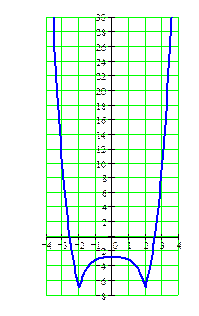
|
3 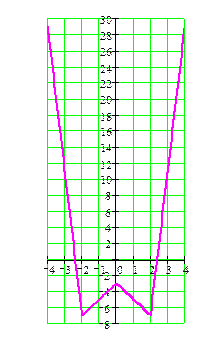
| 4 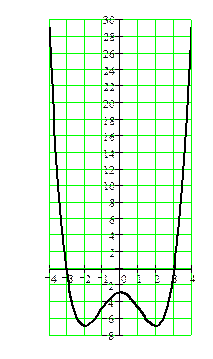
|
· Ответить на вопрос, можно вспомнив, что во всех найденных точках экстремумов производная равна нулю. Значит, касательные к графику функции в этих точках должны быть параллельны оси ОХ. Это возможно только на рисунке 4. Таким образом, линия представленная на рисунке 4 наиболее точно отражает свойства заданной функции. Вывод: при построении графика при помощи исследования функции с помощью производной нужно использовать не только координаты точек экстремума, но и всю аналитически найденную информацию.
- Задание2. Глядя на данную таблицу, постройте схематично график функции (слайд 5).
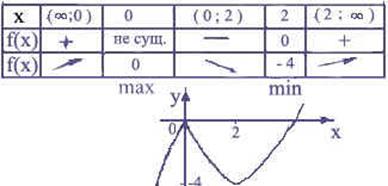
Задание3. По графику самостоятельно заполнить таблицу (слайд 6)
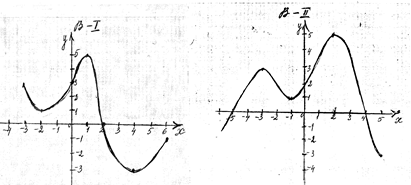
Задание4. Построить графики функций на компьютере и определить по графику их точки экстремума
( слайд 7)
а) 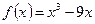 ;
;
б) 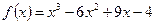
При определении точек экстремума возникла проблема: для функции б) найти точки экстремума с помощью построения графика на компьютере можно точно, а для функции а) – лишь приближённо. а) 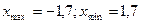 ;
;
б) 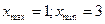
Разрешить проблему можно, применяя аналитический метод. Найдем точки экстремума предложенных функций, используя производную (учащиеся приводят аналитическое решение проблемы)
а) 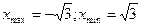 ;
;
б) 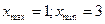
Вывод: аналитический способ нахождения точек экстремума более совершенный по сравнению с графическим.
IV этап: Итог урока.
Какие выводы мы сделали сегодня на уроке:
· для уточнения графика, важно использовать все этапы исследования функции
· аналитический способ нахождения точек экстремума более совершенный по сравнению с графическим
· при построении графика при помощи исследования функции с помощью производной нужно использовать всю аналитически найденную информацию
Проведём блиц-тест (на компьютере)
VI этап: Домашнее задание.
Исследуйте функции, на основе проведённого исследования постройте графики этой функции в тетради, а на следующем занятии проверьте построение графика с помощью компьютера.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|