
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение предела функции. Теорема о единственности предела. Основные теоремы о пределах функций. Теорема №1.. Теорема №2.. Теорема №3.. Бесконечно малые и бесконечно большие функции. Определение№1.. Определение№2.
Определение предела функции
Пределом функции 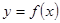 при
при 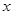 стремящемся к
стремящемся к 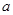 называется число
называется число 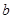 , к которому стремится значение самой функции при
, к которому стремится значение самой функции при 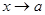 и обозначается
и обозначается 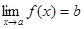 .
.
Теорема о единственности предела
Если функция 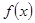 имеет при
имеет при 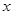 , стремящемся к
, стремящемся к 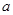 , то этот предел единственный.
, то этот предел единственный.
Основные теоремы о пределах функций
Теорема №1.
Если существуют пределы функции 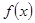 и
и 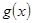 при
при 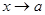 , то существует так же и предел их суммы, равный сумме пределов функций
, то существует так же и предел их суммы, равный сумме пределов функций 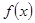 и
и 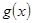 при
при 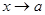 :
:
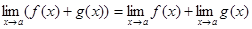 .
.
Теорема №2.
Если существуют пределы функции 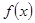 и
и 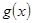 при
при 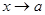 , то существует так же и предел их произведения, равный произведению пределов функций
, то существует так же и предел их произведения, равный произведению пределов функций 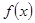 и
и 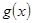 при
при 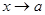 :
:
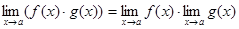 .
.
Теорема №3.
Если существуют пределы функции 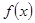 и
и 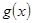 при
при 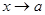 и предел функции
и предел функции 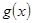 отличен от нуля, то существует так же и предел отношения (дроби), равный отношению пределов функций
отличен от нуля, то существует так же и предел отношения (дроби), равный отношению пределов функций 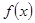 и
и 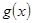 при
при 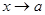 :
:
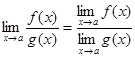 , если
, если 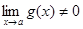 .
.
Следствия:
1. Постоянный множитель можно вынести за знак предела: 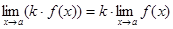 .
.
2. 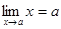 .
.
3. 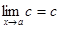 .
.
4. Если n- натуральное число, то 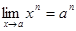 ,
, 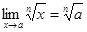 .
.
Бесконечно малые и бесконечно большие функции
Определение№1.
Функция 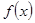 называется бесконечно малой при
называется бесконечно малой при 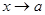 , если
, если 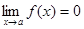 .
.
Определение№2.
Функция 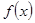 называется бесконечно большой при
называется бесконечно большой при 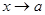 , если
, если 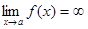 или
или 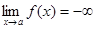 .
.
Отметим свойства бесконечно малых и бесконечно больших функций.
1. Если функции 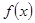 и
и 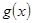 - бесконечно малые при
- бесконечно малые при 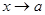 , то их сумма
, то их сумма 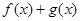 при
при 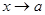 также является бесконечно малой.
также является бесконечно малой.
2. Если функция 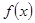 - бесконечно малая при
- бесконечно малая при 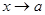 , а
, а 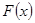 - ограниченная функция, то их произведение
- ограниченная функция, то их произведение 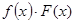 , есть бесконечно малая величина.
, есть бесконечно малая величина.
Следствие.Произведение конечного числа бесконечно малых функций есть величина бесконечно малая.
3. Если функция 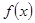 при
при 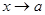 имеет конечный предел
имеет конечный предел 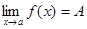 , функция
, функция 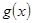 - бесконечно большая, то
- бесконечно большая, то 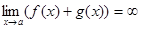 ;
; 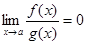 .
.
4. Если функция 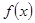 - бесконечно малая при
- бесконечно малая при 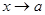 , то функция
, то функция 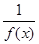 - бесконечно большая, т.е.
- бесконечно большая, т.е. 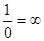 .
.
5. Если функция 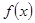 - бесконечно большая при
- бесконечно большая при 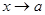 , то функция
, то функция 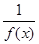 - бесконечно малая, т.е.
- бесконечно малая, т.е. 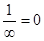 .
.
Выражения вида 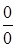 ,
, 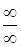 ,
, 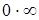 ,
, 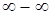 ,
, 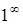 ,
, 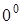 ,
, 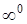 называются неопределенностями.
называются неопределенностями.
Вычисление предела функции в этих случаях называют раскрытием неопределенности.
Неопределенность вида 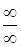
Правило.Чтобы раскрыть неопределенность вида 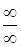 , заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
, заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
Например, 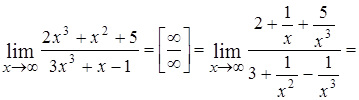
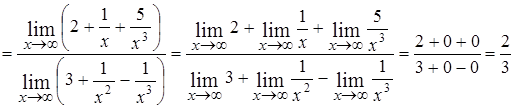 .
.
Неопределенность вида 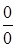
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|