Практическая работа №17.. Тема: Расстояние между точками

Практическая работа №17.

Тема: Расстояние между точками

Цель урока: вывод формулы для нахождения расстояния между двумя точками, заданными координатами, и применение формул к решению задач.

Методические материалы

Пусть А(х1; у1), В(х2; у2). Найдем расстояние между точками А и В.

Рассмотрим сначала случай х1 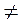х2, y1 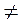y2

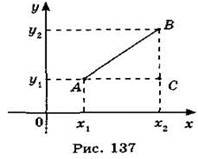
Проведем AC 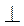BC. В прямоугольном треугольнике ABC имеем:

АС = |х2 - х1|, ВС = |у2 - у1|. По теореме Пифагора имеем: АВ2 = АС2 + ВС2 или АВ = ,

АВ = 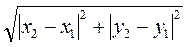= 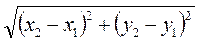. (1)

Если у1 = у2 и х1 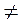х2, то АВ = |х2 - х1|. Такой же результат в этом случае дает и формула (1).

Если х1 = х2 и у1 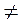у2, то АВ = |y2 - y1|. Такой результат дает и формула (1).

Наконец, х1 = х2, у1 = у2, то есть если точки А и В совпадают, формула (1) дает нужный результат: АВ = 0.

Итак, как бы не были размещены на координатной плоскости точки А(х1; у1), В(х2; у2), всегда имеем: АВ = .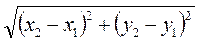

Решение задач

1. Найдите АВ, если А(-1; 3), В(3; 0). (Ответ. АВ = 5)

2. Найдите расстояние от точки А(-5; 12) до начала координат. (Ответ.ОА = 13)

3. Найдите периметр треугольника ABC, если А(-1; 2), В(3; -1), С(-1; -1). (Ответ. 12)

4. Лежат ли на одной прямой точки А, В, С, если:

а) А(1; 4), В(4; 0), С(2; 2);

б) А(1; 4), В(4; 0), С(2,5; 2)?

(Ответ а) Нет; б) да)

5. Какая из точек А (2; 4) В(-3; 2) - лежит ближе к началу координат? (Ответ. В)

6. Даны точки А (-2; 5), В (1; 8). Найдите точку, равноудаленную от точек А и В, которая лежит:

а) на оси Ох;

б) оси Оу;

в) отрезка АВ.

(Ответ а) (6; 0); б) (0; 6); в) (-0,5; 6,5).)

7. Найдите радиус круга, центром которого является точка М(-4; 3), а точка А(-4; 2) лежит на окружности.