Билет №1.. Свойство медиан треугольника. Свойство отрезков касательных, проведенных к окружности из одной точки.. Признаки подобия треугольников.. Признак параллелограмма (по точке пересечения диагоналей).. Свойства противоположных сторон и углов парал

Билет №1.

Фигура, составленная из отрезков АВ, ВС, СD, ..., ЕF, FА так, что смежные отрезки (т. е. отрезки АВ и ВС, ВС и СD, ..., FА и АВ) не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Такая фигура называется многоугольником (рис. 150).

Точки А, В, С, ..., Е, F называются вершинами, а отрезки АВ, ВС, СD, ..., ЕF, FА — сторонами многоугольника.

Сумма длин всех сторон называется периметром многоугольника.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

Билет №2.

Свойство медиан треугольника

Билет №3.

Билет №4.

ромбе

ромба

Билет №5.

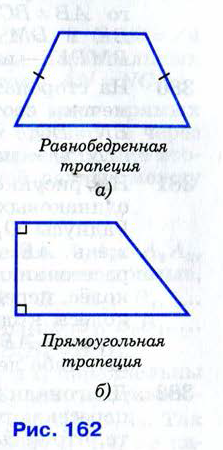
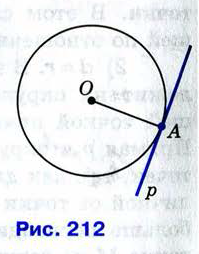
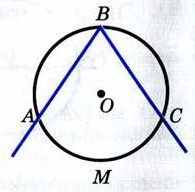
Свойство отрезков касательных, проведенных к окружности из одной точки.

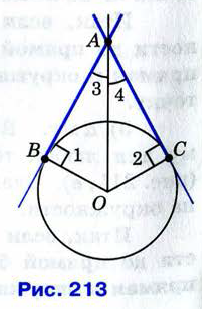
Билет №6.

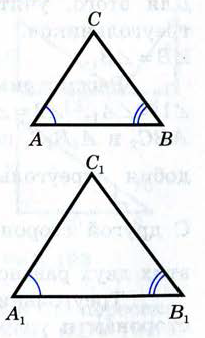
Признаки подобия треугольников.

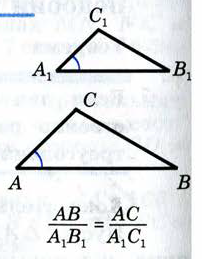
Признак параллелограмма (по точке пересечения диагоналей).

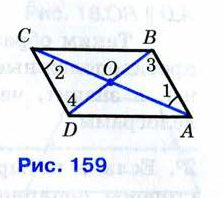
Билет №7.

Свойство диагоналей параллелограмма

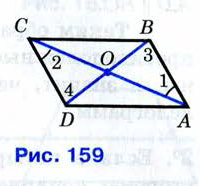
Билет №8.

Свойства противоположных сторон и углов параллелограмма.

Если

Билет №9.

Свойство диагоналей прямоугольника.

Билет №10.

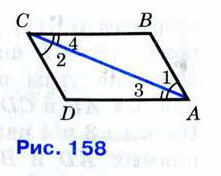
Признак параллелограмма по двум противоположным сторонам, которые равны и параллельны.

Билет №11.

Билет №12.

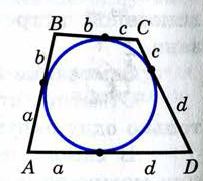
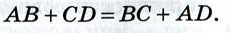
Свойство диагоналей ромба.

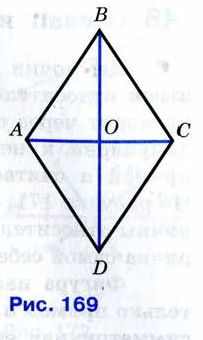
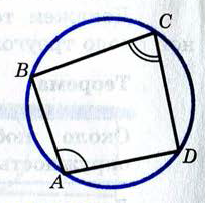Билет №13.

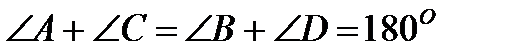
Билет №14.

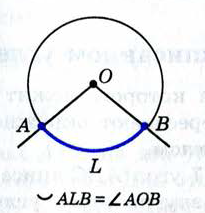
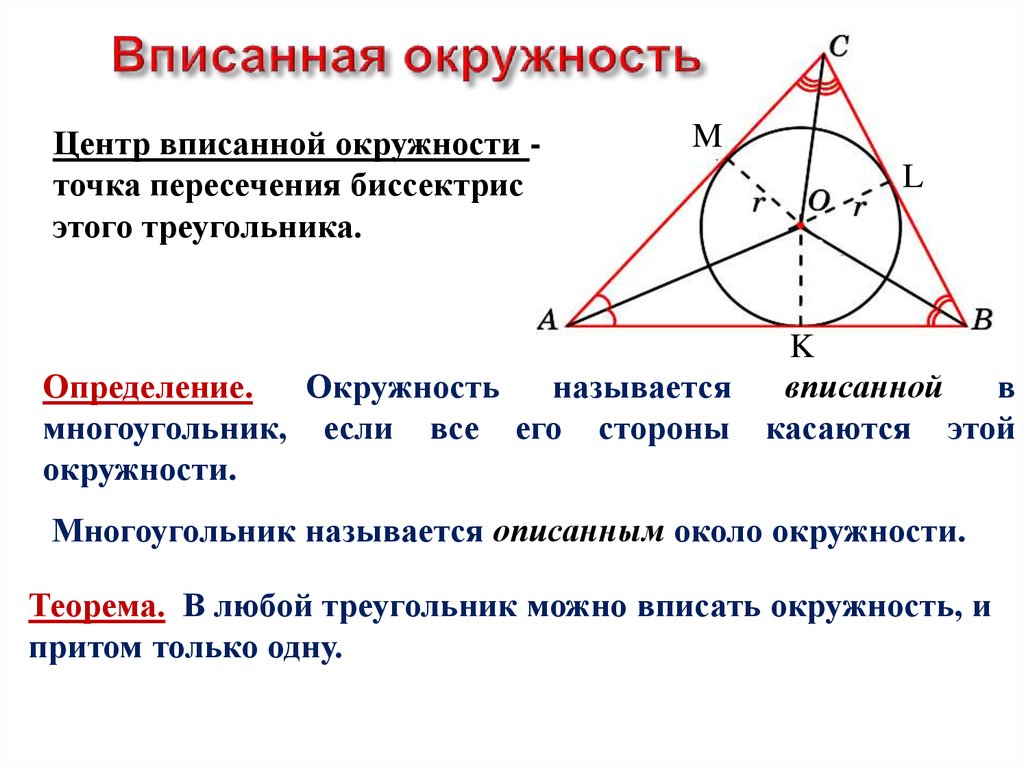
Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник – описаннымоколо этой окружности.

Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник – вписаннымв эту окружность.

12 Следующая ⇒