
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Правила дифференцирования
Тема: Основные понятия линейной алгебры и математического анализа
План занятия:
1. Матрицы. Произведение матриц. Обратная матрица
2. Системы линейных алгебраических уравнений. Формулы Крамера
3. Понятие предела функции.
4. Понятие производной функции. Правила дифференцирования.
Вопрос 1. Матрицы. Произведение матриц. Обратная матрица
Матрицы в математике - один из важнейших объектов, имеющих прикладное значение.
Прямоугольная таблица, состоящая из чисел, расположенных в m строках и n столбцах, называетсяmn-матрицей(или просто матрицей) и записывается так:
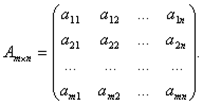 (1)
(1)
В матрице (1) числа 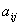 называются её элементами (как и в определителе, первый индекс означает номер строки, второй – столбца, на пересечении которых стоит элемент; i = 1, 2, ..., m; j = 1, 2, n).
называются её элементами (как и в определителе, первый индекс означает номер строки, второй – столбца, на пересечении которых стоит элемент; i = 1, 2, ..., m; j = 1, 2, n).
Матрица называется прямоугольной, если 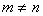 .
.
Если же m = n , то матрица называется квадратной, а число n – её порядком.
Определителем квадратной матрицы A называется определитель, элементами которого являются элементы матрицы A . Он обозначается символом |A|.
Квадратная матрица называется неособенной (невырожденной), если её определитель не равен нулю, и особенной (вырожденной), если её определитель равен нулю.
Матрицы называются равными, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают.
Матрица называется нулевой, если всё её элементы равны нулю. Нулевую матрицу будем обозначать символом 0 или 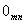 .
.
Матрица A', которая получается из матрицы A заменой в ней местами строк и столбцов, называется транспонированной относительно матрицы A. Таким образом, для матрицы (1) транспонированной является матрица

Главной диагональю квадратной матрицы называется воображаемая линия, соединяющая её элементы, у которых оба индекса одинаковые. Эти элементы называются диагональными.
Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной. Не обязательно все диагональные элементы диагональной матрицы отличны от нуля. Среди них могут быть и равные нулю.
Квадратная матрица, у которой элементы, стоящие на главной диагонали равны одному и тому же числу, отличному от нуля, а все прочие равны нулю, называется скалярной матрицей.
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице. Например, единичной матрицей третьего порядка является матрица
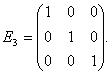

Определение.Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.
Из этого определения следует формула элемента матрицы C:
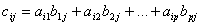
Произведение матрицы А на матрицу В обозначается АВ.
Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица 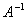 , произведение на которую матрицы А справа является единичной матрицей, т.е,
, произведение на которую матрицы А справа является единичной матрицей, т.е, 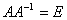 .
.
Пример 1. Даны две матрицы А и В. Найти: а) АВ; б) ВА; в) 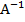 .
.



Вопрос 2. Системы линейных алгебраических уравнений. Формулы Крамера
Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
В общем виде система m линейных уравнений с n переменными записывается так:
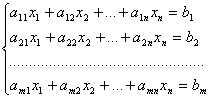 . (2)
. (2)
Числа 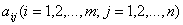 называются коэффициентами при переменных, а
называются коэффициентами при переменных, а 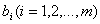 -
-
свободными членами.
Совокупность чисел 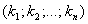 называется решением системы (2) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.
называется решением системы (2) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается  (дельта).
(дельта).
Определители ∆x1, ∆x2 получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
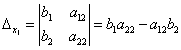
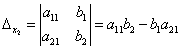
Формулы Крамера для нахождения неизвестных: 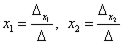 .
.
Найти значения x1 и x2 возможно только при условии, если 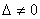 .
.
Пример 2. Решить систему уравнений по формулам Крамера.
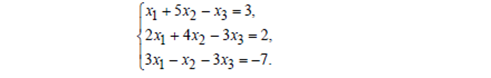

Вопрос 3. Понятие предела функции.
Определение 1. Число A называется пределом функции f(x) в точке 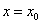 (или при
(или при 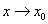 ), если для любой сходящейся к
), если для любой сходящейся к 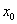 последовательности значений аргумента x, отличных от
последовательности значений аргумента x, отличных от 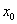 , соответствующая последовательность сходится к числу A.
, соответствующая последовательность сходится к числу A.
Символически это записывается так:
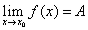
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.
Основные неопределённости пределов:

Для того чтобы устранить неопределённость, необходимо использовать некоторые правила и методы решения пределов. Рассмотрим их на конкретных примерах.
Пример 1. Найти предел заданной функции:
а) 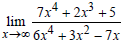 б)
б) 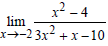 в)
в) 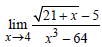
г) 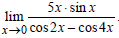 д)
д) 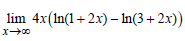





Вопрос 4. Понятие производной функции. Правила дифференцирования.
Производной функции у=ƒ(х) β точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Итак, по определению
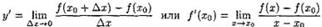
Производная функции ƒ(х) есть некоторая функция f'(x), произведённая из данной функции.
Функция у=ƒ(х), имеющая производную в каждой точке интервала (a;b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
Значение производной функции у=ƒ(х) в точке х=х0 обозначается одним из символов: ƒ'(х0), у'|x=xo или у'(х0).
Правила дифференцирования
Правило 1. Постоянный множитель c можно выносить за знак производной:
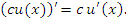
Правило 1 непосредственно вытекает из определения производной функции и свойства пределов функций, согласно которому постоянный множитель можно выносить за знак предела.
Правило 2. Если существуют производные 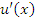 и
и 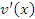 , то производная от суммы (разности) функций
, то производная от суммы (разности) функций  и
и 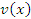 равна сумме (разности) производных:
равна сумме (разности) производных:
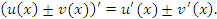
Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.
Правило 3. 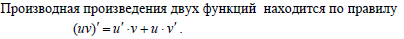
Правило 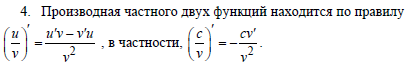
Формулы вычисления производных функций:
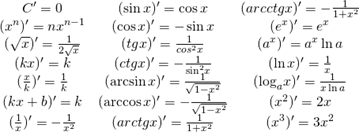
Пример 2.Вычислить производную функции: 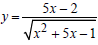
Решение:
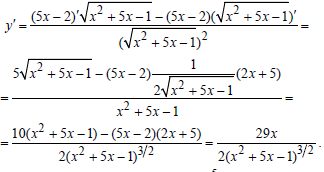
Пример 3.Вычислить производную функции: 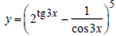
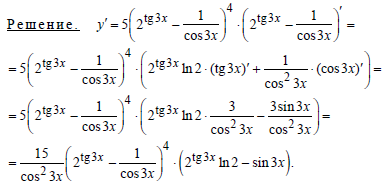
Пример 4.Вычислить производную функции: 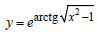
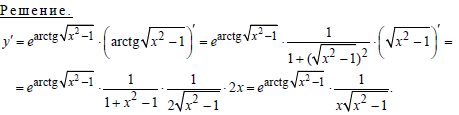
Пример 5.Вычислить производную функции: 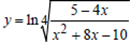
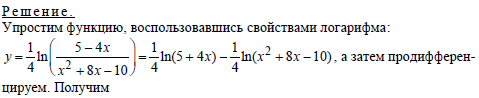
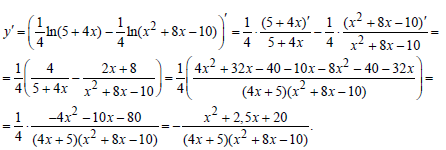
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|