
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производная сложной функции.
Определение производной. Ее физический и геометрический смысл.
Правила и формулы вычисления производной.
1. Определение производной.
Понятие производной является одним из основных математических понятий и одной из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.
Самое главное — понять смысл. Запомним определение: производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
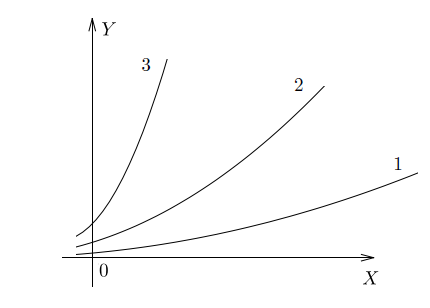 Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем? На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается одним из символов:
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем? На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается одним из символов: 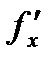 , , 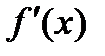 , , 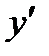 , , 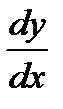 , , 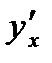 .
Функция, имеющая производную, называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
2. Физический и геометрический смысл производной.
Можно сказать, что если функция описывает какой-либо физический процесс, то производная .
Функция, имеющая производную, называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
2. Физический и геометрический смысл производной.
Можно сказать, что если функция описывает какой-либо физический процесс, то производная 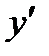 есть скорость протекания этого процесса. Пусть есть скорость протекания этого процесса. Пусть 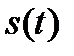 - зависимость пути от времени, тогда - зависимость пути от времени, тогда 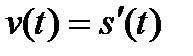 . Скорость – производная пути по времени. Ускорение – производная скорости по времени, т.е. . Скорость – производная пути по времени. Ускорение – производная скорости по времени, т.е. 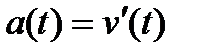 . В этом состоит физический смысл производной.
Покажем, как найти . В этом состоит физический смысл производной.
Покажем, как найти 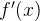 с помощью графика. с помощью графика.
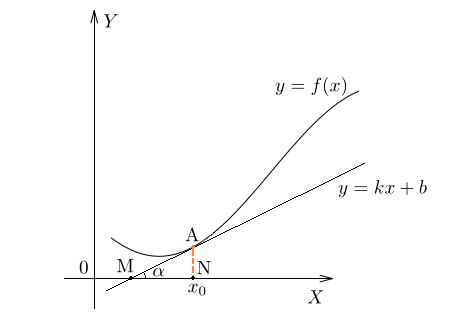 Нарисован график некоторой функции
Нарисован график некоторой функции 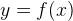 . Возьмем на нем точку . Возьмем на нем точку 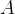 с абсциссой с абсциссой 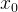 . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.
Производная функции . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.
Производная функции 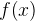 в точке в точке 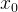 равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке. равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
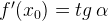 .
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси 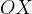 .
Что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Мы получаем, что .
Что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Мы получаем, что 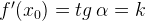 .
Запомним эту формулу. Она выражает геометрический смысл производной. Производная функции в точке .
Запомним эту формулу. Она выражает геометрический смысл производной. Производная функции в точке 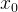 равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Другими словами, производная равна тангенсу угла наклона касательной.
Уравнение касательной равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Другими словами, производная равна тангенсу угла наклона касательной.
Уравнение касательной 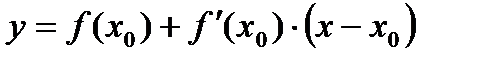 .
3. Правила и формулы вычисления производной функции.
Нахождение производной функции связано с определенными трудностями. На практике функции дифференцируются с помощью ряда правил и формул.
Правила дифференцирования: .
3. Правила и формулы вычисления производной функции.
Нахождение производной функции связано с определенными трудностями. На практике функции дифференцируются с помощью ряда правил и формул.
Правила дифференцирования:
Формулы для вычисления производной:
1.Вычислите производную функций: 1) 6) 11) 2. Найти значение производной функции 3. Дано: 4. Решить уравнение 5. Найти угловой коэффициент касательной к графику функции 6. Найти тангенс угла наклона касательной к графику функции 7. Решить неравенство 8. Найти 9. При каких х производная функции 10. В какой точке угловой коэффициент касательной к графику функции 11. В каких точках касательная к кривой 12. Составить уравнение касательной к графику к функции | ||||||||||||||||||||||||||||||||||||||||||||||||
4. Производная сложной функции.
Пусть 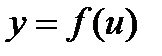 и
и 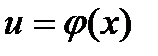 , тогда
, тогда 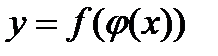 - сложная функция с промежуточным аргументом u и независимым аргументом х.
- сложная функция с промежуточным аргументом u и независимым аргументом х.
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Получим 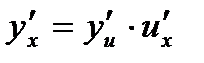 .
.
Пример 1.Найти производную функции 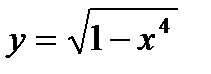 .
.
Решение:Данная функция является сложной. Ее можно представить в виде простых
функций: 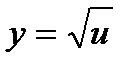 , где
, где 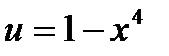 . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции 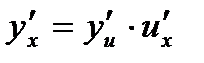 ,получаем
,получаем 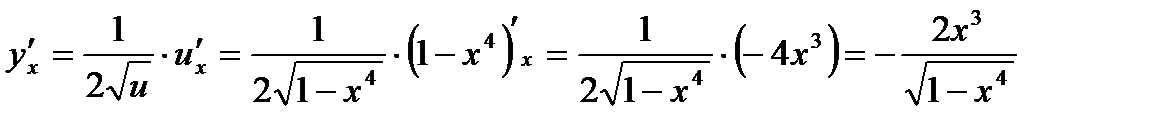 .
.
Пример 2.Найти производную функции 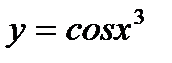 .
.
Решение:Данная функция является сложной. Ее можно представить в виде простых функций: 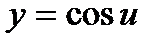 , где
, где 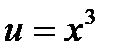 . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции 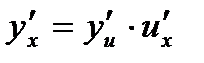 ,получаем
,получаем 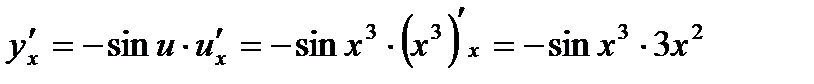 .
.
| Функция | Производная |
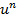
| 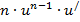
|

| 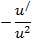
|
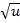
| 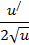
|
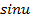
| 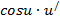
|
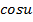
| 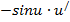
|
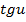
| 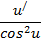
|
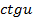
| 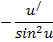
|
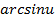
| 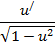
|
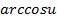
| 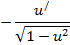
|
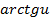
| 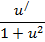
|
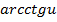
| 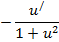
|
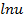
| 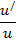
|
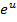
| 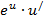
|
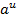
| 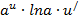
|
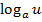
| 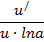
|
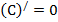
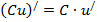
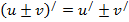
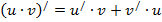
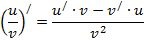
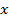
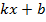
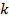
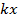
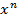
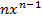

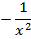
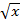
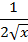
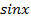
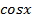
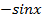
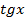
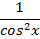
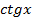
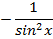
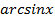
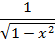
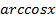
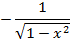
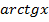
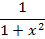
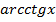
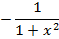
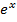
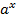
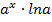
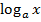
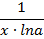
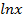
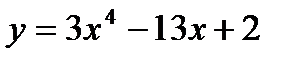 ; 2)
; 2) 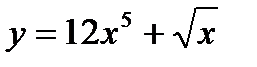 ; 3)
; 3) 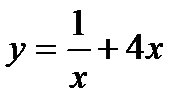 ; 4)
; 4) 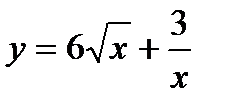 ; 5)
; 5) 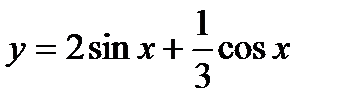 ;
; 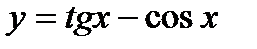 ; 7)
; 7) 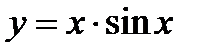 ; 8)
; 8) 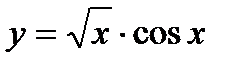 ; 9)
; 9) 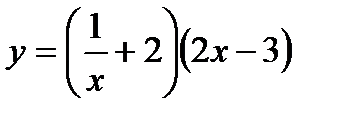 ; 10)
; 10) 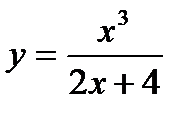 ;
;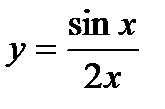 .
.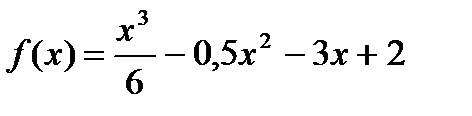 в точке
в точке 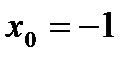
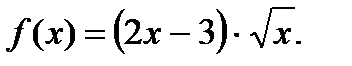 Найти
Найти 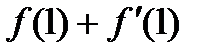 .
.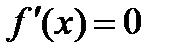 , если
, если 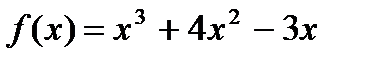
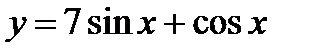 в точке
в точке 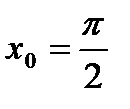 .
.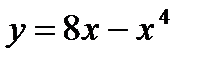 в точке
в точке 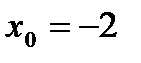 .
.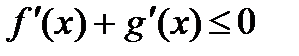 , если
, если 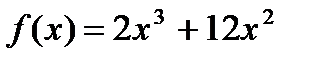 ,
, 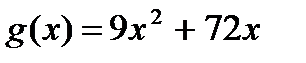 .
.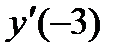 , если
, если 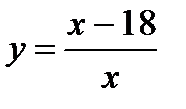 .
.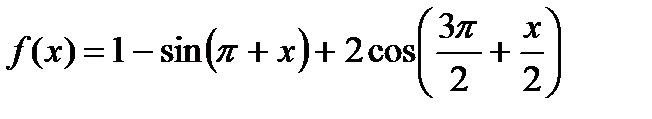 равна нулю?
равна нулю?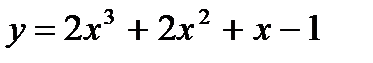 равен 3?
равен 3?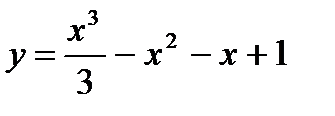 параллельна прямой
параллельна прямой 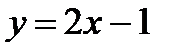 .
.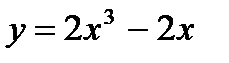 в точке
в точке 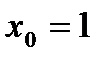 .
.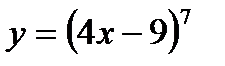 ; 2)
; 2) 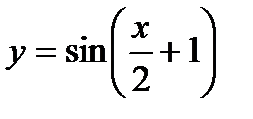 ; 3)
; 3) 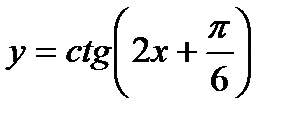 ; 4)
; 4) 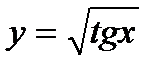 ; 5)
; 5) 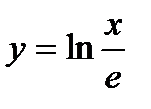 ;
; 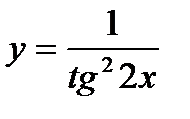 ; 7)
; 7) 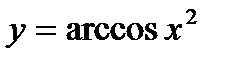 ; 8)
; 8) 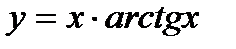 ; 9)
; 9) 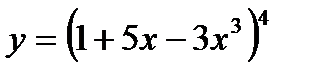 ; 10)
; 10) 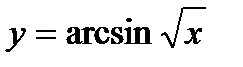 ; 11)
; 11) 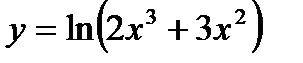 ; 12)
; 12) 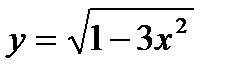 ; 13)
; 13) 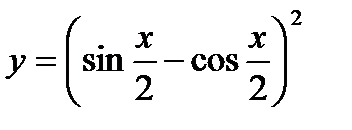 ; 14)
; 14) 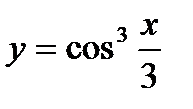 ;
; 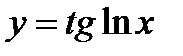 ; 16)
; 16) 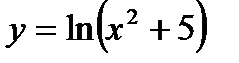 ; 17)
; 17) 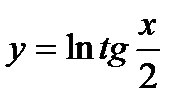 ; 18)
; 18) 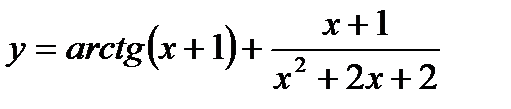 ;
;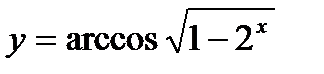 ; 20)
; 20) 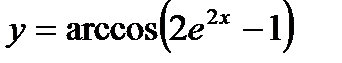 ; 21)
; 21) 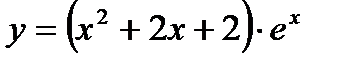 ; 22)
; 22) 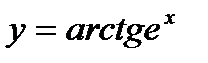 .
.