Финансовые функции.

Финансовые функции.

В основе расчетов, выполняющихся с использованием финансовых функций Microsoft Excel, лежит несколько специальных формул, которые базируются на принципе сложных процентов. Для исчисления характеристик финансовых операций с элементарными потоками платежей используют функции БС() [БЗ()], КПЕР(), СТАВКА() [НОРМА()], ПС() [ПЗ()], ПЛТ() [ППЛАТ()].

1. Функция БС вычисляет будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки (онаподходит для расчета итогов накоплений при ежемесячных банковских взносах).

Синтаксис: БС(Ставка; Кпер; Плт; Пс; Тип).

Ставка- это процентная ставка за период.

Кпер - это общее число периодов выплат годовой ренты.

Плт - это выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно плата состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если аргумент опущен, должно быть указано значение аргумента Пс.

Пс- это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента. Если аргумент опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента Плт.

Тип - это число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода, 1 - в начале периода). Если аргумент опущен, то он полагается равным 0.

Замечание: для аргументов Ставка и Кпер используются согласованные единицы измерения. Если производятся ежемесячные платежи по четырехгодичному займу из расчета 12% годовых, то Ставка должна быть 12%/12, а Кпер должно быть 4*12. Если производятся ежегодные платежи по тому же займу, то Ставка должна быть 12%, а Кпер должно быть 4.

Все аргументы, означающие деньги, которые вы платите (например, депозитные вклады), представляются отрицательными числами; деньги, которые вы получаете (например, дивиденды), представляются положительными числами.

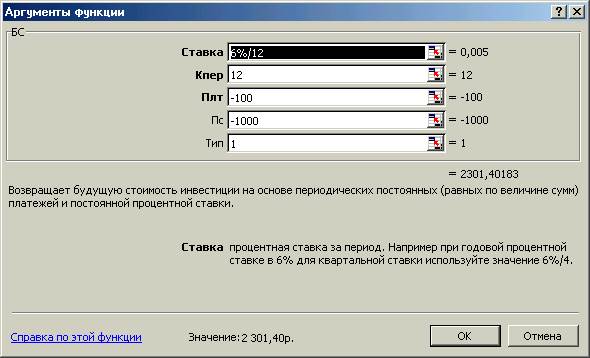
Пример: Вы собираетесь вложить 1000 руб. под 6% годовых (что составит в месяц 6%/12 или 0,5%) и собираетесь вкладывать по 100 руб. в начале каждого месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?

БС (0,5%; 12; -100; -1000; 1). Результат 2301,40 руб.

Для выполнения расчета вызывается Мастер функций, в поле Категории выбираются финансовые функции и в поле Функция выбирается функция БС. В появившемся окне заполняются соответствующие поля путем подстановки значений аргументов, а если данная функция вычисляется в расчете, то вместо этого указываются адреса исходных данных из таблицы расчета.

Для определения срока платежа и процентной ставки используются функции КПЕР и СТАВКА [НОРМА].

2. Функция КПЕР вычисляет общее число периодов выплат как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной процентной ставки. Если платежи производятся несколько раз в год, то для того, чтобы найти число лет выплат, общее число периодов надо разделить на число периодов в году.

Синтаксис: КПЕР (Ставка; Плт; Пс; Бс; Тип).

Ставка - это процентная ставка за период.

Плт - выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам, никакие другие сборы или налоги не учитываются.

Пс – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.

Бс - это будущая стоимость, или баланс наличности, который должен быть достигнут после последней выплаты. Если аргумент опущен, то предполагается, что он равен 0.

Тип - это число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода, 1 - в начале периода).

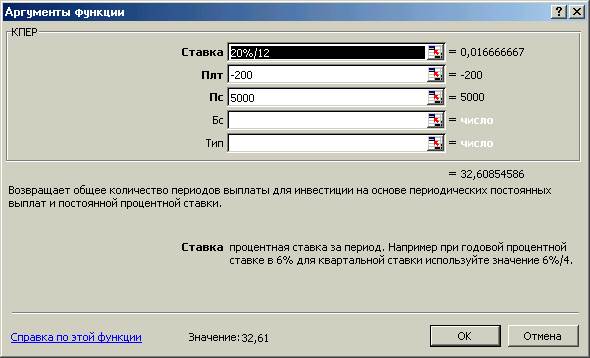
Пример: рассчитаем срок погашения ссуды размером 5000 руб., выданной под 20% годовых при погашении ежемесячными платежами по 200 руб.

КПЕР (20%/12; -200; 5000). Результат 32,6 месяца или 2,7 года.

3. Функция СТАВКА определяет значение процентной ставки за один расчетный период, т.е. возвращает процентную ставку по аннуитету за один период (поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют финансовой рентой или аннуитетом). Для нахождения годовой процентной ставки полученное значение необходимо умножить на число расчетных периодов в году.

Функция СТАВКА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Если после 20 итераций погрешность определения ставки превышает 0,0000001, то функция СТАВКА возвращает сообщение об ошибке #ЧИСЛО!.

Синтаксис: СТАВКА (Кпер; Плт; Пс; Бс; Тип; Предположение).

Кпер - общее число периодов платежей по аннуитету.

Плт - регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно Плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов и налогов. Если аргумент опущен, должно быть указано значение аргумента Бс.

Пс - приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.

Бс - требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, то он полагается равным 0.

Тип - число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода, 1 - в начале периода).

Предположение - предполагаемая величина ставки. Если значение предположения опущено, то оно полагается равным 10 процентам. Если функция СТАВКА не сходится, попробуйте подставить различные значения для предположения. СТАВКА обычно сходится, если величина предположения находится между числами 0 и 1.

Замечание: Убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов прогноз и кол_пер. Если делаются ежемесячные выплаты по четырехгодичному займу под 12 процентов годовых, используйте 12%/12 для задания аргумента прогноз и 4*12 для задания аргумента кол_пер. Если делаются ежегодные платежи по тому же займу, то используйте 12% для задания аргумента прогноз и 4 для задания аргумента кол_пер.

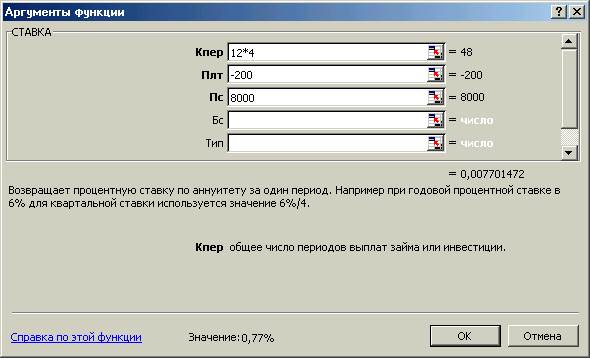
Пример: надо определить процентную ставку для четырехлетнего займа в 8000 руб. с ежемесячной выплатой в 200 руб.

СТАВКА (12*4; -200; 8000). Результат 0,0077, или 0,77% в месяц (округляется до 1%). Годовая процентная ставка по займу будет равна СТАВКА (4*12; -200; 8000)*12 = 9,24%.

4. Функция ПС - возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на настоящий момент равноценна ряду будущих выплат. Например, когда вы занимаете деньги, сумма займа является приведенной (нынешней) стоимостью для заимодавца.

Синтаксис: ПС(Ставка; Кпер; Плт; Бс; Тип)

Ставка - процентная ставка за период (например, если получена ссуда на автомобиль под 10 процентов годовых и делаются ежемесячные выплаты, то процентная ставка за месяц составит 10%/12 или 0,83%).

Кпер - общее число периодов платежей по аннуитету (например, если получена ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то ссуда имеет 4*12 или 48 периодов).

Плт - выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включает других сборов или налогов (например, ежемесячная выплата по четырехгодичному займу в 10 000 руб. под 12 процентов годовых составит 263,33 руб. В качестве значения аргумента выплата нужно ввести в формулу число -263,33).

Бс - требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0. Например, если предполагается накопить 50000 руб. для оплаты специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая стоимость. Можно сделать предположение о сохранении заданной процентной ставки и определить, сколько нужно откладывать каждый месяц.

Тип - число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода, 1 - в начале периода).

Замечание: убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов ставка и кпер. Если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, то используйте 12%/12 для задания аргумента ставка и 4*12 для задания аргумента кпер. Если Вы делаете ежегодные платежи по тому же займу, то используйте 12% для задания аргумента ставка и 4 для задания аргумента кпер.

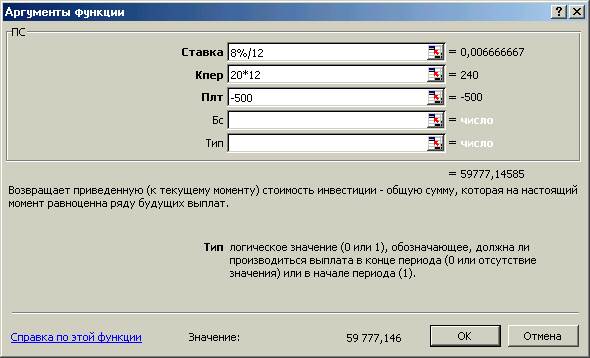
Пример: просят инвестировать в проект 60000 руб. и будут возвращать по 500 руб. в начале каждого месяца в течении 20 лет. Будет ли выгодна эта сделка при ставке 8% в год (Нет, т.к. возвратят всего 59777,14 руб.).

5. Функция ПЛТ - возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.

Синтаксис: ПЛТ(Ставка; Кпер; Пс; Бс; Тип).

Ставка - процентная ставка по ссуде.

Кпер - общее число выплат по ссуде.

Пс - приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.

Бс - требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент опущен, то он полагается равным 0 (нулю).

Тип - число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода, 1 - в начале периода).

Замечание: выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой. Убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов ставка и кпер. Если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, то используйте 12%/12 для задания аргумента ставка и 4*12 для задания аргумента кпер. Если вы делаете ежегодные платежи по тому же займу, то используйте 12 процентов для задания аргумента ставка и 4 для задания аргумента кпер.

Пример_1: Вы взяли кредит 10000 руб. сроком на 10 месяцев. Какова должна быть сумма месячного платежа по указанному кредиту при годовой процентной ставке 8% (-1037,03).

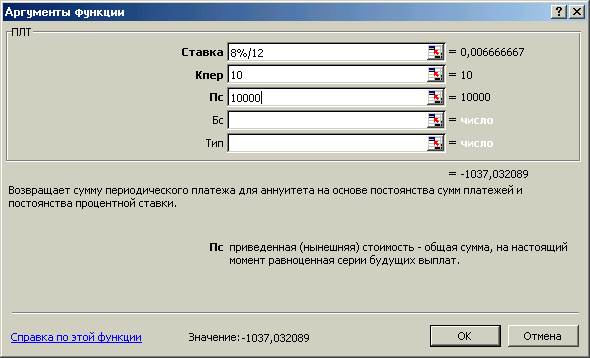
Пример 2: определите необходимую сумму месячного платежа для получения 50 000 руб. в конце восемнадцатилетнего периода (-129,08)

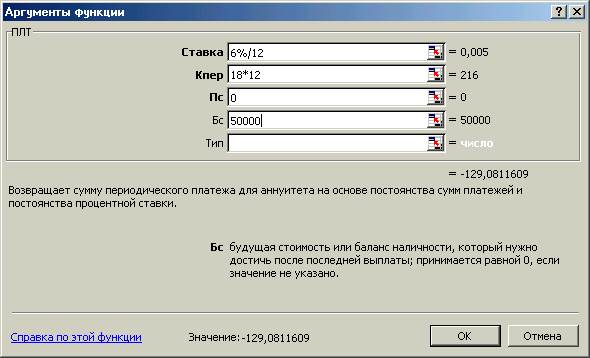
6. Функция БЗ - предназначена для расчета будущей стоимости периодических постоянных платежей и единой суммы вклада или займа на основе постоянной процентной ставки(подходит для расчета итогов накоплений при ежемесячных банковских взносах). Замечание: рекомендуется функция БС.

Синтаксис: БЗ (Норма; Кпер; Плата; Нз; Тип).

Норма - процентная ставка за период.

Кпер - общее число периодов выплат годовой ренты.

Плата - выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно плата состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов.

Нз - текущая стоимость, или общая сумма всех будущих платежей с настоящего момента (если аргумент опущен, то он полагается равным 0).

Тип - число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода, 1 - в начале периода). Если аргумент опущен, то он полагается равным 0.

Пример: предположим, вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год и собираетесь вложить 1000 руб. при годовой ставке 6%. Вы собираетесь вкладывать по 100 руб. в начале каждого месяца в течение года. Сколько денег будет на счете в конце 12 месяцев? БЗ(6%/12; 12; -100; -1000; 1). Получаем ответ: 2301,40 руб.

7. Функция НОРМА - определяет значение процентной ставки за один расчетный период. Для нахождения годовой процентной ставки полученное значение необходимо умножить на число расчетных периодов в году. Функция НОРМА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Если после 20 итераций погрешность определения ставки превышает 0,0000001, то функция НОРМА возвращает значение ошибки #ЧИСЛО!. Замечание: рекомендуется функция СТАВКА.

Синтаксис: НОРМА (Кпер; Выплата; Нз; Бз; Тип; Нач прибл).

Кпер - общее число периодов выплат.

Выплата - величина постоянных периодических платежей.

Нз - текущее значение, т.е. общая сумма, которую составят будущие платежи.

Бс - будущая стоимость, или баланс наличности, который нужно достичь после последней выплаты (если аргумент опущен, он полагается равным 0).

Нач прибл - предполагаемая величина нормы. Если Нач прибл опущено, то оно полагается равным 10%. Если функция НОРМА не сходится, следует попытаться использовать различные значения Нач прибл. Обычно функция НОРМА сходится, если Нач прибл имеет значение между 0 и 1. Пример: надо определить процентную ставку для четырехлетнего займа в 8000 руб. с ежемесячной выплатой в 200 руб. НОРМА (48; -200; 8000). Результат: процентная ставка за месяц равна 0,77% или 9,24% годовых.

8. Функция ПЗ - предназначена для расчета текущей стоимости как единой суммы вклада (займа), так и будущих фиксированных периодических платежей (возвращает текущий объем вклада на основе постоянных периодических платежей). Денежные взносы в функции ПЗ должны быть постоянными на весь период инвестиции. Этот расчет является обратным по отношению к будущей стоимости (БЗ). Замечание: рекомендуется функция ПС.

Синтаксис: ПЗ(Норма; Кпер; Выплата; Бс; Тип)

Норма - процентная ставка за период.

Кпер - общее число периодрв выплат

Выплата - величина постоянных периодических платежей.

Пример: фирме потребуется 5000 тыс.руб. через 12 лет. В настоящее время фирма располагает деньгами и готова положить их на депозит единым вкладом, чтобы через 12 лет он достиг 5000 тыс.руб. Определим необходимую сумму текущего вклада, если ставка процента по нему составляет 12% в год. Для расчета используется формула: ПЗ(12%,12,,5000)= -1283,38 тыс.руб.

8. Функция ППЛАТ - вычисляет величину выплаты за один период на основе фиксированных периодических выплат и постоянной процентной ставки (например, регулярных платежей по займу). Замечание: рекомендуется функция ПЛТ.

Синтаксис: ППЛАТ(Норма; Кпер; Нз; Бс; Тип)

Норма - процентная ставка за период.

Кпер - общее число периодов выплат.

Нз - текущее значение, т.е. общая сумма, которую составят будущие платежи.

Пример: Предположим, что необходимо накопить 4000 тыс.руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых. Решение: Общее число периодов вкладов составляет 3*12 (аргумент кпер) и ставка процента за период 12%/12 (аргумент норма). Аргумент тип=0, так как вклады будут производиться в конце месяца. Величина ежемесячных выплат: ППЛАТ(12%/12,12*3,,4000)= -92,86 тыс.руб.