МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Нижегородский государственный педагогический университет имени Козьмы Минина

Кафедра «Математики»

Индивидуальный творческий проект

на тему:

Математическая модель всплытия

подводной лодки

Выполнил:

студент группы ПКС-11 курса 3

Семеновых М.А.

Проверил:

Преподаватель Вильданов В.К.

Нижний Новгород

2014 год

Содержание

1. Введение…………………………………………………………3

2. История вопроса………………………………………………...4

3. Математическая модель………………………………………..5

4. Компьютерная модель……………………………………….....7

5. План экспериментов……………………………………………8

6. Вывод…………………………………………………………..13

Список используемой литературы…………………………...14

Введение.

Под словами математическая модель всплытия подводной лодки подразумевается описание физического процесса, происходящего при её всплытии с некоторой глубины. Естественно, математическая модель существенно отличается от реально происходящего процесса, так как при построении модели берется приближение, при котором пренебрегают некоторыми силами и факторами среды.

В данном случае, вместо лодки, идущей на какой-то глубине, рассматривается материальная точка с переменной массой. Мы будем пренебрегать гидродинамикой этого процесса рассматривая только три основных силы действующих на эту точку (сила Архимеда, сила притяжения, сила сопротивления).

Рассматривая, таким образом, действия сил на объект, используя основные законы механики и соотношения между силами мы можем составить дифференциальное уравнение или систему дифференциальных уравнений, решая которую, можно получить её частное или общее решение (в зависимости от вида системы).

Получив решение, мы можем ответить и на другие вопросы, касающиеся всплытия лодки, такие, как нахождение значений параметров при которых время всплытия лодки будет минимальным, и ряд других.

На идее моделирования, по существу, базируется любой метод исследования – как теоретический(при котором используются абстрактные модели), так и экспериментальный (использующий предметные модели).

Построение математической модели процесса позволяет понять его суть и его физический смысл.

История вопроса

Создание подводной лодки - замечательное достижение человеческого разума и значительное событие в истории военной техники.

Подводный корабль, как известно, обладает способностью действовать скрытно, невидимо, а следовательно, внезапно. Скрытность достигается, прежде всего, способностью погружаться, плавать на определенной глубине, не выдавая своего присутствия, и неожиданно наносить удары противнику.

Как и всякое физическое тело, подводная лодка подчиняется закону Архимеда, который гласит, что на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной телом жидкости. Можно для упрощения сформулировать этот закон так: «Тело, погруженное в воду, теряет в своем весе столько же, сколько весит вытесненный телом объем воды». Именно на этом законе основано одно из главных свойств любого корабля - его плавучесть, то есть способность удерживаться на поверхности воды. Это возможно тогда, когда вес воды, вытесненной погруженной в воду частью корпуса, равен весу судна. При таком положении корабль обладает положительной плавучестью. Если же вес вытесненной воды меньше веса корабля, то корабль будет тонуть. В этом случае считают, что корабль обладает отрицательной плавучестью.

Для подводной лодки плавучесть определяется ее способностью находиться как в подводном, так и в надводном положении. Очевидно, лодка будет находиться на поверхности, если она имеет положительную плавучесть. Получая отрицательную плавучесть, лодка будет погружаться, пока не ляжет на дно. Чтобы она не стремилась ни всплыть, ни тонуть, необходимо уравнять вес подводной лодки и вес вытесняемого ей объема воды. В этом случае лодка без хода займет в воде неустойчивое безразличное положение и будет «висеть» на любой глубине. Это значит, что лодка получила нулевую плавучесть.

Чтобы подводная лодка могла погружаться, всплывать или держаться под водой, она должна обладать способностью менять свою плавучесть. Это достигается очень простым способом - принятием на лодку водяного балласта: специальные цистерны, устроенные в корпусе лодки, то заполняются забортной водой, то вновь опорожняются. При их полном заполнении лодка обретает нулевую плавучесть. Чтобы подводная лодка всплыла, надо освободить цистерны от воды.

Однако регулировка погружения с помощью цистерн никогда не может быть точной. Маневрирование в вертикальной плоскости достигается при помощи перекладки горизонтальных рулей. Как самолет в воздухе способен менять высоту полета при помощи рулей высоты, так и подлодка действует горизонтальными рулями или рулями глубины, не меняя плавучести. Если передняя кромка пера руля выше задней, набегаемый поток воды будет создавать подъемную силу, направленную вверх. И наоборот, если передняя кромка руля ниже задней, встречный поток будет давить на рабочую поверхность пера сверху вниз. Изменение направления движения подлодки в горизонтальном положении производится у подлодок, как и у надводных кораблей, изменением угла поворота вертикального руля.[3]

Математическая модель

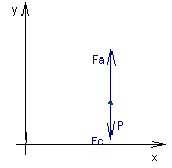
Рассмотрим подводную лодку как материальную точку, которая движется по вертикали на некоторой глубине, с некоторой постоянной скоростью. Лодка удифферентована, то есть силы, которые действуют на лодку по вертикали, как показано на рис.1, (сила тяжести и выталкивающая сила Архимеда) равны по модулю.

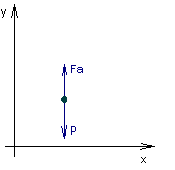По вертикали, на лодку действует сила сопротивления, модуль которой примем в виде:

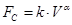
Где степень 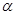и коффициент пропорциональности 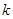это некоторые числа, характерные для данной среды, и зависящие от факторов среды, таких как: плотность

Рис. 1 воды, её температура, и величины скорости.[4]

Сила Архимеда, действующая на лодку, зависит от размеров лодки, а именно от её объема, и плотности воды.

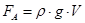
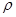В этой формуле – это плотность жидкости, 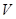–объем тела, погруженного в жидкость, = 9.81 м / c² – ускорение свободного падения.

Пусть в некоторый момент времени выключены двигатели и сбрасывается балласт. Двигаясь по инерции, а также под действием силы Архимеда, она начнет всплывать по некоторой траектории (рис.2). [2]

Рис. 2

Силу сопротивления мы можем записать так:

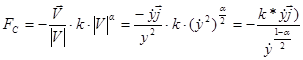
так как вектор скорости всегда направлен по касательной к траектории движения, а сила сопротивления имеет противоположное направление.

По второму закону Ньютона:

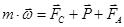где вектор 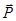- это вектор силы тяжести, действующей на лодку. 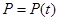- некоторая функция зависящая от времени. [5]

Запишем это векторное уравнение в проекциях на оси.

В проекции на ось :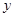

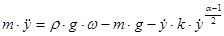
где масса 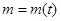- функция зависящая от времени. Решая эту систему для произвольного значения 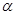, и заданных начальных условий, мы получим уравнение траектории движения подводной лодки.

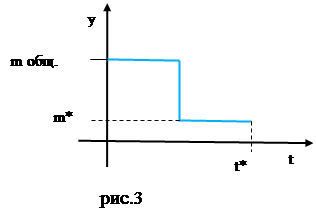Пусть масса лодки изменится мгновенно. 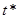- некоторый момент времени, в который вся вода из цистерн вытеснена. Как показано на рис.3, в некоторый момент времени m_воды будет равняться 0, и мы получим 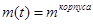, то – есть, вся вода из цистерн будет вытеснена.

В результате выше написанного мы можем привести математическую модель к общему виду для того, что бы решить ее на ЭВМ.

V=V₀+at y=y₀+V₀t+at²/2

F=ma F=-mg+F_a-R

a=F/m R=kV_y²

Компьютерная модель

Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модель объединяются в таблицу, которая содержит три области:

- исходные данные;

- промежуточные расчеты;

- результаты.

1. Заполните область исходных данных.

2. Заполните расчетные столбцы A, B, C и D, в которых вычисляются параметры всплытия подводной лодки:

- время;

- скорость;

- масса;

- ускорение.

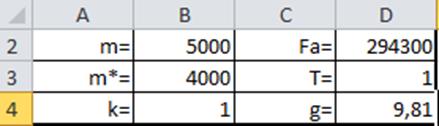
3. Введите формулы в расчетные ячейки.

Ячейка	Формула
D2	=B1D4D1
В9	=B8+C8$D$3+(D8$D$3^2)/2
С9	=C8+D8*$D$3
D9	=E9/$B$2
E9	=-$B$2$D$4+$D$2-$B$4C9^2

План экспериментов

Эксперимент №1

Исследовать всплытие под действием силы тяжести и сопротивления воды, проверка адекватности модели.

Подводная лодка всплывает с заданными в таблице характеристиками.

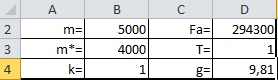
Сравниваем результаты тестового расчета с качественной моделью.

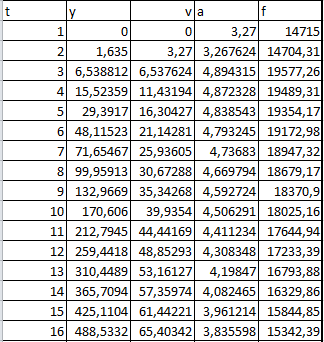
График траектории всплытия подводной лодки.

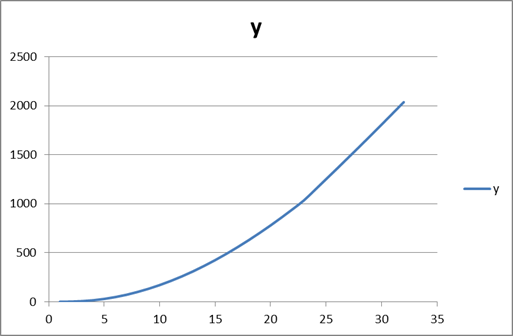
График изменения скорости.

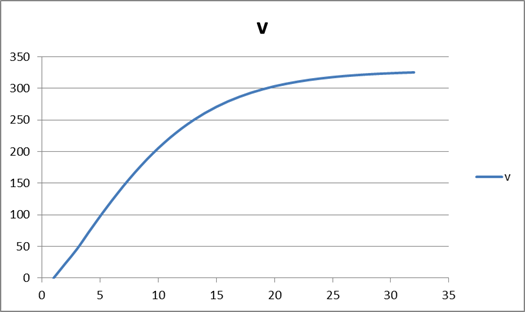
Вывод: данная модель адекватна, так как при ускорение всплытия подводной лодки уменьшается, а скорость достигая предельной становится равномерной. Так же при сбросе балласта мы можем заметить как возросло ускорение. По данной математической модели максимальная скорость всплытия подводной лодки равна 33 узлам. Возьмем для сравнения подводную лодку «Комсомолец».[6] Её подводная скорость равна 31 узел, что схоже c нашей. Следовательно математическая модель адекватна.

Эксперимент №2

Исследовать зависимость максимальной скорости всплытия подводной лодки от глубины ее погружения.

Подводная лодка всплывает с заданными в таблице характеристиками.

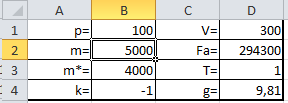
График скорости всплытия подводной лодки.

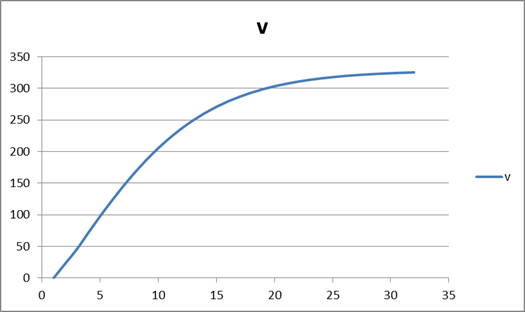
Вывод: по данной модели можно сказать, что чем меньше глубина, тем больше скорость всплытия подводной лодки.

Эксперимент №3

Исследовать минимальное время всплытие подводной лодки.

Подводная лодка всплывает с заданными в таблице характеристиками.

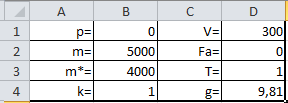
График траектории всплытия подводной лодки.

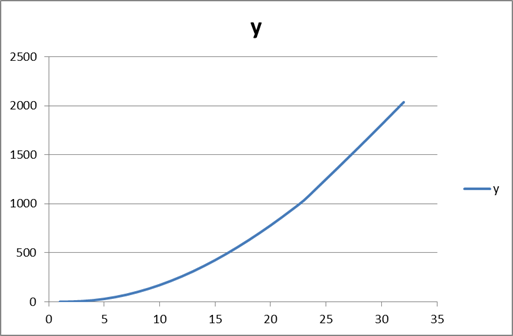
Вывод: по данной модели можно сказать, что минимальное время всплытия подводной лодки с 1000 метров равно 23 минутам. Срочное всплытие производится в аварийных и некоторых других случаях. При срочном всплытии подводная лодка всплывает в надводное положение или на заданную глубину в минимальное время, не задерживаясь на промежуточных глубинах, а продувание цистерн главного балласта производится воздухом высокого давления. При этом в зависимости от обстановки продуваются только средняя группа или средняя и одна из концевых, или все группы.

Заключение.

Мы рассмотрели только частные случаи решения задачи с использованием ЭВМ.

Но, уже по частным случаям решений, можно увидеть некоторую закономерность, на основании которых, уже можно делать какие-то выводы.

Сам процесс всплытия подводной лодки – достаточно сложный физический процесс. На всплытие лодки влияют не только несколько сил действующие на неё. Большое значение имеют гидродинамические параметры, которые в построении данной модели не учитывались. Для численных решений системы и построения графиков были взяты реальные размеры и начальная скорость подводной лодки, что позволило как можно больше приблизить рассмотренный процесс к реальному.

Список литературы.

1. Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения

М.: Изд-во МГТУ имени Н.Э. Баумана, 2000. - 347 с.

2. Степанов В.В. Курс дифференциальных уравнений

М.: Изд-во технико-теоретической литературы, 1950. - 467 с.

3. Осипенко Л., Жильцов Л., Мормуль Н. Атомная подводная эпопея

М.: “Боргес”, 1994. - 350 c.

4. http://physics-animations.com/newboard/themes/78296.html

5. http://www.math24.ru/newtons-second-law-of-motion.html

6. http://ru.wikipedia.org/wiki/%CA%EE%EC%F1%EE%EC%EE%EB%E5%F6_(%EF%EE%E4%E2%EE%E4%ED%E0%FF_%EB%EE%E4%EA%E0)