Контакты

Случайная статья

ЛиНУрФ. Лекция 19.01.2021. Сферические функции и их свойства. Применение сферических функций к решению задач. Внутренняя 1-я краевая задача (Дирихле). Внешняя 1-я краевая задача (Дирихле). Внутренняя 2-я краевая задача (Неймана). Внешняя 2-я краевая задач

ЛиНУрФ. Лекция 19.01.2021

27. Сферические функции и их свойства

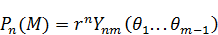– однородный гармонический полином.

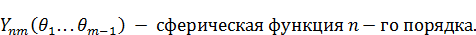
Максимальное число независимых переменных определяется как:

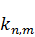
Например: 1) .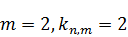

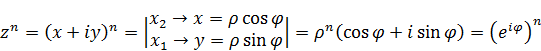
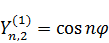
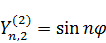
2) .

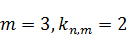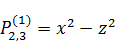
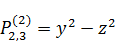
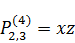
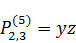
Переход к сферическим координатам:

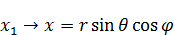
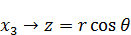
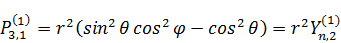
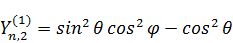
Основные свойства сферических функций

1) Любая сферическая функция представляет собой многочлен, состоящий из .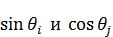

2) Свойство ортогональности сферических функций.

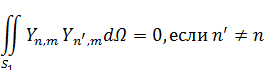
3. Для 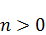существует 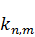линейно независимых сферических функций.

4. 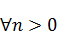можно проделать процедуру ортогонализации и после этого нормировать на единицу.

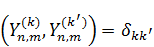
5. Свойство полноты. Система функций является полной в пространстве функций 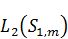в пределах сферы радиуса 1. 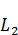– функции, которые интегрируем с их квадратом. .

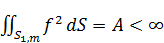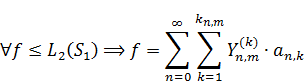
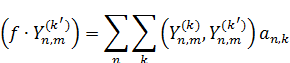
6) 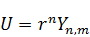удовлетворяет уравнению Лапласа в любой конечной области.

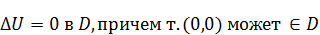
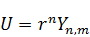– может являться решением уравнения Лапласа (шаровая функция).

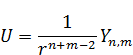
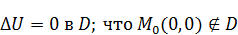
28. Применение сферических функций к решению задач

Рассмотрим первую краевую задачу в сфере.

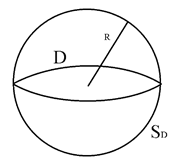
Внутренняя 1-я краевая задача (Дирихле)

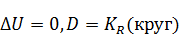
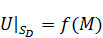
На границе . . .

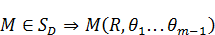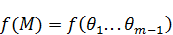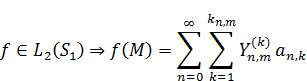
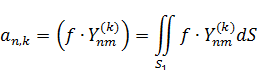
Внешняя 1-я краевая задача (Дирихле)

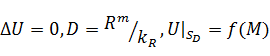
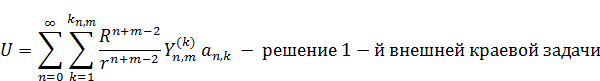
Внутренняя 2-я краевая задача (Неймана)

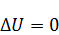
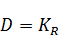
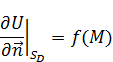
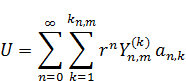
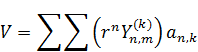
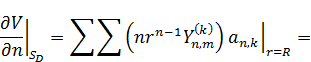
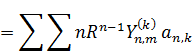
Решением задачи Неймана будет являться такая функция:

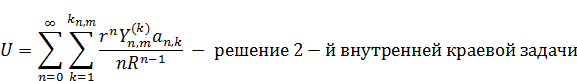
Внешняя 2-я краевая задача (Неймана)

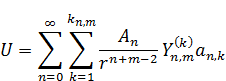
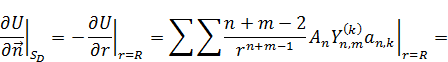
Необходимо, чтобы 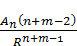равнялось единице. Значит:

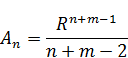
И тогда решение краевой задачи:

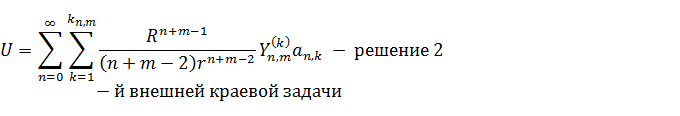
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.