
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Обратная матрица. Найти:
1. Обратная матрица. Найти:
Решение: 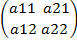
| a. | 2. | 3. | 4. | 5. | 6. |
2. Решить систему: 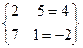
 методом Гаусса:
методом Гаусса:
Решение:
Ваша матрица
| № | X1 | X2 | b |
| -2 |
Получили единицу в 1-ом столбце разделив 1-ую строку на 2
| № | X1 | X2 | b |
| 5/2 | |||
| -2 |
Занулили 1-ый столбец
| № | X1 | X2 | b |
| 5/2 | |||
| -33/2 | -16 |
Получили единицу в 2-ом столбце разделив 2-ую строку на -33/2
| № | X1 | X2 | b |
| 5/2 | |||
| 32/33 |
Занулили 2-ой столбец
| № | X1 | X2 | b |
| -14/33 | |||
| 32/33 |
3. Решить систему:  по правилу Крамера:
по правилу Крамера:
Решение:
Ваша матрица
| № | X1 | X2 | X3 | b |
Выписали основную матрицу и нашли ее определитель
| № | X1 | X2 | X3 |
D = 19
Подставили столбец решений в 1-ый столбец основной матрицы и нашли ее определитель
| № | X1 | X2 | X3 |
D1 = 14
Подставили столбец решений в 2-ой столбец основной матрицы и нашли ее определитель
| № | X1 | X2 | X3 |
D2 = 68
Подставили столбец решений в 3-ий столбец основной матрицы и нашли ее определитель
| № | X1 | X2 | X3 |
D3 = 6
x1 = D1 / D = 14 / 19 = 14/19
x2 = D2 / D = 68 / 19 = 68/19
x3 = D3 / D = 6 / 19 = 6/19
4. Основная теорема алгебры. Разложение на множители многочленов над  :
:
Основна́я теоре́ма а́лгебры утверждает, что Всякий отличный от константы многочлен (от одной переменной) комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
Эквивалентная формулировка теоремы следующая: Поле комплексных чисел алгебраически замкнуто.
5. Как представить комплексное число матрицей второго порядка:
Каждому комплексному числу 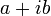 (С действительными
(С действительными 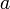 и
и 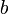 ) Можно поставить в соответствие квадратную матрицу 2-го порядка вида
) Можно поставить в соответствие квадратную матрицу 2-го порядка вида 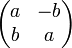 . Такое соответствие задает изоморфизм между системой комплексных чисел и системой матриц такого вида, если сложению, вычитанию и умножению комплексных чисел поставить в соответствие обычные сложения, вычитания и умножения матриц. Легко видеть, что в этом представлены операции комплексного сопряжения соответствует транспонирования матрицы. Настоящая единица представляется как единичная матрица
. Такое соответствие задает изоморфизм между системой комплексных чисел и системой матриц такого вида, если сложению, вычитанию и умножению комплексных чисел поставить в соответствие обычные сложения, вычитания и умножения матриц. Легко видеть, что в этом представлены операции комплексного сопряжения соответствует транспонирования матрицы. Настоящая единица представляется как единичная матрица 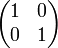 , А мнимая единица - как
, А мнимая единица - как 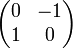 .
.
Нетрудно проследить, что действительно вышеуказанные арифметические действия дают соответствующие результаты при выполнении их над числами и над соответствующими матрицами (что и доказывает изоморфность этих структур):
-
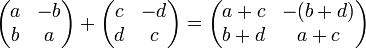 , Что соответствует действия
, Что соответствует действия 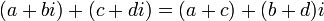 .
.
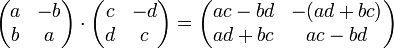 , Что соответствует действия
, Что соответствует действия 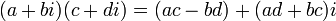 .
.
6. Формула Муавра:
Формула Муаврадля комплексных чисел 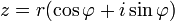 утверждает, что
утверждает, что 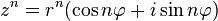 для любого
для любого 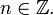
7. Решение двучленных уравнений: 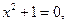
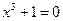 и
и 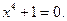 :
:
Решение:
8. Изображение на комплексной плоскости корней 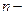 ой степени из числа
ой степени из числа 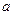 . Изобразите
. Изобразите 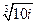 :
:
9. Тригонометрическая форма комплексного числа. Умножение и деление чисел в тригонометрической форме:
Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть 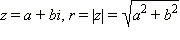 и φ = arg z. Тогда по определению аргумента имеем:
и φ = arg z. Тогда по определению аргумента имеем:
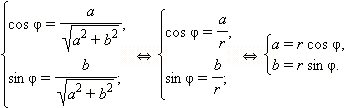
|
| Отсюда получается z = a + bi = r(cos φ + i sin φ |
10. Теорема Безу:
Если многочлен 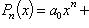
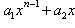
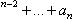 разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn(a).
разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = Pn(a).
11. Найти 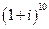 :
:
Решение:
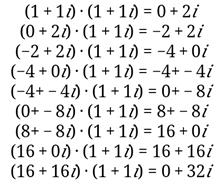
12. При каких 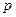
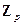 является полем, что это такое:
является полем, что это такое:
13. Найти: 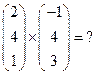
Решение:
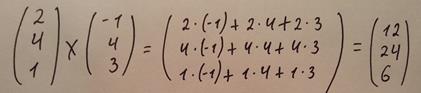
14. Матрицы и их свойства:
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
15. Определители, способы вычисления:
При вычислении определителей высокого порядка (больше 3-го) определение, как правило, не используется, так как это приводит к громоздким выражениям и требует большого количества арифметических операций. Гораздо эффективнее использовать свойства определителей. Наиболее важными для вычисления определителей являются свойства 3, 6, 9. Эти свойства можно назвать элементарными преобразованиями определителя, что соответствует элементарным преобразованиям матрицы.
I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.
II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.
III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.
16. Свойства определителей:
1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером.
2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.
3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
4. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
5. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.
17. Геометрический смысл определителей:
Если есть векторы с координатами (Ax, Ay) и (Вх, Ву), то площадь параллелограмма, построенного на этих векторах, равна определителю матрицы, столбцами которой являются эти векторы.
18. Правило Крамера:
Система линейных уравнений:
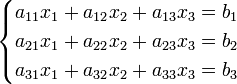
Определители:
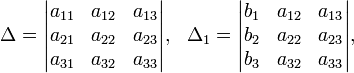
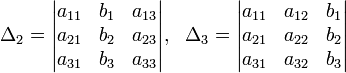
Решение:
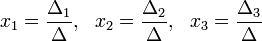
Пример:
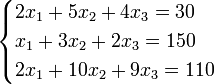
Определители:
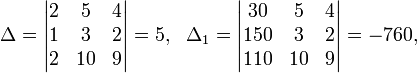
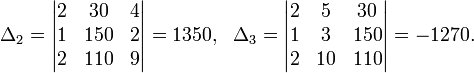
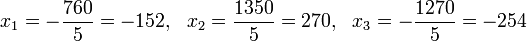
19. Метод Гаусса. Возможные завершения метода Гаусса:
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Покажем, как методом Гаусса можно решить следующую систему:
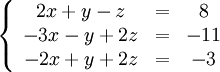
Обнулим коэффициенты при 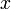 во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на
во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на 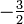 и
и 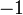 , соответственно:
, соответственно:
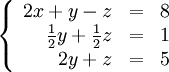
Теперь обнулим коэффициент при  в третьей строке, вычтя из неё вторую строку, умноженную на
в третьей строке, вычтя из неё вторую строку, умноженную на 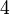 :
:
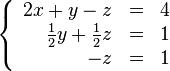
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
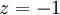 из третьего;
из третьего;
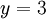 из второго, подставив полученное
из второго, подставив полученное 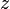
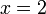 из первого, подставив полученные
из первого, подставив полученные 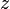 и
и  .
.
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
20. Теорема Кронекера-Капелли:
Теорема Кронекера-Капелли— критерий совместности системы линейных алгебраических уравнений. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
21. Теорема о ранге матрицы и базисном миноре:
Определение: Ранг матрицы А - максимальный порядок неравного нулю минора (минор - определитель квадратной матрицы 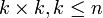 ). Обозначается
). Обозначается 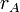 .
.
Определение: Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие БМ, назвыаются базисными строками и столбцами.
Определение: Система столбцов 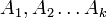 называется линейно зависимой
называется линейно зависимой 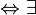 числа
числа 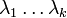 , не все равные нулю и такие что:
, не все равные нулю и такие что: 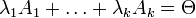
Теорема о базисном миноре: Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ.
22. Однородные системы линейных уравнений. Свойства их решений:
Однородной системойmлинейных уравнений сnнеизвестными называется система вида:
| (1) |
Эта система может быть записана в виде матричного уравнения
| A · X = O |
и операторного уравнения
| ^Ax = θ | (2) |
Система (1) всегда совместна, так как:
1. имеет очевидное решение x10 = x20 = … = xn0 = 0 , которое называется нулевым, или тривиальным;
2. добавление нулевого столбца не меняет ранга матрицы, следовательно, выполняется достаточное условие теоремы Кронекера–Капелли;
3. θ Î Img ^A , так как Img ^A — линейное пространство.
Естественно, нас интересуют нетривиальные решения однородной системы.
23. Линейные операторы на плоскости и в пространстве. Матрицы основных линейных операторов(поворота и растяжения):
Определение: Множество V называется векторным пространством (над полем действительных чисел R), если его элементы можно складывать между собой и умножать на действительные числа.
Определение: Отображение A: V → W двух векторных пространств V и W называется линейным оператором (действующим из V в W).
24. Векторное произведение определение и его вычисление:
Векторным произведением двух векторов 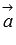 и
и 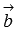 , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор
, заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор 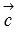 , что
, что
он является нулевым, если векторы 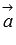 и
и 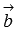 коллинеарны;
коллинеарны;
он перпендикулярен и вектору 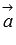 и вектору
и вектору 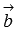 (
( 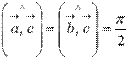 );
);
его длина равна произведению длин векторов 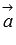 и
и 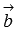 на синус угла между ними (
на синус угла между ними ( 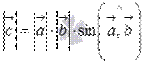 );
);
тройка векторов 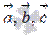 ориентирована так же, как и заданная система координат
ориентирована так же, как и заданная система координат
Найдите длину векторного произведения векторов 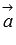 и
и 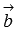 , если известно
, если известно 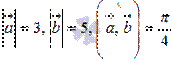 .
.
Решение:
Мы знаем из определения, что длина векторного произведения векторов 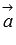 и
и 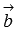 равна произведению длин векторов
равна произведению длин векторов 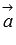 и
и 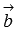 на синус угла между ними, поэтому,
на синус угла между ними, поэтому, 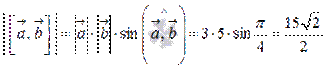 .
.
Ответ:
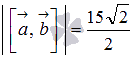
25. Смешанное произведение и его геометрический смысл:
Сме́шанное произведе́ние: 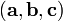 векторов
векторов 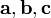 — скалярное произведение вектора
— скалярное произведение вектора  на векторное произведение векторов
на векторное произведение векторов 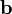 и
и  :
:
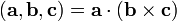 .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами  .
.
26. Скалярное произведение, его геометрический смысл и вычисление:
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю
27. Угол между прямыми на плоскости:
Определение: Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как:
Две прямые параллельны, если k1 = k2.
Две прямые перпендикулярны, если k1 = -1/k2.
Теорема: Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициентыА1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых
28. Найти: 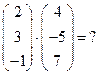
Решение:
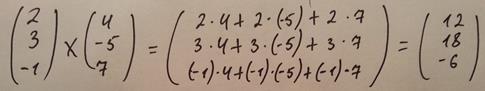
29. Найти угол между 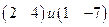 :
:
Решение:
30. Тригонометрическая форма комплексного числа 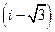 :
:
Найдём модуль этого числа: 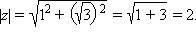 Аргумент данного числа находится из системы:
Аргумент данного числа находится из системы:
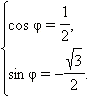
|
Значит, один из аргументов числа 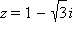 равен
равен 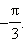
Получаем:
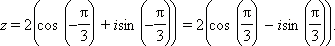
|
Ответ: 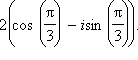
31. Тригонометрическая форма комплексного числа 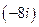 :
:
Ответ: 8 • [ cos ( 270° 0´ 0˝ ) + i • sin ( 270° 0´ 0˝ ) ]
32. Параметрическое уравнение прямой, проходящей через точки 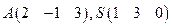 :
:
33. Виды уравнений прямой по плоскости:
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой.В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости, от каких – либо заданных начальных условий.
34. Найти нормаль к плоскости 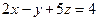 :
:
35. В кубе A,B,C,D, A1,B1,C1,D1; AA1 = i; AB = j; AD = k. Найти AB; AA1; AC1 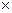 A1D:
A1D:
Решение:
36. Найти матрицу поворота на угол 60 градусов:
Решение:
37. Найти ранг матрицы 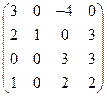 :
:
Решение:
Ваша матрица
| № | A1 | A2 | A3 | A4 |
| -4 | ||||
Занулили элементы в 1-ом столбце под 1-ым элементом
| № | A1 | A2 | A3 | A4 |
| -4 | ||||
| 8/3 | ||||
| 10/3 |
Занулили элементы в 3-ем столбце под 3-им элементом
| № | A1 | A2 | A3 | A4 |
| -4 | ||||
| 8/3 | ||||
| -4/3 |
38. Какое множество определяет система уравнений:
a. X + Y =3
b. 2X – 3Y =1
c. X + Y – Z =3
d. 2X -3Y =1
Ваша матрица
| № | X1 | X2 | X3 | b |
| -3 | ||||
| -1 | ||||
| -3 |
Нашли единицу в 1-ом столбце в 1-ой строке
| № | X1 | X2 | X3 | b |
| -3 | ||||
| -1 | ||||
| -3 |
Занулили 1-ый столбец
| № | X1 | X2 | X3 | b |
| -5 | -5 | |||
| -1 | ||||
| -5 | -5 |
Получили единицу в 2-ом столбце разделив 2-ую строку на -5
| № | X1 | X2 | X3 | b |
| -1 | ||||
| -5 | -5 |
Занулили 2-ой столбец
| № | X1 | X2 | X3 | b |
| -1 | ||||
Нашли единицу в 3-ем столбце в 3-ей строке (изменив знак на противоположный у всей строки)
| № | X1 | X2 | X3 | b |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|