
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Замена переменной в определенном интеграле
Замена переменной в определенном интеграле
Пусть задан интеграл 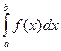 , где f(x) – непрерывная функция на отрезке [a, b].
, где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t). Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то
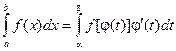
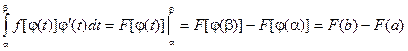
Пример 2. 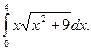
Решение. Выполним замену (аналогично замене переменной в неопределенном интеграле): 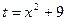 ;
; 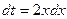 ;
; 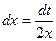 .
.
Введем новые переменные интегрирования. Полагая х = 0 и х = 4, подставим их в замену и получим t = 9 и t = 25. Следовательно,
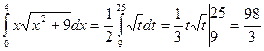
Интегрирование по частям в определенном интеграле
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
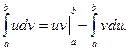
Выбор u и dv осуществляется также как и в неопределенном интеграле.
Пример 3. 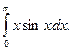
Решение. Выполним замену. Положим 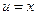 ,
, 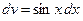 ; тогда
; тогда 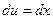 ,
, 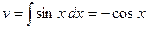 . Подставив в формулу интегрирования по частям, получим
. Подставив в формулу интегрирования по частям, получим
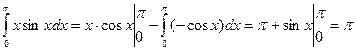 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|