Контакты

Случайная статья

Лекция по электродинамике 20.01.2021

Стр 1 из 2Следующая ⇒

Лекция по электродинамике 20.01.2021

23. Уравнение Максвелла при отсутствии зарядов. Волновое уравнение. Электромагнитные волны

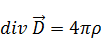
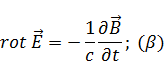
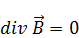
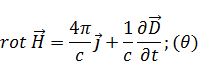
Будем рассматривать электромагнитное поле в отсутствии зарядов и токов.

Это может быть вещество, среда – свободных зарядов и токов нет. Могут быть только связанные заряды и молекулярные токи. Поэтому у нас остается:

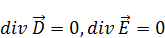
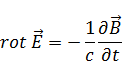
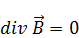Вихревое магнитное поле создается только изменением электрического поля

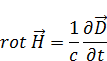
Изотропные означают в любом направлении свойства одинаковые. Какую бы мы систему отсчета не выбрали ничего не поменяется. 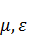- скаляры, не зависят от направления. Однородные – означают, что 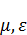– константы.

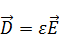
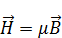
Применим к закону Фарадея ротор:

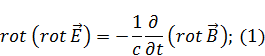
Через вектор набла:

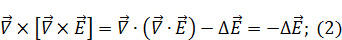
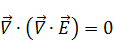, т.к.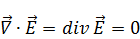

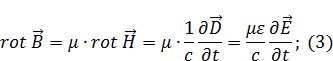
Слева в выражении (1) будет (2), а вместо 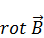в правом выражении для (1) будет выражение (3), тогда:

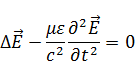
Находим ротор от ротора :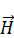

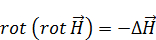
И аналогично выкладкам выше выражение для :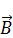

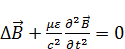– волновое уравнение для .

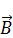Запишем волновое уравнение для скалярного и векторного потенциала:

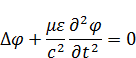
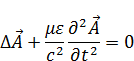
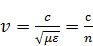– скорость распространения взаимодействия.

Однородная изотропная среда, перепишем уравнения Максвелла:

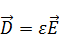
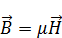
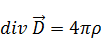
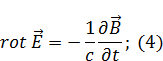
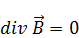
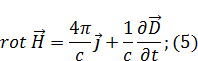
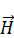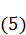Умножим (4) на , а на :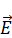

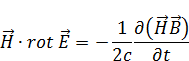
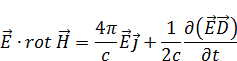
Напишем дивергенцию от векторного произведения 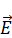и :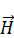

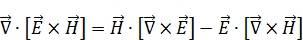
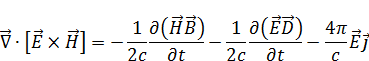
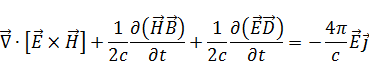
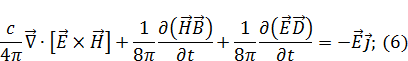
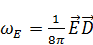– плотность энергии электрического поля

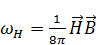– плотность энергии магнитного поля

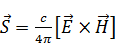– вектор Умова-Пойнтинга.

Используя новые обозначения, перепишем выражение (6):

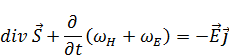
Если токов нет, то:

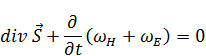
Полученное выражение говорит нам о том, что изменение электрического и магнитного энергий происходит за счет потока .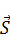

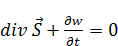– уравнение неразрывности

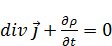– уравнение неразрывности для заряда.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.