Контакты

Случайная статья

Двойные интегралы. Аналитическое вычисление двойного интеграла. Численное определение двойного интеграла. Тройные интегралы.. Дополнительные задания

ЛАБОРАТОРНАЯ РАБОТА № 2.

Применение ЭВМ к решению задач геометрии и механики (двойные и тройные интегралы). Задачи.

Двойные интегралы

Решение в MATLAB:

Аналитическое вычисление двойного интеграла

>> syms x y ;

>> Ix = int(1-x-y, y, 0, 1-x)

>> Ix = int(1-x-y, y, 0, 1-x)

Ix =

1-x-x*(1-x)-1/2*(1-x)^2

>> I = int (Ix, x, 0, 1)

I =

1/6

Численное определение двойного интеграла

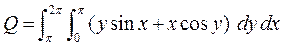
pi <= x <= 2*pi, 0 <= y <= pi:

1)

>> Q = dblquad(@(x,y) y*sin(x)+x*cos(y), pi, 2*pi, 0, pi)

Q =

-9.86960437725457

2) Q = dblquad(@integrnd, pi, 2*pi, 0, pi)

где integrnd - это M-file function:

%-------------------------%

function z = integrnd(x, y)

z = y*sin(x)+x*cos(y);

%-------------------------%

>> Q = dblquad(@integrnd, pi, 2*pi, 0, pi)

Q =

-9.86960437725457

Тройные интегралы.

Решение в MATLAB:

Аналитическое вычисление тройного интеграла

>> syms x y z;

>> Ixy=int(z*x*y,z, 0, 1-x-y)

Ixy =

1/2*x*y*(1-x-y)^2

>> Ix=int(Ixy, y, 0,1-x)

Ix =

3/8*x*(1-x)^4+1/6*x*(-2+2*x)*(1-x)^3

>> I=int (Ix, x, 0,1)

I =

1/720

Численное определение тройного интеграла

Пример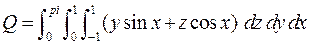

Q = TRIPLEQUAD(@FUN,XMIN,XMAX,YMIN,YMAX,ZMIN,ZMAX,TOL)

1)

>> Q = triplequad(@(x,y,z)(y*sin(x)+z*cos(x)), 0,pi,0,1,-1,1)

Q =

2.0000

>> Q = triplequad(@(x,y,z) (y*sin(x)+z*cos(x)), 0, pi, 0, 1, -1, 1, 0.00000001)

Q =

1.99999999995544

2)

function f = integrnd(x, y, z)

f = y*sin(x)+z*cos(x);

>> Q = triplequad(@integrnd, 0, pi, 0, 1, -1, 1)

Q =

2.0000

1)

2)

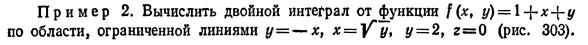
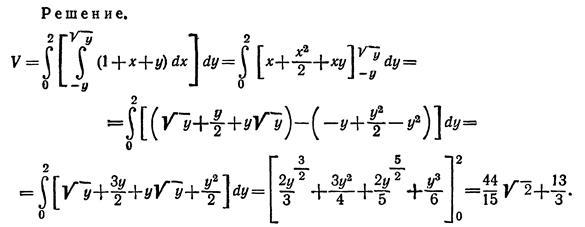
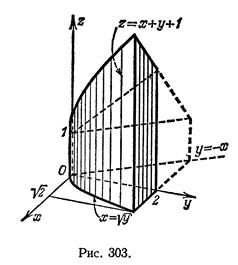
3)

4)

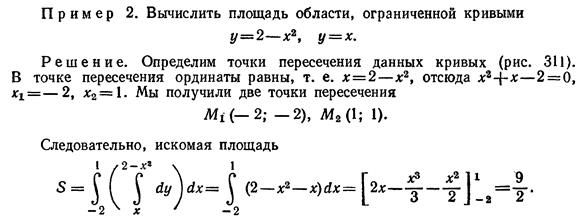
5)

6)

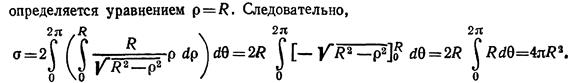
7)

8)

9)

10)

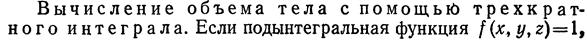
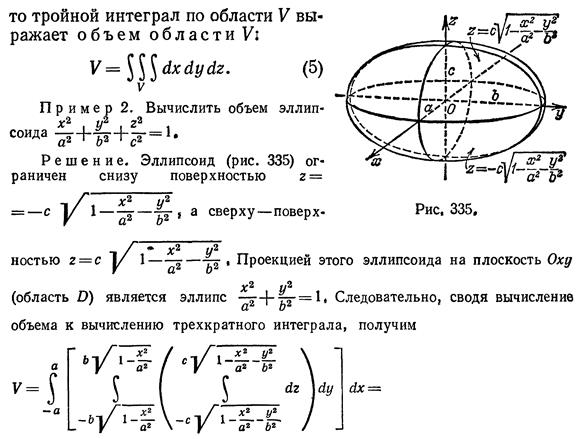
11)

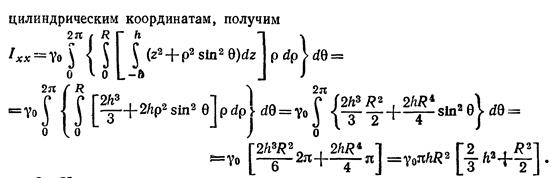
12)

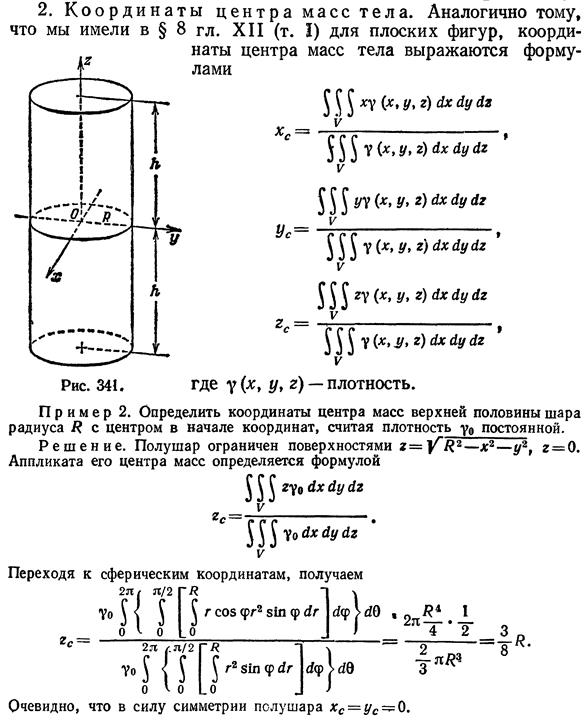
Дополнительные задания

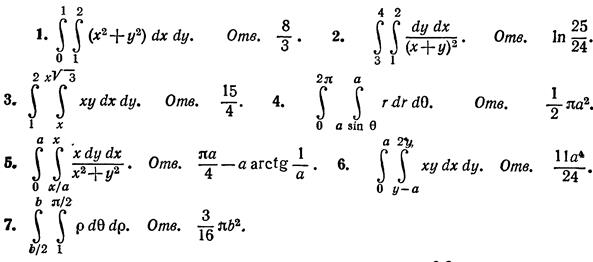
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.