
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лабораторная работа 2.. ИССЛЕДОВАНИЕ СТАТИЧЕСКИХ РЕжимов ДИНАМИЧЕСКОЙ СИСТЕМЫ. Постановка задачи
Лабораторная работа 2.
ИССЛЕДОВАНИЕ СТАТИЧЕСКИХ РЕжимов ДИНАМИЧЕСКОЙ СИСТЕМЫ
Цель работы:преобразовать исходную систему уравнений в СНЛАУ, описывающyю статические режимы; используя пакет MATLAB, решить полученную СНЛАУ и рассчитать статические характеристики динамической системы.
Постановка задачи
Статический режим динамической системы, т.е. системы, представляемой в обычном виде дифференциальными уравнениями – это ее равновесное состояние, соответствующее окончанию переходных процессов.
Статический режим будет описывать система алгебраических уравнений, т. е. уравнений, куда не входят производные, так как последние в статическом режиме равны нулю.
Статическое состояние системы‑ это состояние, при котором переменные состояния (т.е. выходные) остаются без изменения, т.е.:
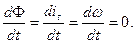
Зависимость от входных управляющих воздействий:
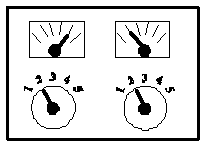

Семейство статич. характеристик зависимости вых. параметров от входных воздействий.
Была дана система уравнений, описывающая динамическую систему:
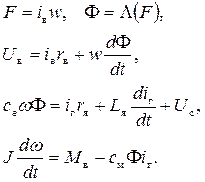
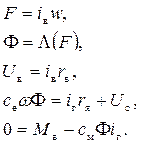
Исключим переменные, которые не являются переменными состояния ( 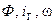 ).
).
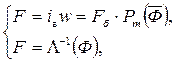
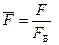 ,
, 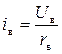
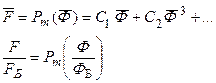
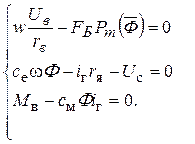
Произведем нормирование всех переменных входа и выхода (все расчеты вести в нормированных величинах), в качестве базовых- номинальные значения.
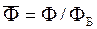 ,
, 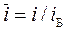 ,
, 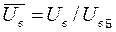 ,
, 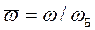
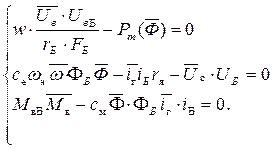
Эту систему легко переписать через переменные 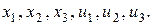
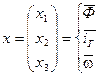
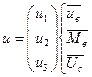 , у кого-то
, у кого-то 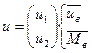 .
.
Приводим уравнение к стандартной форме относительно компонент векторов uи х:
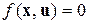
или
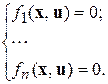
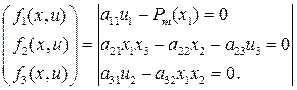
Для каждого набора значений входных воздействий необходимо решить СНЛАУ. Решение, как правило, ищут численным методом, н-р, методом Ньютона для одного и системы уравнений в матричной форме.
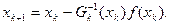
Вычисления продолжают пока
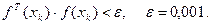
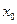 - начальное условие,
- начальное условие, 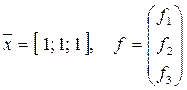
Для реализации метода Ньютона необходимо найти матрицу частных производных:
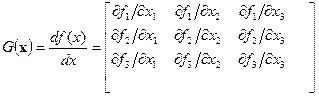 .
.
(кол-во строк=кол-ву f , кол-во столбцов = кол-ву х)
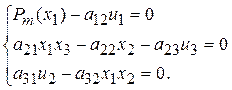
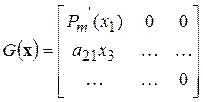 .
.
Т.о. необходимо построить семейство статических характеристик
(3 зависимости от 3-х вх. воздействий, 3 графика на каждую из них).
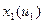
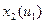
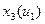
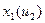
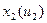
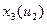
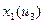
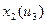
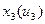
1)
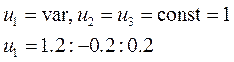
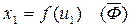
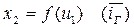
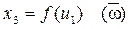
2)
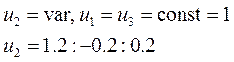
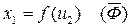
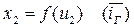
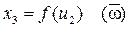
3)
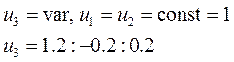
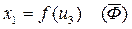
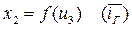
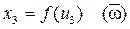
К программе на Matlab
При уменьшении входных управляющих воздействий на 20%
1) 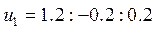
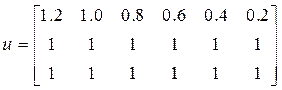
u = [u1; ones(2, length (u1)]
для случая 2)
u = [ones(size(u1)); u1; ones(size(u1))]
Понадобится следующая функция языка МАTLAB, реализующая решение СНЛАУ методом Ньютона:
x=newton(‘fun_F’, ‘fun_G’ , x0, u, eps)
где ‘fun_F’ – имя функции, вычисляющей 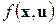 ; ‘fun_G’ – имя функции, вычисляющей матрицу частных производных
; ‘fun_G’ – имя функции, вычисляющей матрицу частных производных 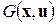 ; x0 – точка начального приближения; u – вектор значений
; x0 – точка начального приближения; u – вектор значений 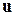 ; eps – точность метода; x – вектор значений решения СНЛАУ. Функция newton не входит в состав пакетов прикладных программ среды MATLAB.
; eps – точность метода; x – вектор значений решения СНЛАУ. Функция newton не входит в состав пакетов прикладных программ среды MATLAB.
Результаты:
1) ф-ции левых частей- fun_F, fun_G (матрица частных производных)
2) plot( 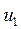 , x(1, :)); выводит график
, x(1, :)); выводит график 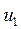 от значений, содержащихся в первой строке матрицы x. Всего 12 графиков для 3-х перем-х.
от значений, содержащихся в первой строке матрицы x. Всего 12 графиков для 3-х перем-х.
3) при номинальных значениях u, значения переменных состояния 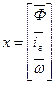 .
.
4) Вывод о характере полученных статических характеристик переменных состояния (описать полученные зависимости).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|