
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛАБОРАТОРНАЯ РАБОТА № 5
ЛАБОРАТОРНАЯ РАБОТА № 5
Основные принципы квантовой информатики
Обозначения Дирака
В квантовой механике действует принцип суперпозиции. Суть которого состоит в следующем: любую волновую функцию можно представить в виде линейной комбинации базисных волновых фукций, т.е. в в виде суммы произведений коэффициента (в обще виде комплексного числа) на соответствующую базисную волновую функцию. Базисные волновые функции должны соответствовать граничным условиям. Каждая базисная функция имеет уникальный набор квантовых чисел, определяющих состояние квантовой системы.
Прежде всего, давайте договоримся записывать скалярное произведение векторов x и y несколько необычным образом: 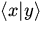 .Более того, давайте формально разделим этот символ на две части:
.Более того, давайте формально разделим этот символ на две части:
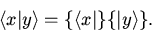
Первая часть этого символа -- 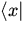 называется бра-вектором, вторая --
называется бра-вектором, вторая -- 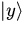 -- кет-вектором. Название происходит от английского слова bracket -- скобки.
-- кет-вектором. Название происходит от английского слова bracket -- скобки.
Может показаться странным, что один и тот же вектор y мы можем по собственному желанию записывать, то как бра-вектор 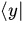 ,то как кет-вектор
,то как кет-вектор 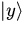 .
.
Чтобы разобраться в этой ситуации, будем отождествлять произвольный вектор y пространства H (пространства волновых функций) с кет-вектором 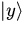 Тогда всякий бра-вектор
Тогда всякий бра-вектор 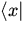 с помощью формулы
с помощью формулы 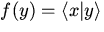 задает линейный непрерывный функционал на пространстве H. Но и обратно всякий непрерывный линейный функционал на H может быть записан в виде скалярного произведения
задает линейный непрерывный функционал на пространстве H. Но и обратно всякий непрерывный линейный функционал на H может быть записан в виде скалярного произведения 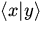 .Следовательно, бра-векторы можно отождествить с непрерывными функционалами на H, т. е. с векторами сопряженного пространства H*.
.Следовательно, бра-векторы можно отождествить с непрерывными функционалами на H, т. е. с векторами сопряженного пространства H*.
Отметим, что средние значения параметра квантовых систем К рассчитывают как интеграл от произведения комплексно сопряженной волновой функции на функционал К и волновой функции.
В обозначениях Дирака такое выражение примет вид <y|K|y˃.
Кубит

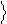

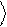 Кубитом называется квантовая система, которая может находиться в двух состояниях 0 и 1 (обозначения Дирака) . Примером такой системы
Кубитом называется квантовая система, которая может находиться в двух состояниях 0 и 1 (обозначения Дирака) . Примером такой системы
может служить фотон с двумя возможными поляризациями или электрон с двумя возможными направлениями спина. В общем случае, состояние такой системы задается волновой функцией вида:

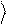

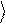 y = a 0
y = a 0
+ b 1
, (1.1)

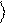

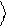



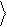 где и b - комплексные коэффициенты. При измерении состояния системы с волновой функцией (1.1), вероятность обнаружить ее в
где и b - комплексные коэффициенты. При измерении состояния системы с волновой функцией (1.1), вероятность обнаружить ее в
 состоянии
состоянии
0 равн
a 2 , а вероятность обнаружить ее в состоянии 1
 равна
равна
b 2 . Сумма этих вероятностей равна единице:



 a 2 + b 2 = 1. (1.2)
a 2 + b 2 = 1. (1.2)
Волновую функцию
y будем рассматривать, как вектор в двумерном

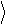


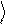 линейном пространстве. При этом волновые функции
линейном пространстве. При этом волновые функции
0 и 1 играют
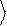

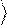
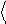


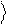 роль базиса этого пространства. Наряду с вектором
роль базиса этого пространства. Наряду с вектором
y , введем

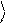 сопряженный вектор
сопряженный вектор
y º y
+ . Тогда скалярное произведение двух

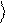

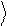

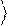 векторов y1
векторов y1
и y2
запишем в виде
y1 y2
. Будем считать основные
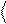

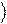 состояния
состояния
0 и 1 ортонормированными:
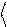

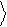
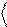

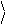 0 0 = 1,
0 0 = 1,
1 1 = 1,
0 1 = 0 . (1.3)

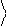
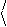

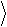
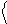 Тогда из условия нормировки волнового вектора кубита вытекает требование (1.2) на коэффициенты a и b .
Тогда из условия нормировки волнового вектора кубита вытекает требование (1.2) на коэффициенты a и b .
y y = 1
сразу
Кубит допускает геометрическое изображение. Рассмотрим сначала случай вещественных коэффициентов a и b .
В этом случае удобно использовать тригонометрическое представление:
a= cos f, b = sin f. (1.4)
Тогда условие (1.2) выполняется автоматически. На плоскости (a,b)
условие (1.2) задает единичную окружность с центром в начале координат
– см. рис.1.
При
f= 0 , в соответствии с (1.4), (1.1) мы получаем
y = 0
, а при
f= p ,

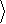

 2
2

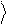

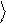 y = 1 .
y = 1 .
 |
Рис.1.Геометрическое изображение кубита
|y˃ = a |0˃ + b|1˃ случай вещественных коэффициентов a и b .
+ b 1
для
представим кубит в виде:

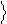
 y = cos J 0
y = cos J 0
+ eif sin J 1
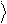

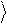 2
2
.(1.5)
Таким образом, полученное представление кубита имеет два параметра -
J и f . Будем интерпретировать их как углы сферической системы координат – см. рис.2.
Кубит представляется вектором единичной длины в трехмерном пространстве. Такое геометрическое изображение кубита называется его

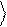

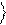

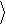 представлением на сфере Блоха. В соответствии с (1.5), при J = 0
представлением на сфере Блоха. В соответствии с (1.5), при J = 0
получаем базисный
0 , а при J = p ,
y = 1
(с точностью до фазового
множителя
eif .

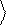

 На сфере Блоха бесконечно много точек. Соответственно, кубит может находиться в одном из бесконечного множества состояний. Казалось бы, используя один кубит, можно хранить бесконечно много информации. Однако, на самом деле это не так. При измерении состояния кубита, он может быть найден в одном из двух возможных состояний - 0 или 1 .
На сфере Блоха бесконечно много точек. Соответственно, кубит может находиться в одном из бесконечного множества состояний. Казалось бы, используя один кубит, можно хранить бесконечно много информации. Однако, на самом деле это не так. При измерении состояния кубита, он может быть найден в одном из двух возможных состояний - 0 или 1 .

 Соответственно, мы можем извлечь из кубита один бит информации. Если бы мы могли получить много одинаковых копий нашего кубита и провести
Соответственно, мы можем извлечь из кубита один бит информации. Если бы мы могли получить много одинаковых копий нашего кубита и провести


 измерение состояния каждой копии, то с вероятностью
измерение состояния каждой копии, то с вероятностью
a 2 мы бы нашли
кубит в состоянии
0 , а с вероятностью
b 2 - в состоянии
1 . Число a 2


 может принимать бесконечно много значений. Таким образом, мы
может принимать бесконечно много значений. Таким образом, мы
получили бы бесконечно много информации, закодированной в одном кубите.
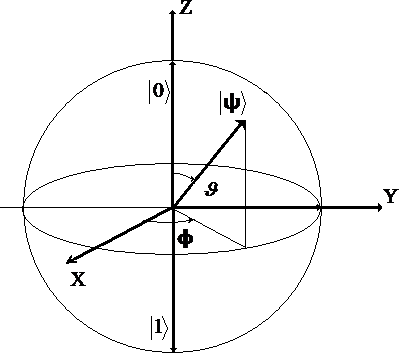 |
Рис.2.Геометрическое изображение кубита
y =a 0
+ b 1
для



 случая комплексных коэффициентов a и b - сфера Блоха.
случая комплексных коэффициентов a и b - сфера Блоха.
Для этого мы должны были бы, в начале, получить сколь угодно копий нашего кубита. Однако существует теорема о невозможности клонирования кубита в неизвестном состоянии, которая будет изложена ниже. Таким образом, из одного кубита можно получить только один бит информации.
Однокубитовые логические элементы

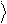 Напомним, что кубит представляет собой квантовую систему, состояние которой задается волновым вектором y (1). Физическое воздействие на
Напомним, что кубит представляет собой квантовую систему, состояние которой задается волновым вектором y (1). Физическое воздействие на

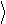 эту систему переводит ее в другое состояние y% :
эту систему переводит ее в другое состояние y% :

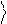

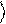 y% = a% 0
y% = a% 0
+ b% 1
. (1.6)

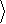 В квантовой механике, любое воздействие на систему описывается линейным оператором Uˆ , действующим на вектор состояния системы:
В квантовой механике, любое воздействие на систему описывается линейным оператором Uˆ , действующим на вектор состояния системы:

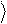

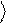 y% = Uˆ y
y% = Uˆ y
. (1.7)

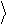 В дальнейшем, воздействие на кубит (или на систему кубитов) мы будем рассматривать, как процесс вычисления. При этом вектор y играет роль
В дальнейшем, воздействие на кубит (или на систему кубитов) мы будем рассматривать, как процесс вычисления. При этом вектор y играет роль

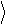 входного сигнала, оператор Uˆ определяет вычислительный процесс, а вектор y% представляет собой результат вычисления – см. рис.3.
входного сигнала, оператор Uˆ определяет вычислительный процесс, а вектор y% представляет собой результат вычисления – см. рис.3.
 |

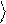

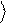 Рис.3.Квантовый логический элемент Uˆ преобразует вектор y в вектор y% .
Рис.3.Квантовый логический элемент Uˆ преобразует вектор y в вектор y% .

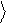 Каждый квантовый вычислительный процесс обратим. То есть, если в результате вычислительного процесса Uˆ входной сигнал | y˃
Каждый квантовый вычислительный процесс обратим. То есть, если в результате вычислительного процесса Uˆ входной сигнал | y˃
был преобразован в выходной сигнал
y% , то существует обратный

 квантовый вычислительный процесс
квантовый вычислительный процесс
Uˆ -1 , который осуществляет обратное
преобразование – см. рис.4. Отметим, что классические вычислительные процессы не всегда обратимы.
 |

 Рис.4.Квантовый логический элемент вектор y .
Рис.4.Квантовый логический элемент вектор y .
Uˆ -1
преобразует вектор
y% в

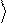 В дальнейшем мы будем использовать матричное представление
В дальнейшем мы будем использовать матричное представление
оператора
Uˆ . Опишем соответствующие конструкции. Рассмотрим
действие оператора на кубит. В силу линейности оператора

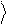

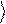 Uˆ y = a% 0
Uˆ y = a% 0
+ b% 1
= Uˆ (a 0
+ b 1 ) = aUˆ
0 + bUˆ
1 . (1.15)

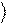

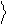

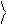

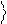

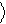

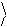

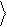 Таким образом, действие оператора на кубит определяется его действием на базисные вектора, 0 и 1 . Эти вектора образуют ортонормированный
Таким образом, действие оператора на кубит определяется его действием на базисные вектора, 0 и 1 . Эти вектора образуют ортонормированный

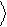

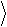

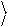 базис в двумерном гильбертовом пространстве. Это значит, что любой вектор этого пространства может быть разложен по базисным векторам.
базис в двумерном гильбертовом пространстве. Это значит, что любой вектор этого пространства может быть разложен по базисным векторам.

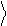 Запишем разложение векторов Uˆ 0
Запишем разложение векторов Uˆ 0
и Uˆ 1
по базису
0 , 1 :

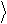

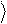 Uˆ 0 = U00 0
Uˆ 0 = U00 0
+ U10 1 ,

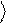

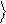 (1.16)
(1.16)

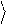

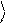 Uˆ 1 = U01 0
Uˆ 1 = U01 0
+ U11 1 .
Согласно (1.16), коэффициенты разложения как
U00 = <0|U|0˃, U10 = <1|U|0˃,
U01 = <0|U|1˃, U11 = <1|U|1˃.
Umn
могут быть рассчитаны
Подставляя (1.16) в (1.15), получаем

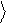 a% 0
a% 0
+ b% 1
= a(U00 0
+ U10 1 ) + b(U01 0
+ U11 1 )

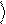

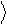

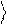

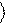

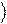 или
или

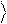

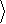 y% = a% 0
y% = a% 0
+ b% 1
= (U00a + U01b) 0

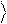

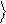 + (U10a + U11 ) 1 .
+ (U10a + U11 ) 1 .

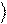

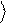 Таким образом, коэффициенты разложения вектора
Таким образом, коэффициенты разложения вектора
y% выражены через

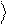 коэффициенты разложения исходного вектора
коэффициенты разложения исходного вектора
y в виде:
a% = U00a + U01b , b% = U10a+ U11b . (1.18)
Введем вектора-столбцы
y = (a,b)
y% = (a%,, , b% )
соответствующие начальному и конечному состояниям кубита и матрицу
|
|
U10
U01 ). (1.19)
Тогда выражение (1.18), связывающее новые и старые компоненты векторов, можно записать в виде:
a%, U00 U01
b% = U10 U11
×
a
b
или
y% = Uy . (1.20)
Матрица называется матричным представлением оператора Uˆ .
00 10
Примеры однокубитовых элементов
2.1. Логический элемент NOT
Обозначим квантовый логический элемент NOT через
Xˆ . Определим

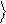

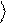

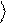

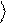 сначала действие этого оператора на базисные вектора. Потребуем, чтобы он переводил 0 в 1 , а 1 в 0 :
сначала действие этого оператора на базисные вектора. Потребуем, чтобы он переводил 0 в 1 , а 1 в 0 :

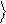

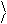 Xˆ 0 = 1 ,
Xˆ 0 = 1 ,
(2.1)

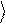

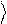 Xˆ 1 = 0 .
Xˆ 1 = 0 .
Тем самым квантовый оператор NOT становится естественным обобщением классического оператора NOT. Используя линейность оператора Xˆ , определим действие оператора на произвольный кубит:

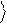

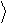 Xˆ y = Xˆ (a 0
Xˆ y = Xˆ (a 0
+ b 1 ) = aXˆ 0
+ bXˆ 1 .

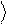

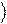

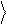 Используя (23), получаем
Используя (23), получаем

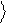

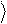 Xˆ y = a 1
Xˆ y = a 1
+ b 0
= b 0
+ a 1
. (2.2)

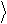

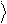

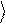

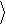

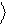 Таким образом, оператор Xˆ векторах 0 и 1 .
Таким образом, оператор Xˆ векторах 0 и 1 .
меняет местами коэффициенты при базисных
Сравнивая (2.1) с (1.16), находим матричные элементы
X00 = 0, X10 = 1, X01 = 1, X11 = 0 .
Xmn
оператора
(2.3)
Xˆ :
Запишем матрицу X оператора
Xmn :
|
Подействуем этой матрицей на вектор входного кубита. Тогда получаем
вектор выходного кубита в виде:
b
a
в соответствии с (2.2).
Действие оператора Xˆ на кубит



 y = a 0 + b 1
y = a 0 + b 1
для вещественных a и b легко интерпретировать геометрически. В вещественном случае используем тригонометрическое представление
a= cos f,
b = sinf,
a% = cos f% ,
b% = sin f% . (2.6)
Тогда, согласно (2.5), (2.6),
f% = π/2 - f
Таким образом, оператор Xˆ поворачивает единичный вектор, изображающий кубит на единичной окружности, отражая его от биссектрисы первого и третьего координатных углов – см. рис.5.
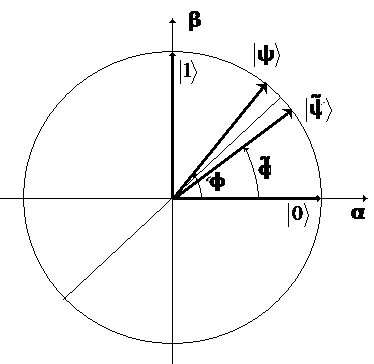 |
Рис.5.Геометрическое изображение преобразования NOT для случая вещественных коэффициентов a иb .
Логический элемент Z

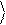

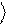

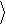 Определим сначала действие оператора Zˆ
Определим сначала действие оператора Zˆ
на базисные вектора.
Потребуем, чтобы он не изменял
0 , а
1 переводил в - 1 :

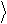

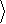 Zˆ 0 = 0 ,
Zˆ 0 = 0 ,
(2.8)

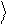

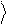 Zˆ 1 =- 1 .
Zˆ 1 =- 1 .
Используя линейность оператора Zˆ , определим действие оператора на произвольный кубит:

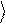

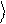 Zˆ y = Zˆ (a 0
Zˆ y = Zˆ (a 0
+ b 1 ) = aZˆ 0
+ bZˆ 1 .

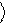

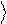

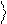 Используя (2.8), получаем:
Используя (2.8), получаем:

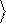

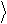 Zˆ y = a 0
Zˆ y = a 0
- b 1
. (2.9)

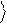 Таким образом, оператор Xˆ
Таким образом, оператор Xˆ
не изменяет коэффициент при базисном

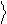

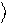 векторе 0 и меняет знак коэффициента при базисном векторе 1 .
векторе 0 и меняет знак коэффициента при базисном векторе 1 .
Сравнивая (2.8) с (1.16), находим матричные элементы
Z00 = 1, Z10 = 0 ,
Zmn
оператора
Zˆ :
Z01 = 0, Z11 = -1.
Запишем матрицу Z оператора
(2.10)
| |
|
Подействуем этой матрицей на вектор входного кубита. Тогда получаем вектор выходного кубита в виде:
a
- b
в соответствии с (2.9).
Действие оператора Zˆ
на кубит:

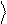

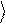

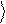 y = a 0 + b 1
y = a 0 + b 1
для вещественных a и b легко интерпретировать геометрически. В вещественном случае используем тригонометрическое представление
a= cos f,
b = sinf,
a% = cos f% ,
b% = sin f% . (2.13)
В самом деле, согласно (2.6), (2.7),
f% = -f. (2.14)
Таким образом, оператор Zˆ
поворачивает единичный вектор,
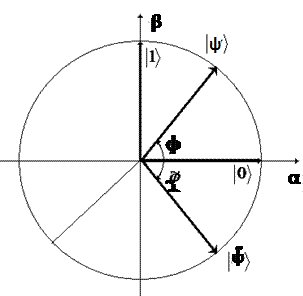 |
изображающий кубит на единичной окружности, отражая его от оси абсцисс – см. рис.6.
Рис.6.Геометрическое изображение преобразования Zˆ
вещественных коэффициентов a и b .
для случая
ЗАДАНИЕ
1. Каким будет выходной кубит, если провести последовательно воздействия на исходный кубит операторов Zˆ и NOT ?
2. Каков будет результат, если провести воздействия этих операторов в обратном порядке? Обоснуйте ответ.
3. Представьте исходный и выходной кубит графически для случая вещественных коэффициентов.
4. Могут ли быть операторы, матрицы которых состоят из одних единиц или одних нулей? Обоснуйте ответ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|