
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица 1
Лабораторная работа №2
РМС 2. ИССЛЕДОВАНИЕ ЗАКОНА МАЛЮСА И ПРОХОЖДЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА ЧЕРЕЗ ФАЗОВУЮ ПЛАСТИНКУ.
Цель работы – Проверка закона Малюса и анализ поляризованного света, прошедшего через фазовую пластинку.
Общие положения.
Из электромагнитной теории света следует, что световая волна является поперечной, то есть три вектора: напряженность электрического поля  , напряженность магнитного поля
, напряженность магнитного поля 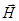 и волновой вектор
и волновой вектор  взаимно перпендикулярны. Свет от обычных источников состоит из множества цугов волн, световой вектор
взаимно перпендикулярны. Свет от обычных источников состоит из множества цугов волн, световой вектор  которых ориентирован в поперечной плоскости случайным образом, а колебания различных направлений равновероятны. Такой свет называется естественным или неполяризованным.
которых ориентирован в поперечной плоскости случайным образом, а колебания различных направлений равновероятны. Такой свет называется естественным или неполяризованным.
Свет, в котором направления колебаний светового вектора упорядочены каким-либо образом, называется поляризованным. Процесс получения поляризованного света называется поляризацией. Если колебания вектора  происходят в одной плоскости, то свет считается плоскополяризованным (или линейно поляризованным). Свет, в котором имеется преимущественное направление колебаний вектора
происходят в одной плоскости, то свет считается плоскополяризованным (или линейно поляризованным). Свет, в котором имеется преимущественное направление колебаний вектора  , называют частично поляризованным.
, называют частично поляризованным.
Плоскость, в которой лежит вектор напряженности электрического поля волны и волновой вектор  , называют плоскостью колебаний или плоскостью поляризации.
, называют плоскостью колебаний или плоскостью поляризации.
Поляризация света наблюдается при отражении, преломлении и при прохождении света через анизотропные вещества. Всякий прибор, служащий для получения поляризованного света (независимо от физических эффектов, используемых при этом), называется поляризатором. Визуально поляризованный свет нельзя отличить от неполяризованного. Исследование поляризованного света осуществляют с помощью того же прибора, называемого в этом случае анализатором.
Эллиптическая поляризация света
Поляризованное излучение имеет в общем случае эллиптическую поляризацию. При этом ортогональные компоненты светового вектора  для выбранной системы координат (ось Z параллельна направлению распространения света) описываются выражениями вида:
для выбранной системы координат (ось Z параллельна направлению распространения света) описываются выражениями вида:
 , (1)
, (1)
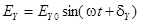 . (2)
. (2)
Сложение ортогональных колебаний вида (1) и (2) на плоскости XY дает проекционную картину эллипса. При этом форма эллипса определяется параметрами:
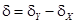 – разность фаз, (3)
– разность фаз, (3)
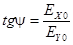 – отношение амплитуд. (4)
– отношение амплитуд. (4)
При δ, равной нулю или π, эллипс вырождается в прямую и получается линейно поляризованный свет. При δ = π/2 и равенстве амплитуд складываемых волн эллипс превращается в окружность – получается свет, поляризованный по кругу.
В зависимости от направления вращения вектора  различают правую и левую эллиптическую поляризацию. Если по отношению к направлению луча вектор
различают правую и левую эллиптическую поляризацию. Если по отношению к направлению луча вектор  вращается по правилу правого винта, поляризация называется правой, в противном случае – левой.
вращается по правилу правого винта, поляризация называется правой, в противном случае – левой.
|
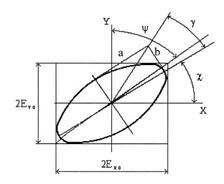
| Рис.1. |
Для описания формы эллипса часто используют другую пару параметров, имеющих более наглядную геометрическую интерпретацию (рис.1):
χ – азимут ориентации большой полуоси эллипса в выбранной системе координат;
tg g = b/a – эллиптичность – отношение полуосей эллипса.
Связь между параметрами задается формулами:
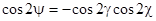 , (5)
, (5)
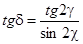 , (6)
, (6)
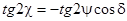 , (7)
, (7)
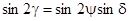 . (8)
. (8)
Представление эллипса поляризации двумя парами параметров и соотношение между ними имеют важное практическое значение. Непосредственно измеряемыми параметрами в большинстве измерительных схем являются величины χ и γ, для физической интерпретации результатов измерений часто более удобны параметры ψ и δ (например, при построении математической модели объекта с использованием законов и формул Френеля для обработки результатов измерений).
 Закон Малюса
Закон Малюса
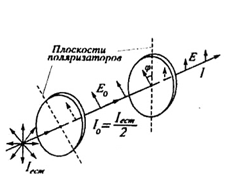
Пусть свет на своем пути проходит через поляризатор и анализатор, причем угол между их плоскостями поляризации составляет φ (рис. 2). После поляризатора выйдет свет, интенсивностью I0. Согласно закону Малюса после анализатора мы получим свет, интенсивность которого определяется выражением
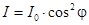 .
.
В справедливости этого выражения нетрудно убедиться, вспомнив, что интенсивность пропорциональна квадрату амплитуды Е.
Если частично поляризованный свет пропускать через анализатор интенсивность I прошедшего света будет меняться в зависимости от положения плоскости поляризации анализатора. Она достигает максимального значения, если плоскость поляризации анализатора и плоскость преимущественных колебаний частично поляризованного света совпадают. Если же эти плоскости перпендикулярны друг другу, то интенсивность света, прошедшего через анализатор, будет минимальной.
Прохождение плоскополяризованного света через кристаллическую пластинку
 При прохождении света через прозрачные кристаллы может наблюдаться явление двойного лучепреломления, заключающееся в том, что упавший на кристалл луч разделяется внутри кристалла на два луча – обыкновенный и необыкновенный. Исследования показывают, что помимо прочих различий эти лучи полностью поляризованы во взаимно перпендикулярных направлениях, связанных с собственными осями кристалла. Оптической осью кристалла называют некоторое выделенное направление, относительно которого свойства кристалла обладают симметрией.
При прохождении света через прозрачные кристаллы может наблюдаться явление двойного лучепреломления, заключающееся в том, что упавший на кристалл луч разделяется внутри кристалла на два луча – обыкновенный и необыкновенный. Исследования показывают, что помимо прочих различий эти лучи полностью поляризованы во взаимно перпендикулярных направлениях, связанных с собственными осями кристалла. Оптической осью кристалла называют некоторое выделенное направление, относительно которого свойства кристалла обладают симметрией.
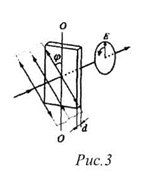
Рассмотрим кристаллическую пластинку, вырезанную вдоль оптической оси. При падении на такую пластинку линейно поляризованного света обыкновенный и необыкновенный лучи распространяются по одной траектории, но приобретают разность фаз, обусловленную различными значениями показателей преломления для обыкновенного и необыкновенного луча. Если толщина пластинки такова, что при прохождении через нее лучи приобретут оптическую разность хода 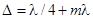 (m = 0, 1, 2...), то разность фаз для них составит π/2. При δ = π/2 и равенстве амплитуд электрических колебаний в обоих лучах поляризация света станет круговой (циркулярной). Такая пластинка называется пластинкой в четверть волны (рис. 3).
(m = 0, 1, 2...), то разность фаз для них составит π/2. При δ = π/2 и равенстве амплитуд электрических колебаний в обоих лучах поляризация света станет круговой (циркулярной). Такая пластинка называется пластинкой в четверть волны (рис. 3).
Пластинка, для которой 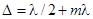 , называется пластинкой в полволны. Она вносит разность фаз, равную π, и прошедший свет в этом случае оказывается линейно поляризованным, но уже в плоскости, отличной от исходной.
, называется пластинкой в полволны. Она вносит разность фаз, равную π, и прошедший свет в этом случае оказывается линейно поляризованным, но уже в плоскости, отличной от исходной.
Описание лабораторной установки
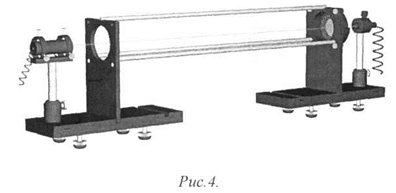
Схема установки приведена на рис. 4. В первой части работы (при исследовании закона Малюса) установка включает в себя полупроводниковый лазер, анализатор и фотоприемник.
 В работе используется лазер, на выходной диафрагме которого установлен дихроичный пленочный поляризатор и, таким образом, выходное излучение является линейно поляризованным, его интенсивность соответствует обозначению I0 в формуле для закона Малюса. Угол изменяется вращением анализатора. Свет, прошедший через анализатор интенсивностью I попадает на фотоприемник (фотодиод), подключенный к
В работе используется лазер, на выходной диафрагме которого установлен дихроичный пленочный поляризатор и, таким образом, выходное излучение является линейно поляризованным, его интенсивность соответствует обозначению I0 в формуле для закона Малюса. Угол изменяется вращением анализатора. Свет, прошедший через анализатор интенсивностью I попадает на фотоприемник (фотодиод), подключенный к
мультиметру. Показания мультиметра пропорциональны световому потоку, попадающему на фотодиод.
Показания с мультиметра следует снимать в режиме измерения тока, так как получаемая в этом случае характеристика является линейной.
Во второй части работы между лазером и анализатором помещается фазовая пластинка из слюды.
На рисунке приведен внешний вид лабораторной установки РМС 1.
Порядок выполнения работы
I. Исследование закона Малюса
Порядок выполнения работы:
1. Установить мультиметр в режим измерения тока I, мА и вращением анализатора установить положение максимального пропускания. Выставить на мультиметре необходимый предел измерений, при котором отсутствует индикация перегрузки.
2. Перекрыть луч лазера оптически непрозрачным материалом и снять отсчет темнового тока фотоприемника IT. Установить анализатор в положение, соответствующее 0°. Снять показания мультиметра в режиме измерения тока I, мА. Затем, поворачивая анализатор через 10° заполнить табл.1 для I.
Таблица 1
| угол | ….. | ||||||||
| I, мА | |||||||||
| I-IT |
Замечание: При выполнении опыта во второй раз необходимо точнее выставлять угол поворота в 10°.
3. Произвести указанные измерения дважды (или большее число раз по заданию преподавателя) и рассчитать средние значения I по результатам изменений.
4. Построить графики зависимостей  и
и 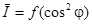 .
.
5. Объяснить полученные результаты.ъ
II. Работа с фазовой пластинкой
1. Вращением установить анализатор в такое положение, чтобы полностью погасить свет, попадающий на фотоприемник.
2. Поместить перед анализатором фазовую пластинку.
3. Вращая пластинку вокруг своей оси, убедиться в наличии таких четырех ее положений, в которых опять будет наблюдаться полное гашение света. Эти положения соответствуют ориентации одной из собственных осей пластинки перпендикулярно плоскости главного пропускания анализатора.
4. Выбрав любое из таких положений, повернуть пластинку на 45° и закрепить ее в этом положении. В указанном случае мы получаем, что плоскость поляризации падающего излучения ориентирована под углом 45° к собственным осям пластинки, и, таким образом, амплитуды обыкновенного и необыкновенного лучей одинаковы.
5. Вращая анализатор, снять показания с мультиметра аналогично первой части работы и заполнить таблицу 1.
6. Построить график зависимости I = f(φ).
7. Найти средние значения Imin и Imах.
8. Рассчитать эллиптичность, равную отношению малой и большой полуосей эллипса, выраженную следующим образом
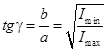 .
.
9. При выполнении условия ориентации осей фазовой пластинки под углом 45° к плоскости поляризации падающего света (п. 4) разность фаз связаны между собой простым соотношением: δ = 2γ. Данная формула следует из выражений (6), (8) а также иллюстрируется следующими примерами: при разности фаз между обыкновенным и необыкновенным лучом δ = 0 или δ = π, как было описано выше, эллипс вырождается в прямую – эллиптичность обращается в ноль или бесконечность, при tg(π/4) или tg(3π/4) эллипс превращается в круг.
10. При известной толщине пластинки из слюды можно рассчитать разность показателей преломления обыкновенного и необыкновенного лучей (no – nе).
Контрольные вопросы:
1. Естественный и поляризованный свет. Прохождение света через поляризатор и анализатор.
Закон Малюса.
2. Поляризация при отражении и преломлении от диэлектриков. Закон Брюстера.
3. Двойное лучепреломление. Поляризация при двойном лучепреломлении. Призма Николя и поляроидные пленки.
4. Оптическая активность. Вращение плоскости поляризации
5. Поляризационные устройства. Пластинки «λ/4» и «λ/2». Интерференция поляризованных волн
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|