
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Элементы линейной алгебры. Введение в математический анализ
Задача 1.Даны векторы 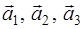 и
и 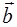 в некотором базисе трехмерного пространства. Показать, что векторы
в некотором базисе трехмерного пространства. Показать, что векторы 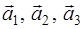 образуют базис данного трехмерного пространства и найти координаты вектора
образуют базис данного трехмерного пространства и найти координаты вектора 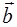 в этом базисе.
в этом базисе.
1.1. 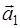 (1;2;3),
(1;2;3), 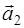 (-1;3;2),
(-1;3;2), 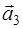 (7;-3;5),
(7;-3;5), 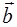 (6;10;17).
(6;10;17).
1.2. 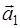 (4;7;8),
(4;7;8), 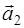 (9;1;3),
(9;1;3), 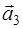 (2;-4;1),
(2;-4;1), 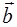 (1;-13;-13).
(1;-13;-13).
1.3. 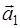 (8;2;3),
(8;2;3), 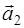 (4;6;10),
(4;6;10), 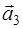 (3;-2;1),
(3;-2;1), 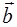 (7;4;11).
(7;4;11).
1.4. 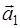 (10;3;1),
(10;3;1), 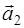 (1;4;2),
(1;4;2), 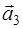 (3;9;2),
(3;9;2), 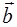 (19;30;7).
(19;30;7).
1.5. 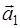 (2;4;1),
(2;4;1), 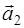 (1;3;6),
(1;3;6), 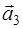 (5;3;1),
(5;3;1), 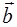 (24;20;6).
(24;20;6).
1.6. 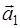 (1;7;3),
(1;7;3), 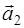 (3;4;2),
(3;4;2), 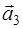 (4;8;5),
(4;8;5), 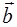 (7;32;14).
(7;32;14).
1.7. 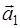 (1;-2;3),
(1;-2;3), 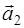 (4;7;2),
(4;7;2), 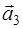 (6;4;2),
(6;4;2), 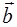 (14;18;6).
(14;18;6).
1.8. 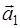 (1;4;3),
(1;4;3), 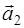 (6;8;5),
(6;8;5), 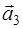 (3;1;4),
(3;1;4), 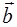 (21;18;33).
(21;18;33).
1.9. 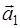 (2;7;3),
(2;7;3), 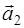 (3;1;8),
(3;1;8), 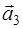 (2;-7;4),
(2;-7;4), 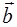 (16;14;27).
(16;14;27).
1.10. 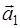 (7;2;1),
(7;2;1), 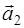 (4;3;5),
(4;3;5), 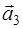 (3;4;-2),
(3;4;-2), 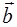 (2;-5;-13).
(2;-5;-13).
Задача 3. Даны вершины 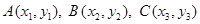 треугольника. Найти: 1) длину стороны
треугольника. Найти: 1) длину стороны 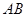 ; 2) внутренний угол
; 2) внутренний угол 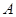 в радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину
в радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину 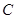 ; 4) уравнение медианы, проведенной через вершину
; 4) уравнение медианы, проведенной через вершину 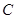 ; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины
; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины 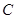 ; 7) систему неравенств, определяющих треугольник
; 7) систему неравенств, определяющих треугольник 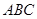 . Сделать чертеж.
. Сделать чертеж.
3.1. 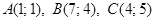 .
.
3.2. 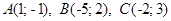 .
.
3.3. 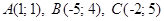 .
.
4.4. 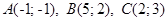 .
.
3.5. 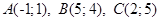 .
.
3.6. 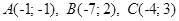 .
.
3.7. 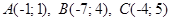 .
.
3.8. 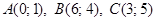 .
.
3.9. 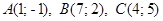 .
.
3.10. 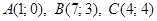 .
.
Задача 4.Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4;  3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
4.1. А1(4;2;5), А2(0;7;2), А3(0;2;7), А4(1;5;0).
4.2. А1(4;4;10), А2(4;10;2), А3(2;8;4), А4(9;6;4).
4.3. А1(4;6;5), А2(6;9;4), А3(2;10;10), А4(7;5;9).
4.4. А1(3;5;4), А2(8;7;4), А3(5;10;4), А4(4;7;8).
4.5. А1(10;6;6), А2(-2;8;2), А3(6;8;9), А4(7;10;3).
4.6. А1(1;8;2), А2(5;2;6), А3(5;7;4), А4(4;10;9).
4.7. А1(6;6;5), А2(4;9;5), А3(4;6;11), А4(6;9;3).
4.8. А1(7;2;2), А2(5;7;7), А3(5;3;1), А4(2;3;7).
4.9. А1(8;6;4), А2(10;5;5), А3(5;6;8), А4(8;10;7).
4.10. А1(7;7;3), А2(6;5;8), А3(3;5;8), А4(8;4;1).
Элементы линейной алгебры
Задача 6. Дана система линейных уравнений

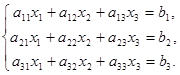
Доказать ее совместность и решить двумя способами: 1) методом Крамера; 2) средствами матричного исчисления:
6.1. 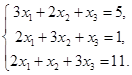
6.2. 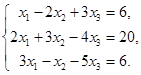
6.3. 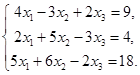
6.4. 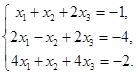
6.5. 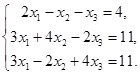
6.6. 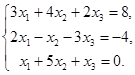
6.7. 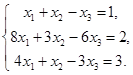
6.8. 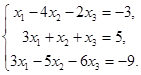
6.9. 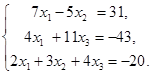
6.10. 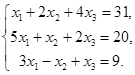
Введение в математический анализ
Задача 7.Найти пределы функций, не пользуясь правилом Лопиталя:
7.1.
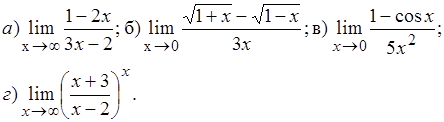
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|