Контакты

Случайная статья

КИНЕМАТИКА. Основные формулы

. КИНЕМАТИКА

Основные формулы

Средняя скорость тела за промежуток времени Δt определяется отношением перемещения тела Δrк промежутку времени Δt:

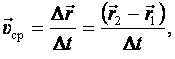
где – радиус–вектор начальной точки, 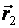– конечной.

Средний модуль скорости тела за промежуток времени Δt есть отношение пути S, пройденного телом за это время, к Δt:

.

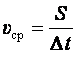Средним ускорением называется отношение изменения скорости ко времени, за которое оно произошло:

.

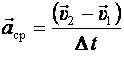Мгновенная скорость 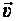равна производной радиус-вектора точки по времени

и направлена по касательной к траектории; для прямолинейного движения ,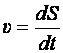

ускорения .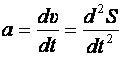

Кинематические соотношения для прямолинейного равнопеременного движения:

,

,

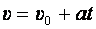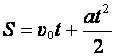где υ₀ скорость тела в момент времени t = 0, a – ускорение тела.

При криволинейном движении полное ускорение тела раскладывается на нормальную и тангенциальную к траектории составляющие: .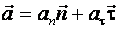

Тангенциальная составляющая ускорения определяет изменение модуля скорости: ,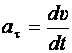

нормальная – изменение направления скорости:

,

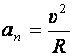где R–радиус кривизны траектории, нормальное ускорение направлено к центру кривизны траектории.

Модуль полного ускорения:

.

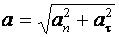При движении по окружности кинематическими характеристиками являются:

– угол поворота φ,

– угловая скорость ω = ,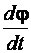

– угловое ускорение ε= = .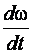

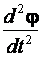Кинематические уравнения для вращательного равнопеременного движения:

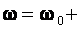ε t

φ = ω₀t + ε,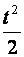

где ω₀– угловая скорость в момент времени t=0, e – угловое ускорение.

Линейные и угловые параметры движения связаны соотношением: υ = ω R, a_τ = εR.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.