Хелпикс

Главная

Контакты

Случайная статья



Кинематика



Кинематика

Задача К22

 

Диск радиусом R вращается вокруг своего неподвижного вертикального диаметра с угловой скоростью ω. По ободу этого диска перемещается точка М так, что угол О1ОМ= φ = f(t). Определить абсолютную скорость и абсолютное ускорение точки М в момент t1 (рис. 52, табл. 61, где φ – в рад, R – в см , t1- сек, ω - в с-2).

 

 

 

 

Рис. 52

 

  Таблица 61

 

№
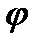
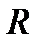
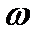
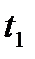
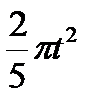
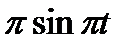
2.5
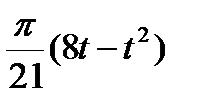
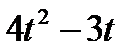
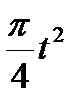
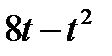
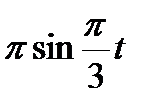
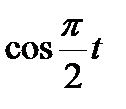
2.5
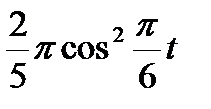
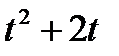
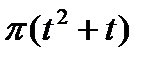
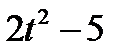
3.5
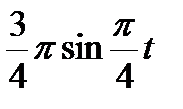
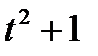
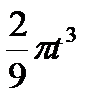
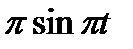
1.5

 

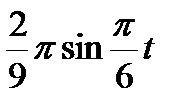
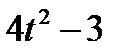
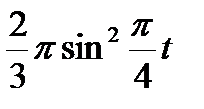
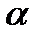Задача К23.

Прямоугольный треугольник ABC с гипотенузой BC=a и углом α вращается вокруг катета AC с угловой скоростью ω. По его гипотенузе перемещается точка М по закону СМ= s = f(t). Определить абсолютную скорость и абсолютное ускорение точки М в момент t1 (рис. 53, табл. 62, длины заданы в см, t1- сек, ω - в с-1).

 

   

 

 

   Рис. 53

 

  

 

 

Таблица 62

 

№
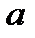
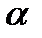
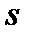
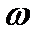
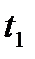
60°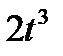
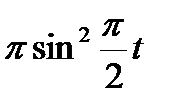
45°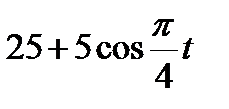
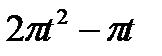
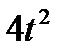
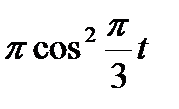
60° 2.5
30°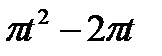
45°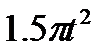
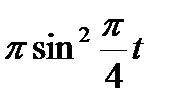
45°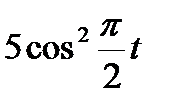
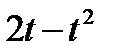
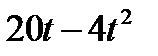
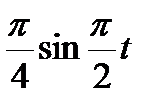
45° 2.5
30° 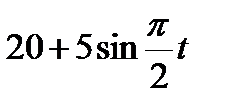1.5
30°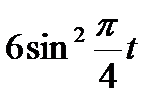
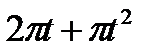
60°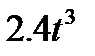

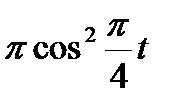
Задача К24.

 

В кулисном механизме при качании кривошипа ОС вокруг неподвижной оси О, перпендикулярной к плоскости чертежа, ползун А, перемещаясь вдоль кривошипа ОС, приводит в движение стержень АВ, соединенный с ползуном А шарнирно и перемещающийся в наклонных направляющих, образующих с осью Ох угол 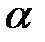. Определить скорость и ускорение стержня АВ в момент t1, если заданы угол поворота кривошипа φ, отсчитываемый от положительного направления оси Ох как функция времени t, и расстояние h (рис. 54, табл. 63, где h — в см, φ — в рад).

 

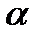 Рис. 54

 

     

 

 

 Таблица 63

№
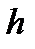
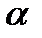
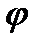
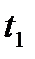
0°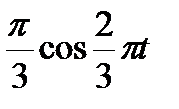
60°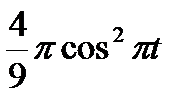
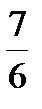
90°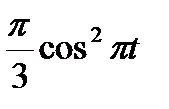
45°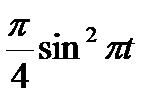
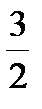
45°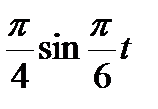
60°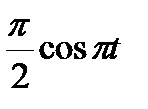
30°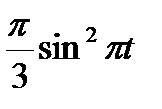
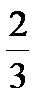
90°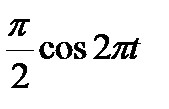
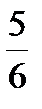
0° 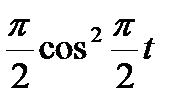1.5
90° 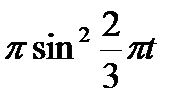3.5

 

 

Задача К25.

 

 Кран вращается вокруг вертикальной оси по закону φ= f1(t). Крановая тележка перемещается по закону s = f2 (t). Определить абсолютную скорость и абсолютное ускорение тележки в момент t1 (рис. 60, табл. 64, где φ — в рад, a t — в сек).

                                                 

 

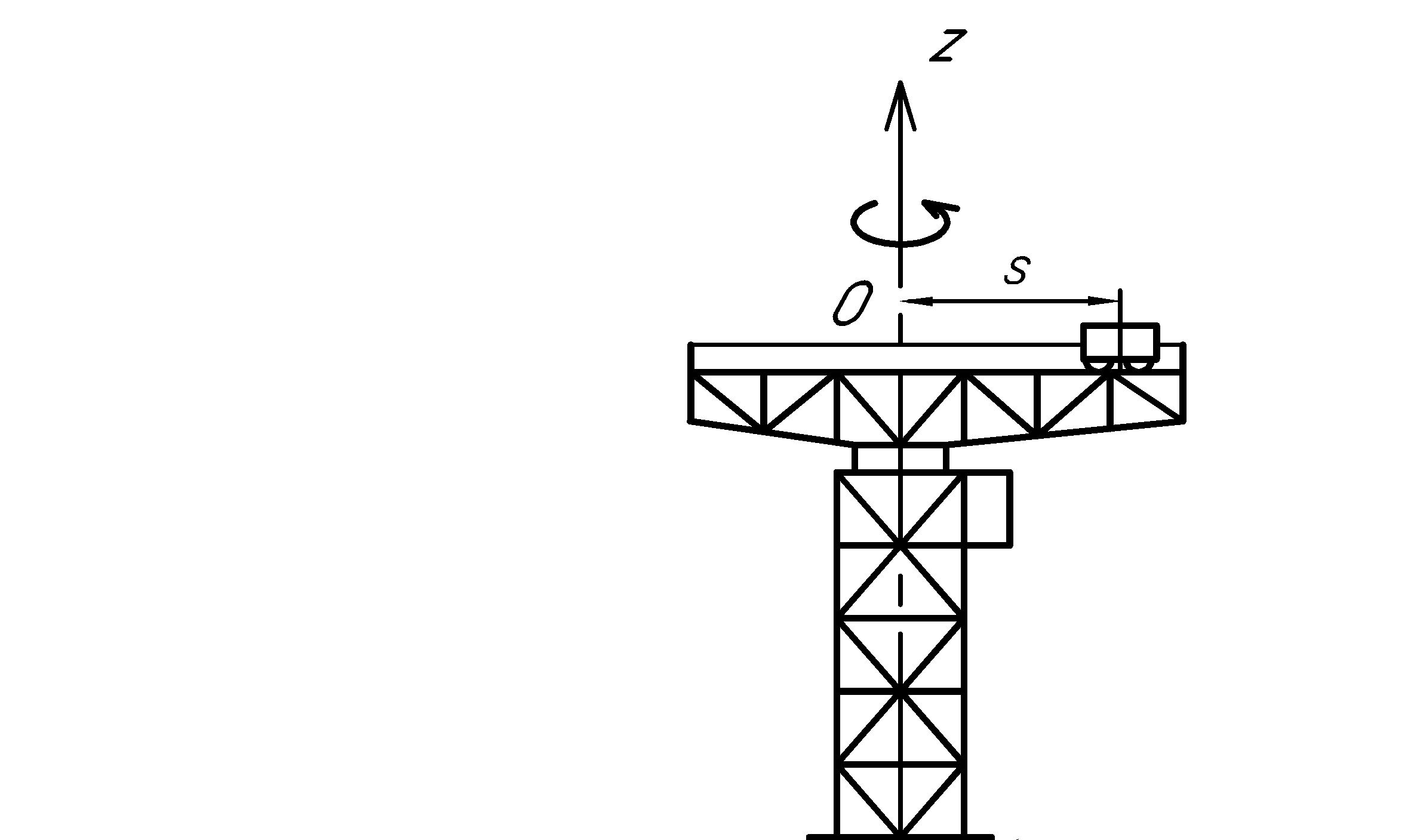
Таблица 64

 

№

 

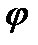
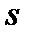
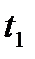
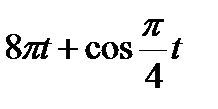
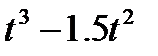
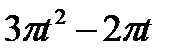
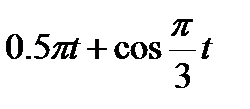
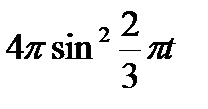
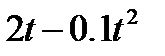
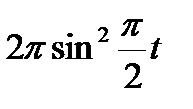
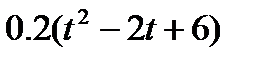
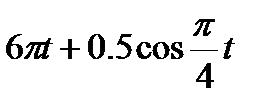
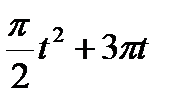
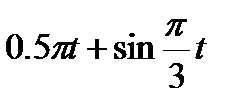
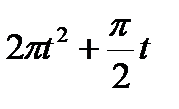
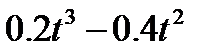
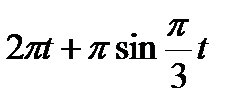
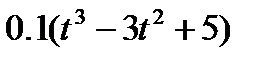
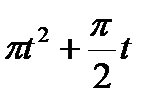
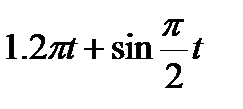
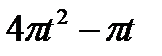
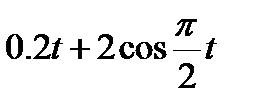
Задача К26.

 

Прямоугольник ABCD вращается вокруг оси Oz по закону φ= f1(t). По его диагонали АС перемещается точка М по закону AM=s = f2(t). Определить абсолютную скорость и абсолютное ускорение точки М в момент t1 сек, если диагональ АС составляет с осью вращения угол 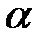 (рис. 61, табл. 65, где s – в см, а угол φ- в рад).

 

 

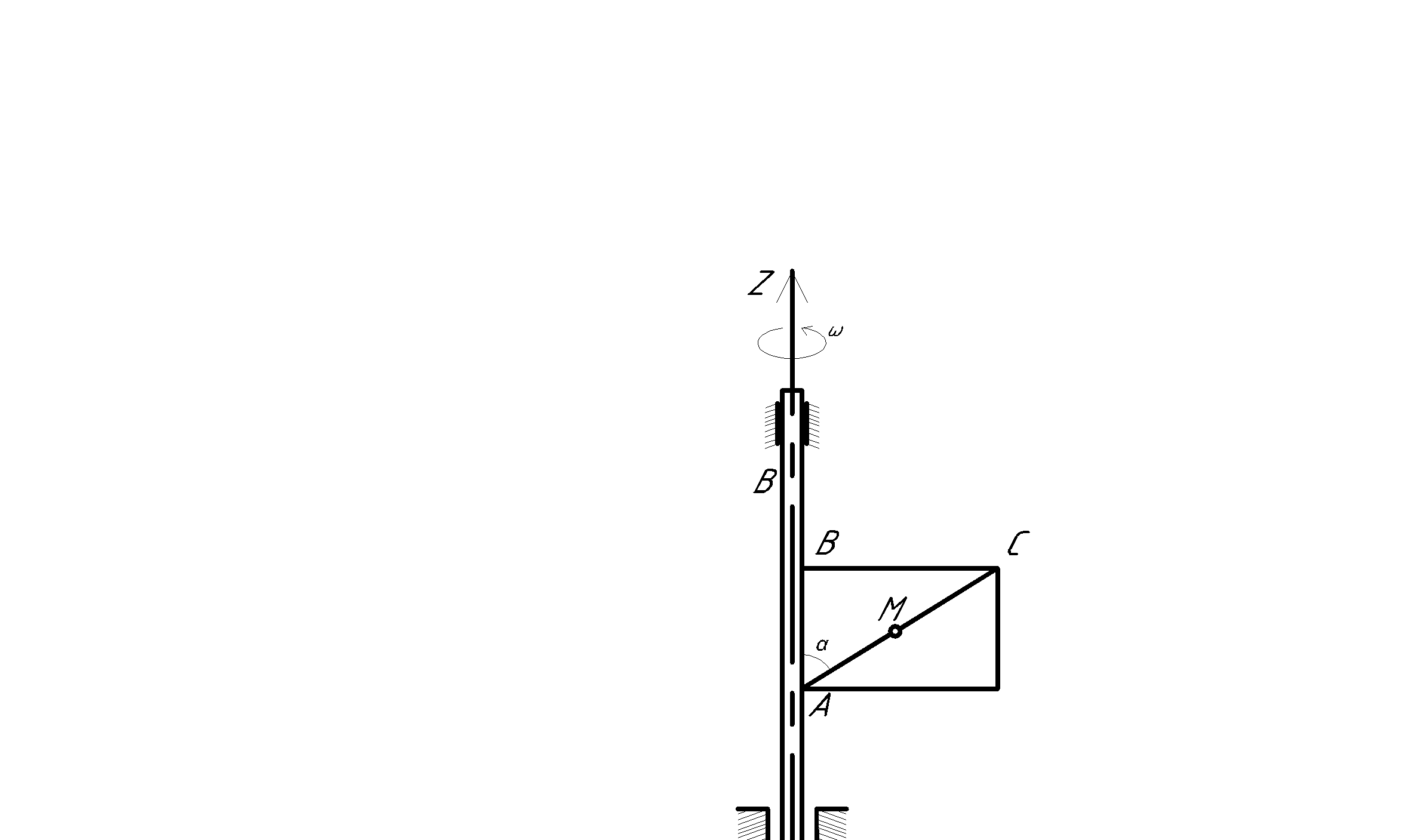
  Таблица 65

 

№
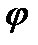
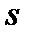
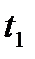
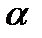
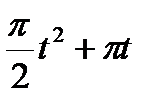
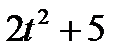
45°
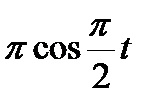
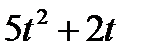
30°
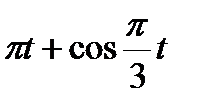
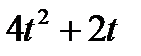
30°
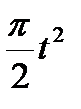
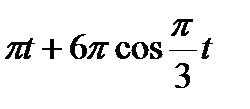
60°
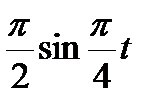
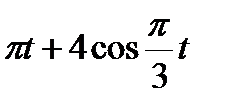
45°
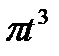
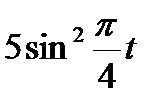
60°
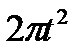
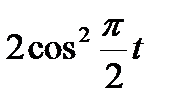
30°
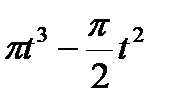
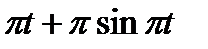
45°
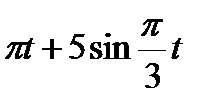
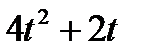
60°
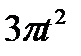
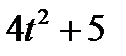
1.5 45°

 

Задача К27.

 

Диск вращается вокруг своего горизонтального диаметра с угловой скоростью ω. По его диаметру, наклоненному к оси вращения под углом 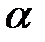, перемещается точка М по закону OM = s=f (t). Определить абсолютную скорость и абсолютное ускорение точки М в момент t1 (рис. 57, табл. 66, где s — в см, ω — в с-1, t — в сек).

 

 

Рис. 57

      

Таблица 66

№
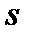
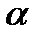
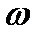
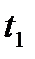
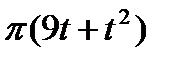
45°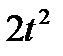
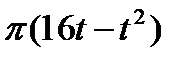
60°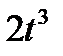
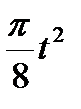
30°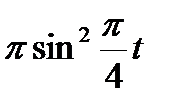
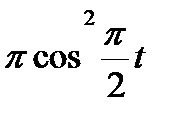
45° 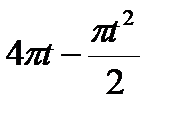2.5
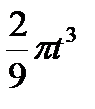
30°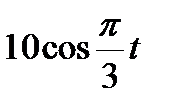
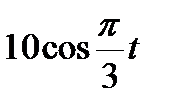
90° 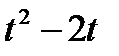0.75
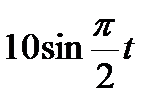
45° 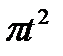0.5
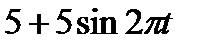
90° 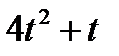0.75
60°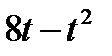
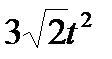
30°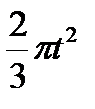

 

Задача К28.

 

Точка М движется по образующей конуса по закону s = OM=f1(t). Конус вращается вокруг своей оси с угловой скоростью ω = f2(t). Определить абсолютную скорость и абсолютное ускорение точки М в момент t1, если угол МОА = 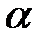 (рис. 63, табл. 67; s задано в см, t — в сек, ω — в с-1).

 

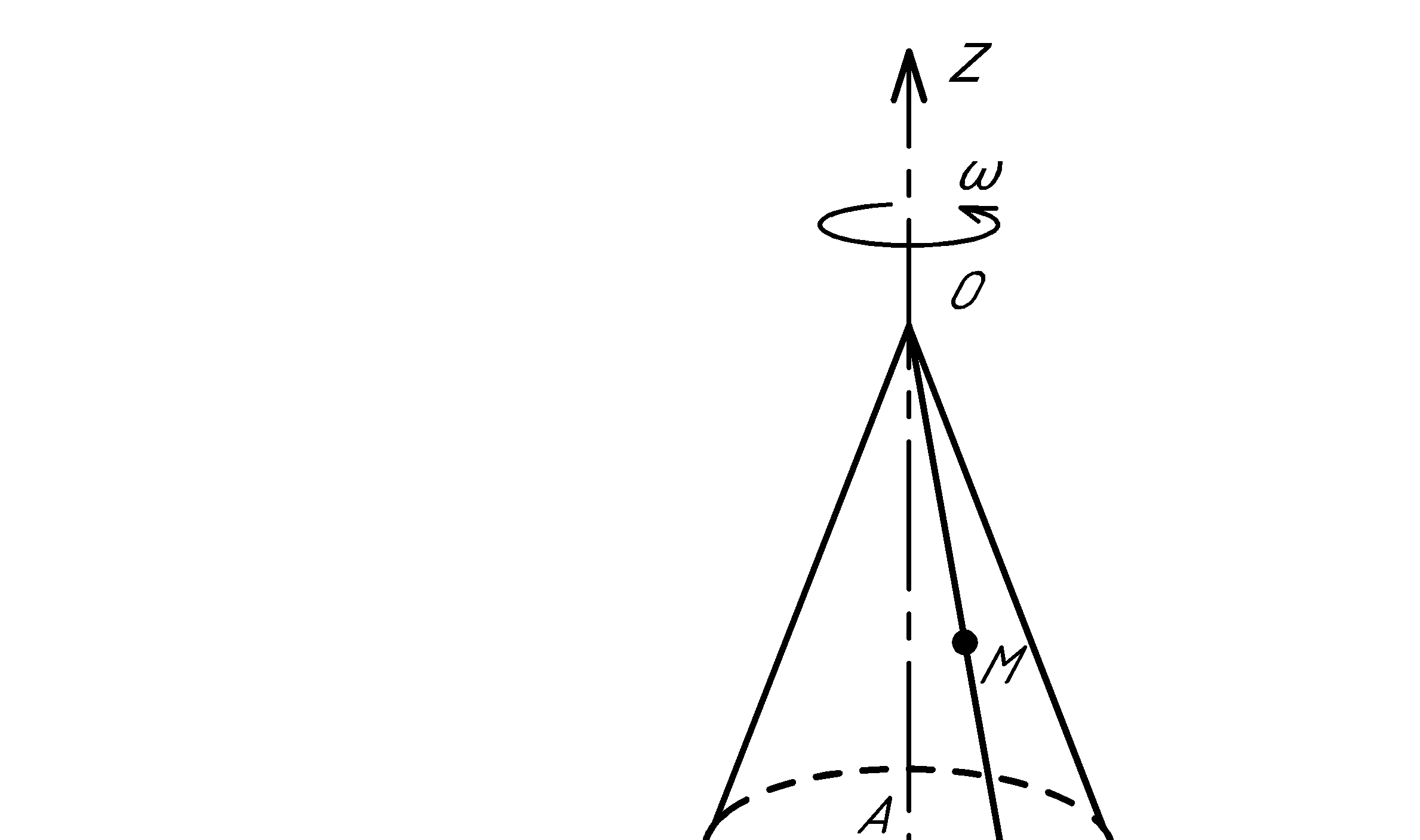
  Таблица 67

 

№
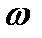
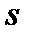
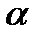
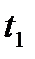
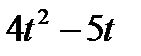
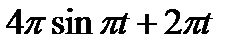
30° 1.5
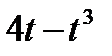
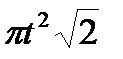
45°
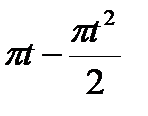
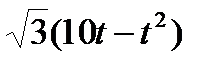
60° 2.5
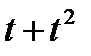
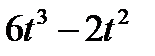
30° 2.5
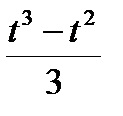
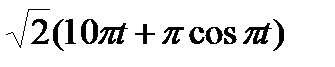
45° 2.5
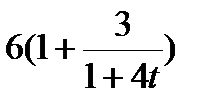
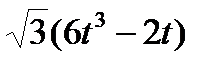
60°
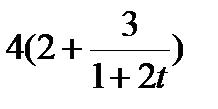
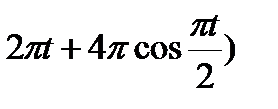
30°
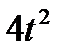
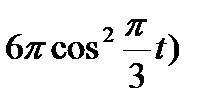
45°
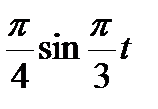
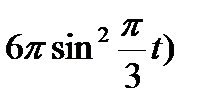
45°
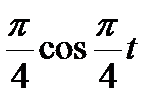
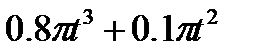
60°

 

Задача К29.

 

Кулиса ОС кулисного механизма вращается вокруг неподвижной оси О, оставаясь в верхней полуплоскости. Вдоль кулисы перемещается ползун А, соединенный шарнирно с изогнутым стержнем ABD, который движется поступательно, причем часть стержня BD перемещается по горизонтальной прямой, проходящей через точку О. Определить абсолютную скорость и абсолютное ускорение стержня АВ при заданном значении угла поворота φ кулисы ОС, если при этом значении угла φ угловая скорость кулисы равна ω с-1, ее угловое ускорение ε=0, АВ = L см и угол ABD=150°.

Указание. Точка А в абсолютном движении перемещается по горизонтальной прямой, отстоящей от точки О на расстоянии AE= 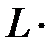sin 30° = const. Длина ОА определяется по еореме синусов из треугольника ОАВ (рис. 59, табл. 68).

 

 

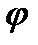
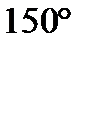
Рис. 59

 

Таблица 68

 

№
L
ω 2π 4 π 4 π 2 π 3 π 3 π 2 π 3 π 2 π 5 π
φ 120° 150° 60° 60° 120° 45° 45° 90° 135° 90°

 

Задача К30. Механизм состоит из двух параллельных валов О и O1, кривошипа ОА и кулисы O1В. Кривошип ОА = r (см) вращается с постоянной угловой скоростью ω (с-1). Конец А кривошипа соединен шарнирно с ползуном, скользящим вдоль прорези кулисы. Определить угловую скорость и угловое ускорение кулисы в момент t1 сек, если расстояние OO1 = а (см) (рис. 60, табл. 69).

 

 

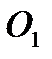
Рис. 60

 

Таблица 69

 

№
a 40√2
r 30√3
φ 0° 150° 120° 135° 240° 270° 180° 60° 90° 60°
ω 3π π 2 π 2 π 3 π 2 π

 

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.