
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Скорость – физическая величина, равная отношению перемещения тела R к промежутку времени t ,в течение которого это перемещение совершалось.
Скорость – физическая величина, равная отношению перемещения тела R к промежутку времени t ,в течение которого это перемещение совершалось.
V = 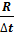
Скорость – векторная величина. Если скорость движения тела постоянна, то движение называют равномерным. В этом случае R =S , и V= S/  t.
t.
В системе СИ единица измерения скорости 1м/с.
Графиком скорости при прямолинейном равномерном движении является прямая линия , параллельная по оси времени(рис.6).
V
V1
t рис.6
Пусть тело движется со скоростью V1 в течении времени t1.Постоим график зависимости скорости от времени(рис.6*)
| V |
| V1 |
| t1 |
| t |
| (рис.6*) |
Обратим внимание, что площадь заштрихованной фигуры численно равна пути , пройденному телом за время t1.
· Часто тело участвует одновременно в нескольких движениях, например человек переплывает реку со скоростью V1,при этом его сносит течением со скоростью В этом случае человек относительно земли будет двигаться со скоростью V, являющейся результатом векторного сложения скоростей V1 и V1(рис.7а)
Другой пример: человек идёт по вагону в направлении, противоположном движению поезда, со скоростью V1;при этом смещаясь вместе с поездом со скоростью V2( рис.7в), в этом случае скорость человека относительно земли определится разностью скоростей V2 и V 1.
| V=V1 + V2 V=V2-V1 |
| Рис.7(в) |
| V1 |
| V2 |

| V1 |
| V |
| V2 |
| V=V1 + V2 |
| Рис.7(а) * |
Если скорость тела остается постоянной , то движение называют равномерным. При равномерном движении
S=vt
Графиком зависимости пути от времени является прямая линия.
| V=7м/c |
| V= 5м/c |
| V=tgα |
| α |
| S |
| t |
| S |
| t |
Если скорость тела изменяется, то движение называют неравномерным .Одной из характеристик неравномерного движения является средняя скорость.
Автомобиль тронулся с места, разогнался до некоторой скорости , проехал равномерно, стал затормаживать перед светофором, постоял под ним, затем тронулся и так проехал расстояние S;при этом в пути он находился время t.Очевидно что движение автомобиля было неравномерным.
Чтобы найти среднюю скорость его движения необходимо расстояние, пройденное автомобилем, разделить на все время, которое он находился в пути.
Vср 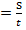
Средняя скорость - скалярная величина.
Средняя скорость – это усредненная характеристика неравномерного движения, которая не всегда полно описывает движение тела. Для более качественного описания неравномерного движения введем понятие мгновенная скорость.
Мгновенная скорость – скорость тела в конкретный момент времени, т.е. когда промежуток времени t ничтожно мал. Вектор мгновенной скорости всегда направлен по касательной к траектории движения.
Если мгновенная скорость растет, то движение называют ускоренным, если уменьшается – замедленным.Физическая величина характеризующая изменение скорости тела во времени называется ускорением.
Ускорением называют отношения изменения скорости к промежутку времени, в течение которого это изменение произошло.
 =
=  =
= 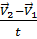
V1 – начальная скорость, V2 – конечная скорость, t – промежуток времени в течение которого
значение скорости изменилось с V1 до V2;в системе СИ измеряется в 
Ускорение векторная величина.
Рассмотрим частный случай, когда мгновенная скорость изменяется за равные промежутки времени на одну и ту же величину. Такое движение называют равноускоренным
( либо равнозамедленным), или более обобщенно – равнопеременным. При таком движении ускорение остается постоянным по величине и направлению.
Пусть при равнопеременном движении скорость в начальный момент времени (момент включения часов) равна 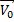 ,а по истечении времени t, скорость стала равна
,а по истечении времени t, скорость стала равна 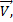 тогда:
тогда:
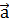 =
= 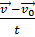
Отсюда получаем формулу зависимости скорости от времени при равнопеременном движении:

Рассмотрим частные случаи :
1.
Тело , имеющее начальную скорость 3 м/c начало двигаться с ускорением 2 м/с в течение 5с.Возьмем ось Х, по направлению совпадающую с направлением движения тела.
| X |
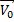
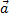

| Рис.8 |
В проекции на эту ось формула скорости получает вид
V= 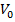 +at
+at
Подставляя в нее значения 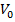 и
и 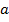 имеем :
имеем :
V=3+2t
т.е. мы получаем линейную зависимость скорости от времени. Подставив время t=5c имеем V=13м/с.
Изменение скорости можно представить графически:
| V |
| t |
Используя график можно определить значение скорости в любой момент времени без алгебраических расчетов.
2.
Автомобиль, имеющий скорость 72км/ч, начал тормозить с ускорением 2м/ 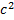 .Если выбрать ось Х , совпадающую с направление движения то очевидно что вектор ускорения направлен против движения и имеет отрицательную проекцию на ось Х (рис.10)
.Если выбрать ось Х , совпадающую с направление движения то очевидно что вектор ускорения направлен против движения и имеет отрицательную проекцию на ось Х (рис.10)
| X |

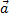

| Рис.10 |
В этом случае формула зависимости скорости от времени в проекции на ось Х принимает вид:

Переведя 72 км/ч , в СИ то получаем 20 м/c;Подставив значения 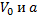 , получаем V=20 –2t. График этой зависимости имеет вид:
, получаем V=20 –2t. График этой зависимости имеет вид:
| t |
| V |
| Рис.11 |
Поскольку при равнопеременном движении скорость от времени имеет линейную зависимость то среднюю скорость движения можно рассчитать как среднее арифметическое, т.е.

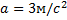
|
| t |
| V |
| t |
| V |
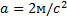
|
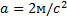
|
| Рис.12 |
| Рис.13 |
На рис.12 представлены графики равноускоренных движений с различными начальными скоростями и ускорениями.
На рис.13 представлены графики равноускоренных(1,2) и равнозамедленных (3,4) движений.
Попробуем вывести формулу для расчета пути при равноускоренном и равнозамедленном движениях.
При равноускоренном движении зависимость скорости от времени в проекции имеет вид: 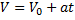
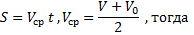
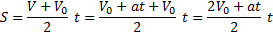
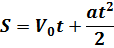
Это формула для расчета пути при равноускоренном движении.
При равнозамедленном движении зависимость скорости от времени в проекции имеет вид: 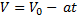
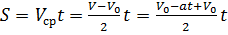
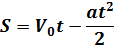
Это формула пути при равнозамедленном движении.
Перемещение при равнопеременном движении имеет вид:
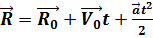 ,
,
Где 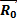 - начальное перемещение тела, которое оно совершило до момента включения часов.
- начальное перемещение тела, которое оно совершило до момента включения часов.
При равноускоренном движении с начальной скоростью 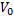 и ускорением
и ускорением 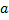 в течение времени
в течение времени 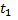 график изменения скорости имеет вид :
график изменения скорости имеет вид :
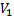
|
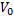
|

|
| Рис.14 |
Площадь заштрихованной трапеции равна
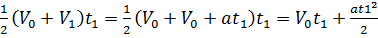
Но и путь, пройденный телом за время  ,также находится по этой формуле.
,также находится по этой формуле.
При равнозамедленном движении график имеет вид:
| V |
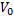
|
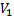
|

|
| t |
| Рис.15 |
Площадь заштрихованной трапеции :
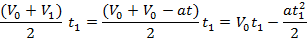
также численно равна пути пройденному телом за время  .
.
Вообще говоря, при любом неравномерном движении путь, пройденный за какой-либо промежуток времени численно равен площади фигуры, ограниченной осью времени, графиком скорости и двумя вертикальными отрезками, проведенными из точек, соответствующих началу и концу данного промежутка времени.(рис.16)
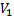
|
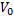
|
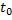
|

|
| t |
| V |
| Рис.16 |
Вернемся к формулам зависимости пути от времени при равнопеременном движении. Это зависимость носит квадратичный характер. При равноускоренном движении  ,коэффициент при старшем члене положительный графиком этой зависимости является парабола , ветви которой направлены вверх. При этом заметим что поскольку время- величина неотрицательная, то физический смысл имеет лишь правая часть параболы, находящаяся в положительных значениях времени.
,коэффициент при старшем члене положительный графиком этой зависимости является парабола , ветви которой направлены вверх. При этом заметим что поскольку время- величина неотрицательная, то физический смысл имеет лишь правая часть параболы, находящаяся в положительных значениях времени.
| S |
| t |
| Рис.17 |
При равнозамедленном движении 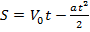 ,коэффициент при старшем члене отрицателен ,ветви направлены вниз. Но путь, в отличие от координаты, не может быть отрицательным и всегда увеличивается по мере движения, поэтому графиком пути в этом случае будет парабола, симметричная относительно оси t
,коэффициент при старшем члене отрицателен ,ветви направлены вниз. Но путь, в отличие от координаты, не может быть отрицательным и всегда увеличивается по мере движения, поэтому графиком пути в этом случае будет парабола, симметричная относительно оси t
| S |
| t |
| Рис.18 |
Частным случаем равнопеременного движения является свободное падение тел, т.е. движение тел только под действием силы тяжести. В этом случае все тела, независимо от их массы, движутся с одинаковым ускорением 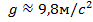 - это ускорение называют ускорением свободного падения и оно всегда направленно к центру Земли.
- это ускорение называют ускорением свободного падения и оно всегда направленно к центру Земли.
Криволинейное движение.
Вспомним, что ускорение – это физическая величина характеризующая изменение скорости тела .При криволинейном движении скорость тела изменяется по крайней мере по направлению, в общем случае она также может изменяться по величине. А значит криволинейное движение – это всегда движение с ускорением. (рис.19)
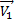
|
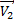
|
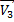
|
| Рис.19 |
Рассмотрим движение тела со скоростью , изменяющейся по величине и направлению ( рис.20). В точке 1 скорость тела 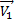 , в точке 2
, в точке 2 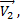 время перемещения из точки 1 в точку 2 равно t
время перемещения из точки 1 в точку 2 равно t
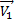
|
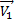
|
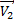
|
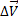
|
| Рис.20 |
Перенесем 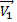 в точку 2.
в точку 2. 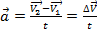 .Очевидно, что
.Очевидно, что 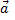 сонаправлен с
сонаправлен с 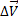 , а значит при криволинейном движении ускорение всегда направлено внутрь кривизны.
, а значит при криволинейном движении ускорение всегда направлено внутрь кривизны.

|

|
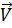
|
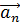
|
| Рис.21 |
Скорость при криволинейном движении изменяется по величине и направлению ( Рис.21).
Поскольку ускорение - это величина, характеризующая любое изменение скорости, то это дает нам право разложить вектор полного ускорения на две составляющих.Одна из составляющих лежит на касательной к траектории движения как и мгновенная скорость и характеризует лишь изменение величины скорости. Эта составляющая называется тангенциальным или касательным ускорением. Другая составляющая полного ускорения лежит на перпендикуляре (нормали) к мгновенной скорости и характеризует лишь изменение направления скорости. Эту составляющую называют нормальным ускорением. При этом всегда  .
.
Остановимся более подробно на частном случае криволинейного движения – равномерном движения тела по окружности.
| Рис.22 |
|
Пусть точка совершает равномерное движение по окружности R (рис.22). Мгновенная скорость V, которая в этом случае называется линейной, остается постоянной по величине. Превращение точки изменяется её угол поворота 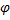 , а значит вращение точки можно охарактеризовать угловой скоростью – величиной равной углу поворота за единицу времени.
, а значит вращение точки можно охарактеризовать угловой скоростью – величиной равной углу поворота за единицу времени.

В системе СИ угол поворота (его еще называют угловым перемещением) измеряется в радианах, угловая скорость в рад/сек.
Совершив угловое перемещение  точка при этом проделала путь равный длине хорды L.
точка при этом проделала путь равный длине хорды L.
C одной стороны длина хорды 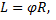 c другой
c другой 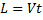 (т.к. вращение равномерное).
(т.к. вращение равномерное).
 , но
, но  .
.
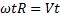
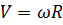
Последняя формула выражает связь между угловой и линейной скоростями.
Время за которое тело, вращающееся равномерно, совершает один полный оборот, называется периодом вращения; обозначается 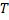 , измеряется в с.
, измеряется в с.
Величина, обратная периоду, и показывающая количество оборотов за единицу времени, называется частотой вращения, обозначается 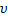 (ню),в системе СИ измеряется в Гц.
(ню),в системе СИ измеряется в Гц.
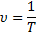
За один период угловое перемещение тела равно 2 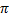 , и оно при этом проходит путь равный длине окружности 2
, и оно при этом проходит путь равный длине окружности 2 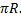
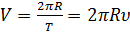
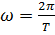 = 2
= 2 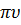
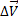
|
| О |

|

|

|

|
| R |
| Vt |
| a |
| b |
| O |
| Рис.23 |
Найдем ускорение при равномерном движении тела по окружности. Возьмем очень малый промежуток времени t, в течение которого тело переместилось из точки a в точку b. (рис.23)
Промежуток времени возьмем настолько малым, чтобы длина длины дуги ab и длина хорды ab были почти одинаковы. Тогда путь тела  равен длине хорды.
равен длине хорды.
Перенесем в точку O вектора линейных скоростей из точек a и b. Из определения ускорения 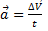 , следовательно
, следовательно 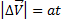
Треугольники подобны, следовательно 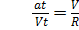

Скорость не меняется по величине, а значит проекция ускорения на вектор скорости равна 0. При равномерном вращении по окружности тело обладает лишь нормальным (центростремительным) ускорением.
На всякое тело, выброшенное за пределы Земной атмосферы действуют только силы тяготения со стороны Земли, Солнца и др. небесных тел.В зависимости от начальной скорости, сообщенной телу при его вылете из атмосферы, дальнейшая судьба тела может быть различной: при малых скоростях тело может упасть обратно на Землю, при больших – стать искусственным спутником Земли и вращаться по круговой или эллиптической орбите, при ещё больших скоростях – по параболической орбите покинуть Землю и стать спутником Солнца, а при еще больших – по гиперболической орбите покинуть Солнечную систему.
Скорость, при которой тело начинает вращаться по круговой орбите Земли, называют первой космической скоростью. Попробуем ее рассчитать.
Если высота спутника небольшая по сравнению с радиусом Земли, то для простоты расчетов пренебрежем этой высотой. Но при этом сила тяжести всегда будет направлена к центру Земли, и ускорение свободного падения будет являться нормальным. Тогда
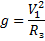
 - первая космическая скорость
- первая космическая скорость
 двигаясь с этой скоростью спутник огибал бы Землю за 84 мин.и 12с.
двигаясь с этой скоростью спутник огибал бы Землю за 84 мин.и 12с.
Спутник, вращающийся вокруг Земли вблизи земной поверхности, имеет ускорение  ,направления к центру Земли , т.е. это свободное падение под действием силы тяжести. Следовательно движения спутника аналогично движению пули или баллистической ракеты. Разница лишь в том , что горизонтальная скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли, а его свободное падение сводится к огибанию земной поверхности.
,направления к центру Земли , т.е. это свободное падение под действием силы тяжести. Следовательно движения спутника аналогично движению пули или баллистической ракеты. Разница лишь в том , что горизонтальная скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли, а его свободное падение сводится к огибанию земной поверхности.
Из формулы 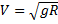 следует, что если скорость тела будет меньше первой космической, то R окажется меньше
следует, что если скорость тела будет меньше первой космической, то R окажется меньше 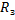 , а значит тело упадет на землю.
, а значит тело упадет на землю.
При скорости большей первой космической радиус кривизны траектории R больше  и тело движется по эллиптической орбите.
и тело движется по эллиптической орбите.
Последнее справедливо до значения скорости 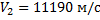 , которую называют второй космической скоростью. При этой и больших скоростях тело переходит на параболическую орбиту и покидает Землю.
, которую называют второй космической скоростью. При этой и больших скоростях тело переходит на параболическую орбиту и покидает Землю.
(расчет второй космической скорости смотри Ландсберг т.1 параграф 125 через закон сохранения энергии)
Вернемся к формуле первой космической скорости. В действительности тело не может двигаться по орбите равной радиусу Земли из-за большого сопротивления воздуха вблизи ее поверхности. Найдем, какова должна быть скорость движения по круговой орбите радиуса R, большего 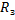 ; при этом учтем что значение ускорения свободного падения убывает при удалении от центра Земли в отношении обратно пропорциональном квадрату расстояния от центра Земли.
; при этом учтем что значение ускорения свободного падения убывает при удалении от центра Земли в отношении обратно пропорциональном квадрату расстояния от центра Земли.

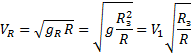
Таким образом при увеличении радиуса орбиты величина скорости, необходимой для вращения вокруг Земли уменьшается.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|