
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица неопределенных интегралов
Таблица неопределенных интегралов
| Неопределённый интеграл | Первообразная | Неопределённый интеграл | Первообразная | |
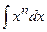 ; ; 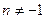
| 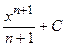
| 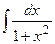
| 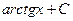
| |
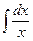 ; ; 
| 
| 
| 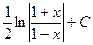
| |
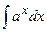 ; ; 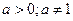
| 
| 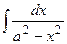
| 
| |
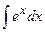
| 
| 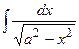
| 
| |
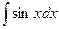
| 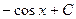
| 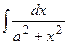
| 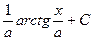
| |

| 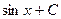
| 
| 
| |
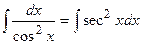
| 
| 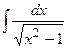
| 
| |
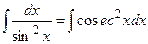
| 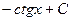
| 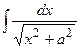
| 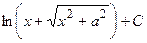
| |

| 
| 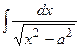
| 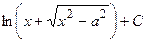
| |
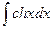
| 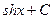
| 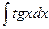
| 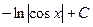
| |

| 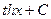
| 
| 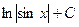
| |

| 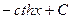
| 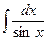
| 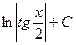
| |

| 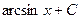
| 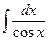
| 
|
Методы интегрирования
- Интегрирование по частям:
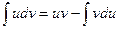 , где
, где 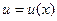 и
и 
- Интегрирование простых дробей:
2.1. 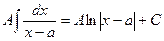 , где А, а – вещественные числа
, где А, а – вещественные числа
2.2.  , где А, а – вещественные числа; к=2, 3, 4, …
, где А, а – вещественные числа; к=2, 3, 4, …
2.3. 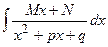 , где M, N, p, q – вещественные числа
, где M, N, p, q – вещественные числа
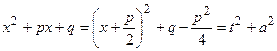 , где
, где 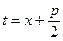 .
.
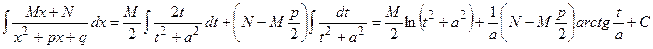
2.4. 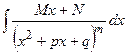 , где M, N, p, q – вещественные числа; m=2, 3, 4, …
, где M, N, p, q – вещественные числа; m=2, 3, 4, …
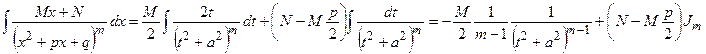 ,
,
Где 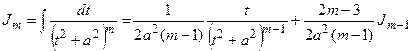 - рекуррентная формула
- рекуррентная формула
- Интегрирование правильных дробей:
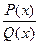 - правильная рациональная дробь
- правильная рациональная дробь
Если знаменатель разложен на простые множители 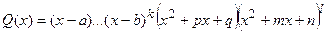 , то исходную дробь можно представить в виде суммы простых дробей:
, то исходную дробь можно представить в виде суммы простых дробей:
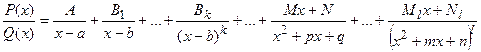 , где
, где 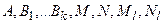 - неопределенные коэффициенты. Для их определения все дроби приводят к общему знаменателю
- неопределенные коэффициенты. Для их определения все дроби приводят к общему знаменателю 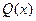 , а затем приравнивают в числителе коэффициенты справа и слева при одинаковых степенях x .
, а затем приравнивают в числителе коэффициенты справа и слева при одинаковых степенях x .
- Интегрирование неправильных дробей:
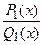 - неправильная рациональная дробь; интегрирование неправильных дробей сводится к интегрированию правильной дроби
- неправильная рациональная дробь; интегрирование неправильных дробей сводится к интегрированию правильной дроби 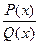 путем выделения целой части
путем выделения целой части 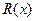 , т.е.:
, т.е.:  , где
, где 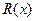 - многочлен.
- многочлен. - Интегрирование простейших иррациональностей:
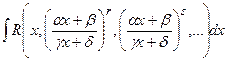 , где r, s – рациональные числа. Применяется метод рационализации подынтегрального выражения с помощью замены:
, где r, s – рациональные числа. Применяется метод рационализации подынтегрального выражения с помощью замены: 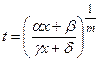 , где m – наименьший общий знаменатель показателей r и s .
, где m – наименьший общий знаменатель показателей r и s . - Интеграл от дифференциального бинома:
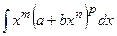 , где a, b – постоянные; m, n, p – рациональные числа.
, где a, b – постоянные; m, n, p – рациональные числа.
Используется метод рационализации подынтегрального выражения по теореме Чебышева:
6.1. Если p – целое число, то применяется подстановка 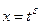 , где s - наименьший общий знаменатель дробей m и n.
, где s - наименьший общий знаменатель дробей m и n.
6.2. Если 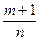 – целое число, то применяется подстановка
– целое число, то применяется подстановка 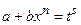 , где s - знаменатель дроби p.
, где s - знаменатель дроби p.
6.3. Если 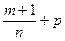 – целое число, то применяется подстановка
– целое число, то применяется подстановка 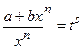 , где s - знаменатель дроби p.
, где s - знаменатель дроби p.
7. Интеграл вида 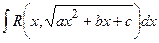 рационализуется с помощью подстановок Эйлера:
рационализуется с помощью подстановок Эйлера:
7.1. Если 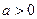 , то применяется подстановка
, то применяется подстановка 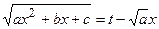 , откуда
, откуда 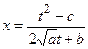
7.2. Если  , то применяется подстановка
, то применяется подстановка 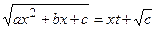
7.3. Если  , где
, где 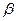 и
и  - различные действительные корни квадратного трехчлена, то применяется подстановка
- различные действительные корни квадратного трехчлена, то применяется подстановка 
8. Интегрирование тригонометрических функций:
8.1. Интеграл вида  реализуется с помощью универсальной подстановки:
реализуется с помощью универсальной подстановки:  . Тогда
. Тогда 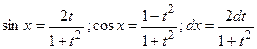
8.2.1. Если функция 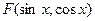 нечетная относительно синуса, то применима подстановка:
нечетная относительно синуса, то применима подстановка: 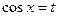 . Тогда
. Тогда 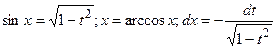 .
.
8.2.2. Если функция 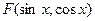 нечетная относительно косинуса, то применима подстановка:
нечетная относительно косинуса, то применима подстановка:  . Тогда
. Тогда 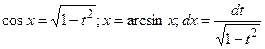 .
.
8.2.3. Если функция 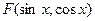 четная относительно синуса и косинуса, то применима подстановка:
четная относительно синуса и косинуса, то применима подстановка: 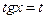 . Тогда
. Тогда  .
.
8.3. При интегрировании произведений синусов и косинусов используются следующие тригонометрические формулы:
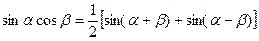 ;
; 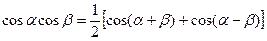 ;
;
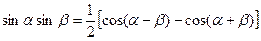
8.4. Вычисление интегралов вида 
8.4.1. Если m – нечетное положительное целое число, то применима подстановка: 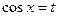 ;
; 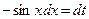 .
.
Если n – нечетное положительное целое число, то применима подстановка: 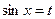 ;
; 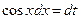 .
.
8.4.2. Если m+n – четное отрицательное целое число, то применима подстановка: 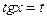 ;
; 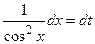 .
.
8.4.3. Если m и n – четное неотрицательные числа, то применимы формулы понижения порядка:
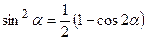 ;
; 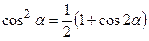
9. Интегрирование гиперболических функций:
При интегрировании гиперболических функций применяют следующие формулы:
 ;
; 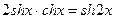 ;
; 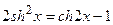 ;
; 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|