
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ (1) ДЛЯ СТУДЕНТОВ 2 КУРСА
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ (1) ДЛЯ СТУДЕНТОВ 2 КУРСА
ФАКУЛЬТЕТА ИНФОРМАТИКИ И УПРАВЛЕНИЯ
Задание 1 . Вычислить неопределенные интегралы.
1. а) 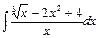 ,б)
,б) 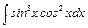 , в)
, в) 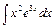 , г)
, г) 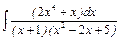 , д)
, д) 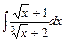 .
.
2. а) 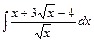 ,б)
,б) 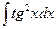 ,в)
,в) 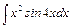 , г)
, г) 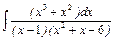 , д)
, д) 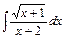 .
.
3. а) 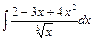 , б)
, б) 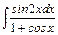 , в)
, в) 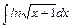 , г)
, г) 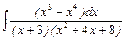 , д)
, д) 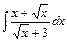 .
.
4. а) 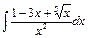 , б)
, б) 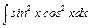 , в)
, в) 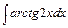 , г)
, г) 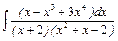 , д)
, д)  .
.
5. а) 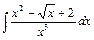 , б)
, б) 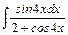 , в)
, в) 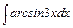 , г)
, г) 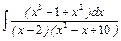 , д)
, д) 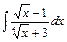 .
.
6. а) 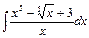 , б)
, б) 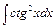 , в)
, в) 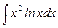 , г)
, г) 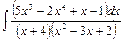 , д)
, д) 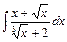 .
.
7. а) 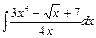 , б)
, б) 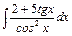 ,в)
,в) 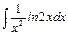 , г)
, г) 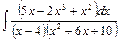 , д)
, д) 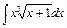 .
.
8. а) 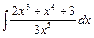 , б)
, б) 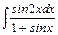 , в)
, в) 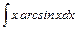 , г)
, г) 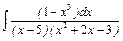 , д)
, д) 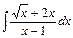 .
.
9. а) 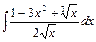 , б)
, б) 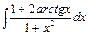 , в)
, в) 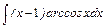 , г)
, г) 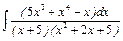 , д)
, д) 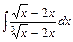 .
.
10.а) 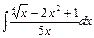 , б)
, б) 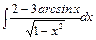 , в)
, в) 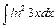 , г)
, г) 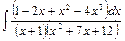 , д)
, д) 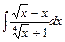 .
.
11.а) 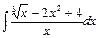 , б)
, б) 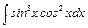 , в)
, в) 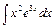 , г)
, г) 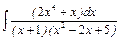 , д)
, д) 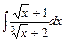 .
.
12.а) 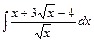 , б)
, б) 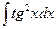 , в)
, в) 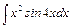 , г)
, г) 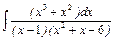 , д)
, д) 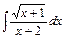 .
.
13.а) 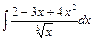 , б)
, б) 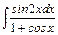 , в)
, в) 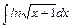 , г)
, г) 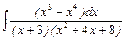 , д)
, д) 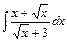 .
.
14.а) 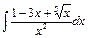 , б)
, б) 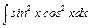 , в)
, в) 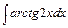 , г)
, г) 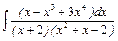 , д)
, д)  .
.
15.а) 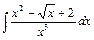 , б)
, б) 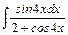 , в)
, в) 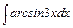 , г)
, г) 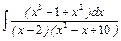 , д)
, д) 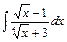 .
.
16.а) 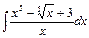 , б)
, б) 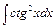 , в)
, в) 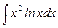 , г)
, г) 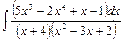 , д)
, д) 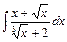 .
.
17.а) 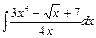 , б)
, б) 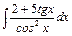 , в)
, в) 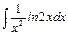 г)
г) 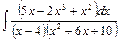 , д)
, д) 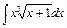 .
.
18.а) 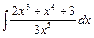 , б)
, б) 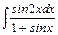 , в)
, в) 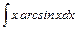 , г)
, г) 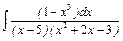 , д)
, д) 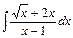 .
.
19.а) 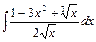 , б)
, б) 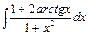 , в)
, в) 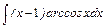 , г)
, г) 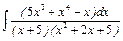 , д)
, д) 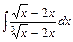 .
.
20.а) 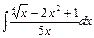 , б)
, б) 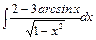 , в)
, в) 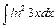 , г)
, г) 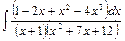 , д)
, д) 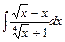 .
.
21.а) 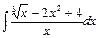 , б)
, б) 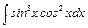 , в)
, в) 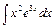 , г)
, г) 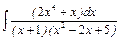 , д)
, д) 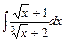 .
.
22.а) 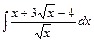 , б)
, б) 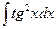 , в)
, в) 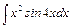 , г)
, г) 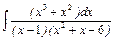 , д)
, д) 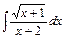 .
.
23.а) 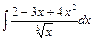 , б)
, б) 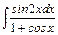 , в)
, в) 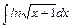 , г)
, г) 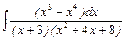 , д)
, д) 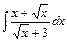 .
.
24. а) 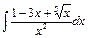 ,б)
,б) 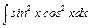 , в)
, в) 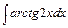 , г)
, г) 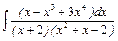 , д)
, д)  .
.
25.а) 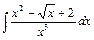 , б)
, б) 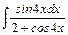 , в)
, в) 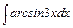 , г)
, г) 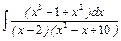 , д)
, д) 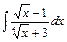 .
.
Задание 2. Найти общее решение дифференциального уравнения.
1. а) 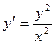 ; б)
; б) 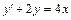 ;
;
2. а) 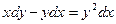 ; б)
; б) 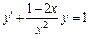 .
.
3. а) 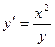 ;б)
;б) 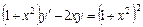 ;.
;.
4. а) 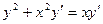 ; б)
; б) 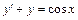 ;
;
5. а) 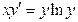 ; б)
; б) 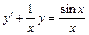 ;.
;.
6. а) 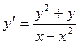 ; б)
; б) 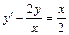 ; .
; .
7. а) 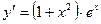 ; б)
; б) 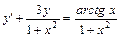 ;.
;.
8. а) 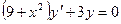 ; б)
; б) 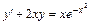 ;
;
9. а) 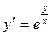 ; б)
; б) 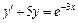 ;
;
10. а) 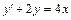 ; б)
; б) 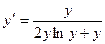 ;
;
11. а) 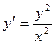 ; б)
; б) 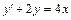 ;
;
12. а) 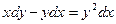 ; б)
; б) 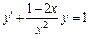 .
.
13. а) 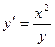 ;б)
;б) 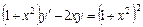 ;.
;.
14. а) 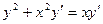 ; б)
; б) 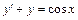 ;
;
15. а) 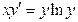 ; б)
; б) 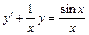 ;.
;.
16. а) 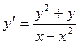 ; б)
; б) 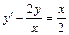 ; .
; .
17. а) 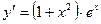 ; б)
; б) 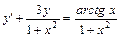 ;.
;.
18. а) 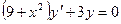 ; б)
; б) 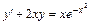 ;
;
19. а) 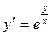 ; б)
; б) 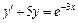 ;
;
20. а) 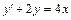 ; б)
; б) 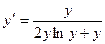 ;
;
21. а) 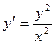 ; б)
; б) 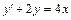 ;
;
22. а) 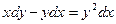 ; б)
; б) 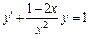 .
.
23. а) 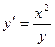 ;б)
;б) 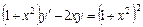 ;.
;.
24. а) 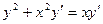 ; б)
; б) 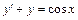 ;
;
25 а) 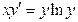 ; б)
; б) 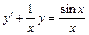 ;.
;.
Задание 3. Для данного дифференциального уравнения второго порядка найти частное решение, удовлетворяющее заданным начальным условиям.
1. 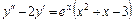 ,
, 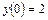 ,
, 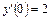 .
.
2. 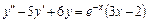 ,
, 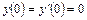 .
.
3. 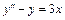 ,
, 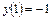 ,
, 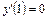 .
.
4. 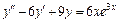 ,
, 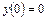 ,
, 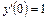 .
.
5. 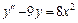 ,
, 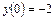 ,
, 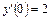 .
.
6. 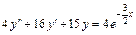 ,
, 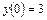 ,
, 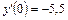 .
.
7. 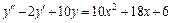 ,
, 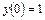 ,
, 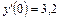 .
.
8. 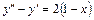 ,
, 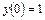 ,
, 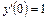 .
.
9. 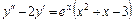 ,
, 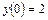 ,
, 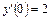 .
.
10. 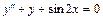 ,
,  .
.
11. 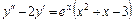 ,
, 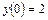 ,
, 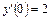 .
.
12. 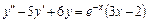 ,
, 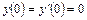 .
.
13. 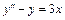 ,
, 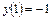 ,
, 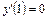 .
.
14. 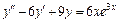 ,
, 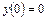 ,
, 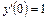 .
.
15. 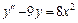 ,
, 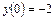 ,
, 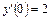 .
.
16. 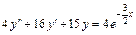 ,
, 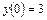 ,
, 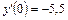 .
.
17. 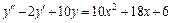 ,
, 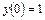 ,
, 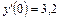 .
.
18. 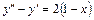 ,
, 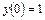 ,
, 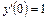 .
.
19. 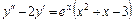 ,
, 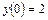 ,
, 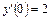 .
.
20. 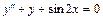 ,
,  .
.
21. 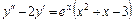 ,
, 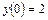 ,
, 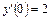 .
.
22. 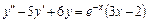 ,
, 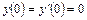 .
.
23. 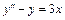 ,
, 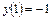 ,
, 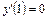 .
.
24. 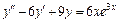 ,
, 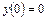 ,
, 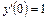 .
.
25. 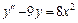 ,
, 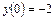 ,
, 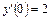 .
.
Задание 4. Дана функция 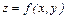 . Показать, что
. Показать, что 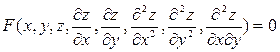 .
.
1. 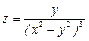 ;
; 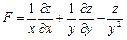 ;
;
2. 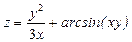 ;
; 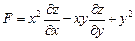 ;
;
3. 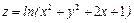 ;
; 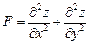 ;
;
4. 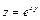 ;
; 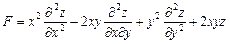 ;
;
5. 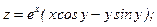
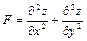 ;
;
6. 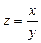 ;
; 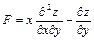 ;
;
7. 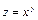 ;
; 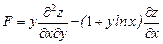 ;
;
8. 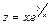 ;
; 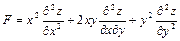 ;
;
9. 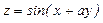 ;
; 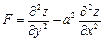 ;
;
10. 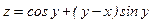 ;
; 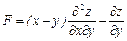 .
.
11. 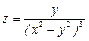 ;
; 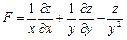 ;
;
12. 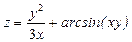 ;
; 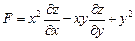 ;
;
13. 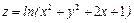 ;
; 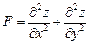 ;
;
14. 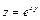 ;
; 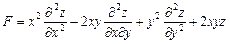 ;
;
15. 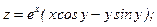
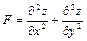 ;
;
16. 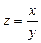 ;
; 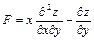 ;
;
17. 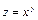 ;
; 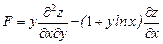 ;
;
18. 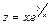 ;
; 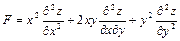 ;
;
19. 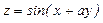 ;
; 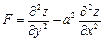 ;
;
20. 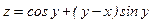 ;
; 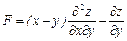
21. 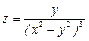 ;
; 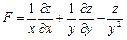 ;
;
22. 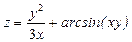 ;
; 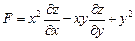 ;
;
23. 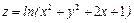 ;
; 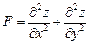 ;
;
24. 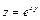 ;
; 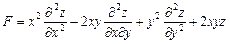 ;
;
25. 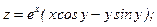
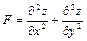 .
.
Задание 5. Дана функция 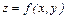 и точка M0(x0;y0). С помощью дифференциала вычислить приближенное значение функции в данной точке.
и точка M0(x0;y0). С помощью дифференциала вычислить приближенное значение функции в данной точке.
1. 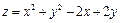 ; M0(1,08;1,94);
; M0(1,08;1,94);
2. 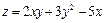 ; M0(3,04;3,95);
; M0(3,04;3,95);
3. 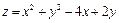 ; M0(2,98;2.05);
; M0(2,98;2.05);
4. 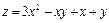 ; M0(1,06;2,92);
; M0(1,06;2,92);
5. 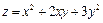 ; M0(2,94;1,07);
; M0(2,94;1,07);
6. 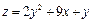 ; M0(1,96;1,04);
; M0(1,96;1,04);
7. 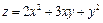 ; M0(0,96;1,95);
; M0(0,96;1,95);
8. 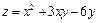 ; M0(3,96;1,03);
; M0(3,96;1,03);
9. 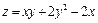 ; M0(0,97;2,03);
; M0(0,97;2,03);
10. 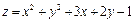 ; M0(2,98;3,91).
; M0(2,98;3,91).
11. 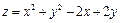 ; M0(1,08;1,94);
; M0(1,08;1,94);
12. 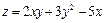 ; M0(3,04;3,95);
; M0(3,04;3,95);
13. 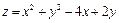 ; M0(2,98;2.05);
; M0(2,98;2.05);
14. 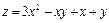 ; M0(1,06;2,92);
; M0(1,06;2,92);
15. 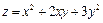 ; M0(2,94;1,07);
; M0(2,94;1,07);
16. 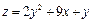 ; M0(1,96;1,04);
; M0(1,96;1,04);
17. 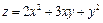 ; M0(0,96;1,95);
; M0(0,96;1,95);
18. 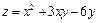 ; M0(3,96;1,03);
; M0(3,96;1,03);
19. 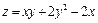 ; M0(0,97;2,03);
; M0(0,97;2,03);
20. 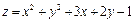 ; M0(2,98;3,91).
; M0(2,98;3,91).
21. 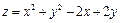 ; M0(1,08;1,94);
; M0(1,08;1,94);
22. 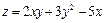 ; M0(3,04;3,95);
; M0(3,04;3,95);
23. 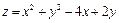 ; M0(2,98;2.05);
; M0(2,98;2.05);
24. 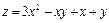 ; M0(1,06;2,92);
; M0(1,06;2,92);
25. 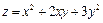 ; M0(2,94;1,07).
; M0(2,94;1,07).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|