Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Построение графиков 3-х видов в электронной таблице Excel

Построение графиков 3-х видов в электронной таблице Excel

1. Построить несколько графиков параметрически заданной функции при разных значениях конcтант а, b, l. Оси графика – х и y, которые зависят от аргумента t или j.

№	Название кривой	Вид графика	Параметри­ческие уравнения	Диапазон аргумента	Кол-во граф.	Значения констант
	Циклоида		x = a×(t - sin t) y = a×(1 - cos t)	t Î 0 ¸ 6×p шаг 0,5		a = 1; 1.25;  1.5; 1.75; 2
	Циклоида		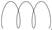x = a×(t - l×sin t) y = a×(1 - l×cos t)	t Î 0 ¸ 6×p шаг 0,5		a = 2 l = 0.4; 0.7; 1.0;  1.3; 1.6; 2.0
	Трохоида		x = a×t - b×sin t y = a - b×cos t	t Î 0 ¸ 10×p шаг 0,1		a = -1 b = 0.1; 1; 2; 3; 4
	Эпитрохоида		x = a×cos (l×t) - b×cos (t + l×t) y = a×sin (l×t) - b×sin (t + l×t)	t Î 0 ¸ 10×p шаг 0,5		a = 0; 1; 2; 3; 10; 15     b = 2   l = 0.25
	Гипотрохоида		x = a×cos (l×t) - b×cos (t - l×t) y = a×sin (l×t) - b×sin (t - l×t)	t Î 0 ¸ 10×p шаг 0,5		a = 0; 1; 2; 3; 10; 15     b = 2   l = 0.25
	Декартов лист		x = a×t / (1 + t3) y = a× t2 / (1 + t3)	t Î -6 ¸ 6 шаг 0,3		a = 1; 2; 3; 4; 5; 6
	Циссоида Диоклеса		x = a× t2 / (1 + t2) y = a× t3 / (1 + t2)	t Î -6 ¸ 6 шаг 0,2		a = 1; 2; 3; 4; 5; 6
	Строфоида		x = a× (t2 - 1) / (t2 + 1) y = a×t×(t2 - 1) / (t2 + 1)	t Î -6 ¸ 6 шаг 0,2		a = 1; 2; 3; 4; 5; 6
	Конхоида Никомеда		x = a + b×cos t y = a×tg t + b×sin t	t Î 0 ¸ 10 шаг 0,2		a = 2 b = 1; 10; 30; 50; 90
	Улитка Паскаля		x = a×cos2 t + b×cos t y = a× cos t ×sin t + b×sin t	t Î 0 ¸ 2×p шаг 0,1		a = 1; 2; 3; 4; 5; 6 b = 3
	Эпици­клоида		x = (a + b)×cos j - a×cos[(a + b)×j/a] y = (a + b)× sin j - a ×sin[(a + b)×j/a]	j Î 0 ¸ 2×p Шаг 0,1		a = 1 b = 1; 2; 3; 4; 5; 6
	Эпици­клоида		x = (a + b)×cos j - l×a×cos[(a + b)×j/a] y = (a + b)× sin j - l×a ×sin[(a + b)×j/a]	j Î 0 ¸ 10×p Шаг 0,2		a = 3; b = 4 l = 0.5; 0.7; 1;  1.5; 2; 3
	Эпици­клоида		x = (a + b)×cos j - l×a×cos[(a + b)×j/a] y = (a + b)× sin j - l×a ×sin[(a + b)×j/a]	j Î 0 ¸ 2×p Шаг 0,1		a = 1; b = 4 l = 0.5; 1; 1.5; 2; 4; 6
	Эпици­клоида		x = (a + b)×cos j - l×a×cos[(a + b)×j/a] y = (a + b)× sin j - l×a ×sin[(a + b)×j/a]	j Î 0 ¸ 2×p Шаг 0,1		a = 7; b = 4 l = 0.5; 1; 2; 4; 6; 8
	Гипоци­клоида		x = (b - a)×cos j - a×cos[(b - a)×j/a] y = (b - a)× sin j - a ×sin[(b - a)×j/a]	j Î 0 ¸ 2×p Шаг 0,1		a = 1 b = 1.5; 2.5; 3;  3.5; 4; 5
	Гипоци­клоида		x = (b - a)×cos j - a×cos[(b - a)×j/a] y = (b - a)× sin j - a ×sin[(b - a)×j/a]	j Î 0 ¸ 6×p Шаг 0,5		a = 1.5; 2; 2.5;  3; 3,5; 4 b = 1
	Гипоци­клоида		x = (b - a)×cos j - l×a×cos[(b - a)×j/a] y = (b - a)× sin j - l×a ×sin[(b - a)×j/a]	j Î 0 ¸ 2×p Шаг 0,1		a = 1; b = 4 l = 0.5; 1; 1.5; 2; 3; 4
	Гипоци­клоида		x = (b - a)×cos j - l×a×cos[(b - a)×j/a] y = (b - a)× sin j - l×a ×sin[(b - a)×j/a]	j Î 0 ¸ 10×p Шаг 0,2		a = 5; b = 2 l = 0.2; 0.5; 0.7;  1; 1.5; 2
	Спираль		x = a×t×cos t y = b×t×sin t	t Î 0 ¸ 10×p Шаг 0,5		a = 2 b = -2; -1; 1; 2; 3; 4
	Гиперболич. спираль		x = (a×cos t) / t y = (b ×sin t) / t	t Î -6 ¸ 6 Шаг 0,3		a = 2 b = 1; 2; 3; 4; 5
	Гиперболич. спираль		x = (a×cos t) / t y = (b ×sin t) / t	t Î 0.5 ¸ 20 Шаг 0,5		a = 3 b = 1; 2; 3; 4; 5
	Астроида		x = a×cos3 (t / 4) y = b ×sin3 (t / 4)	t Î 0 ¸ 8×p Шаг 0,1		a = 2 b = 1; 2; 3; 4; 5
	Астроида		x = a×cos3 (t – b) y = a ×sin3 t	t Î 0 ¸ 8×p Шаг 0,2		a = 2 b = 0; 1; 2; 3; 4
	Астроида		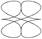x = a×cos3 (b×t ) y = a ×sin3 t	t Î 0 ¸ 8×p Шаг 0,1		a = 2 b = 0.5; 1; 1.5; 3; 3.5
	Эволь­вента		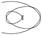x = a×cos t + a×t ×sin t y = a ×sin t + a×t×cos t	t Î -10 ¸10 Шаг 0,5		a = -2; -1; 1; 2
	Эволь­вента		x = a×cos t + a×t ×sin t y = a ×sin t + a×t×cos t	t Î 0 ¸20 Шаг 0,5		a = -2; -1; 1; 2
	Эллипс		x = a×cos t y = b ×sin t	t Î 0 ¸ 2×p Шаг 0,5		a = 7 b = 1; 4; 7; 10; 13
	Эллипс		x = a×cos(c + t) y = b ×sin(c - t)	t Î 0 ¸ 2×p Шаг 0,11		a = 3 b = 2 b = 1; 2; 3; 4; 5