
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основные формулы и теоремы.. Основные оригиналы и их изображения.
Основные формулы и теоремы.
Изображением функции 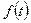 по Лапласу называется функция
по Лапласу называется функция 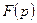 комплексного переменного
комплексного переменного 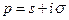 , определяемая равенством
, определяемая равенством
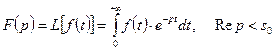
Основные оригиналы и их изображения.
1) 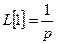 ,
, 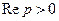 ; 5)
; 5) 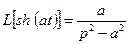 ,
, 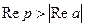 ;
;
2) 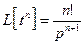 ,
, 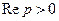 ; 6)
; 6) 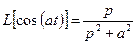 ,
, 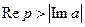 ;
;
3) 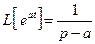 ,
, 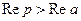 ; 7)
; 7) 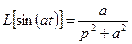 ,
, 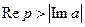 .
.
4) 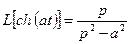 ,
, 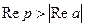 ;
;
Теорема подобия. Если 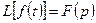 и действительное число
и действительное число  , то
, то
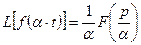 .
.
Теорема запаздывания. Если 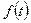 и
и 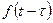 при
при 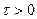 оригиналы, то при
оригиналы, то при 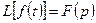 имеем
имеем
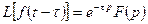 .
.
Изображение периодического оригинала. Если оригинал является периодической функцией с периодом а, т. е. 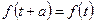 , то изображение такой функции находится по формуле:
, то изображение такой функции находится по формуле:
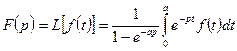
и определено в области 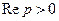 .
.
Теорема смещения (затухания). Если 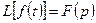 ,
, 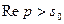 , то при любом комплексном а
, то при любом комплексном а
 ,
, 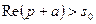 .
.
Изображение производной (дифференцирование оригинала). Если 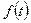 является оригиналом, причём
является оригиналом, причём 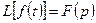 , и существуют производные
, и существуют производные 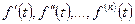 , являющиеся оригиналами, то изображение
, являющиеся оригиналами, то изображение 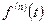 находится следующим образом:
находится следующим образом:
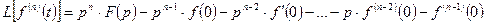 ,
,
где 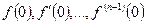 правые предельные значения функции и её производных в точке
правые предельные значения функции и её производных в точке 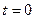 .
.
Операторное уравнение. Если
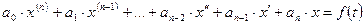 ,
,
то
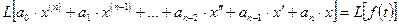
или
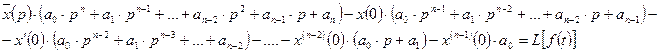
Дифференцирование изображения. Если 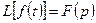 , то
, то
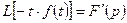 ,
,
причём, второе из этих равенств справедливо в той же полуплоскости, что и первое.
Свёрткой двух функций 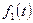 и
и 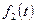 называется функция, определённая следующим равенством:
называется функция, определённая следующим равенством:
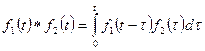 .
.
Умножение изображений. Если 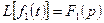 ,
, 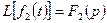 , то
, то
 или
или 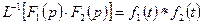 .
.
Интегрирование оригинала. Если 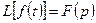 , то
, то
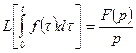 или
или 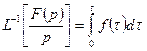 .
.
Теорема обращения. Если 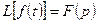 и
и 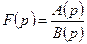 является дробно-рациональной функцией со степенью числителя, меньшей степени знаменателя и знаменатель имеет корни
является дробно-рациональной функцией со степенью числителя, меньшей степени знаменателя и знаменатель имеет корни 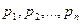 кратности
кратности 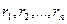 , то оригинал
, то оригинал 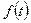 определяется по формуле:
определяется по формуле:
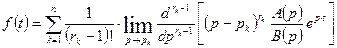 .
.
Если 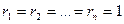 , то оригинал можно найти, пользуясь равенством:
, то оригинал можно найти, пользуясь равенством:
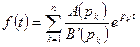 .
.
При отыскании частного решения дифференциального уравнения с нулевыми начальными условиями часто применяется формула Дюамеля.
Формула Дюамеля. Пусть 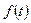 ,
, 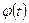 ,
, 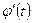 ‑ оригиналы и
‑ оригиналы и 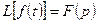 ,
, 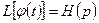 , тогда имеет место формула
, тогда имеет место формула
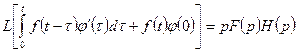 ,
,
или
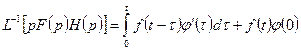 .
.
Пусть теперь нужно решить уравнение
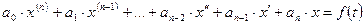
с нулевыми начальными условиями: 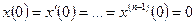 .
.
Составим вспомогательное уравнение с такими же коэффициентами 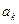 и с правой частью, равной единице:
и с правой частью, равной единице: 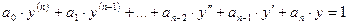 ,
,  .
.
Можно доказать, что если, как обычно, обозначить 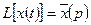 ,
, 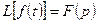 ,
, 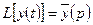 , то функции
, то функции 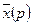 и
и 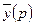 связаны соотношением
связаны соотношением 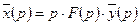 . Из этого соотношения следует, что
. Из этого соотношения следует, что 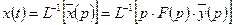 . Применяя формулу Дюамеля и учитывая, что
. Применяя формулу Дюамеля и учитывая, что 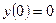 , получаем искомое решение в виде
, получаем искомое решение в виде 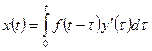 или
или 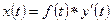 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|