Конспект урока Внутренняя энергия и работа в термодинамике

Конспект урока "Внутренняя энергия и работа в термодинамике"

Сегодня мы приступаем к изучению раздела, который называется термодинамикой. Как наука термодинамика появилась в середине 19 века после открытия закона сохранения энергии. Термодинамика изучает тепловые явления без учета молекулярного строения тел. Иначе говоря, в термодинамике все тела характеризуются макроскопическими параметрами, такими, как давление, объём и температура.

Важнейшей величиной в термодинамике является внутренняя энергия, поэтому, именно с этой темы мы и начнем. Из курса физики восьмого класса вы знаете, что внутренняя энергия тела — это суммарная кинетическая и потенциальная энергия всех частиц, входящих в данное тело.

Рассмотрим внутреннюю энергию идеального газа. Напомним, что идеальный газ — это модель реального газа, согласно которой, все молекулы этого газа двигаются беспорядочно и взаимодействуют друг с другом только при соударениях. Таким образом, мы можем сказать, что потенциальная энергия молекул идеального газа стремится к нулю. Значит, внутренняя энергия равна суммарной кинетической энергии всех молекул газа:

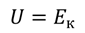
Напомним также, что недавно мы вывели формулу, характеризующую зависимость средней кинетической энергии молекул от температуры:

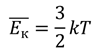
Тогда внутренняя энергия будет равна произведению средней кинетической энергии молекулы и числа молекул:

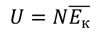
В свою очередь, число молекул определяется как произведение количества вещества и числа Авогадро:

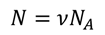
Итак, если мы подставим эти результаты в уравнение для внутренней энергии, то получим выражение, зависящее только от температуры и от количества вещества:

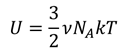
Напомним, что произведение постоянной Больцмана и постоянной Авогадро — это универсальная газовая постоянная:

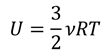
Таким образом, мы вывели уравнение, описывающее внутреннюю энергию идеального газа.

Возникает вопрос: как вычислить энергию многоатомного газа, то есть газа, который состоит не из отдельных шариков, а из более сложных молекул. В этом случае необходимо ввести понятие степени свободы. Степень свободы — это число возможных независимых движений частиц.

То есть это число включает в себя и количество возможных направлений вращения, и количество координатных осей, вдоль которых молекулы атомы газа могут двигаться. Тогда, формула для внутренней энергии немного преобразуется:

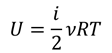
Нетрудно догадаться, что минимальное число степеней свободы в трехмерном пространстве — это три. Если мы подставим это в формулу, то получим внутреннюю энергию идеального одноатомного газа. Например, для двухатомного идеального газа число степеней свободы будет равно пяти (к движению вдоль трех координатных осей добавляется вращение вокруг двух осей).

Необходимо отметить, что для реальных газов внутренняя энергия всё же зависит не только от температуры, но и от объёма. Как мы уже говорили ранее, при сжатии газа, расстояния между его молекулами уменьшается. Это приводит к увеличению потенциальной энергии, которую мы далеко не всегда можем считать равной нулю, рассматривая реальный газ. Тем не менее, во многих случаях потенциальная энергия реальных газов пренебрежимо мала по сравнению с кинетической.

Как мы помним, изменить внутреннюю энергию любого тела можно путем совершения работы или путем теплопередачи. Об изменении энергии газа в результате теплопередачи мы поговорим чуть позже, а сейчас, давайте поговорим о понятии работы в термодинамике. Подобно тому, как в механике работа равна изменению кинетической энергии, в термодинамике, работа равна изменению внутренней энергии:

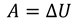
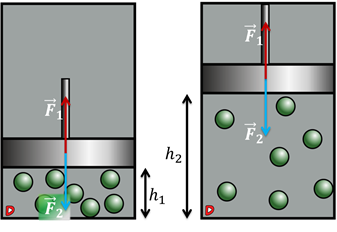
Рассмотрим пример совершения работы газом в цилиндре с подвижным поршнем. На рисунке обозначены следующие величины: сила F₁, с которой газ действует на поршень, сила F₂, с которой поршень действует на газ и два положения поршня, которые заданы через высоты h₁ и h₂.

Сразу заметим, что по третьему закону Ньютона:

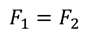
В данном примере, мы будем рассматривать изобарный процесс, то есть, процесс, проходящий при постоянном давлении газа. Тогда

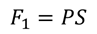
Как мы помним, работа силы равна произведению модуля силы, модуля перемещения, вызванного этой силой и косинуса угла между направлениями силы и перемещения:

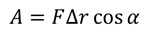
При расширении газа, поршень перемещается в направлении, совпадающем с направлением силы F₁. Тогда запишем, что работа газа в этом случае, равна

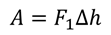
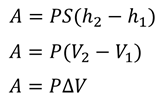
Таким образом, работа газа при изобарном расширении равна произведению давления и изменения объёма. Не трудно догадаться, что при сжатии, работа газа будет отрицательной, поскольку отрицательным будет изменение объёма. Также, в этом можно убедиться, если заметить, что при расширении сила давления газа совпадает с перемещением, то есть газ помогает движению поршня. В случае сжатия — газ, наоборот, препятствует движению поршня. В этом случае работа силы F₂, как раз-таки будет положительной.

Процессы, происходящие с газом, часто изображаются графически. Изобразим процесс, который мы только что описали в координатах P-V, то есть, график представляет собой зависимость давления от объёма.

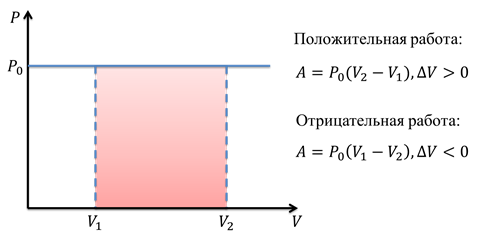
Этот график будет являться горизонтальной прямой линией, поскольку мы рассматривали изобарный процесс, при котором давление постоянно. Таким образом, работа газа будет равна площади под графиком. В нашем случае, площадь под графиком — это прямоугольник, одна из сторон которого — это значение давления, а другая — это изменение объёма. Часто на графиках направление процесса обозначается стрелочкой.

Рассматривая изохорный процесс, нетрудно убедиться, что работа будет равна нулю. Это подтверждается и графически, и логически.

На графике мы видим, что никакой площади под графиком нет. Да и чисто логически, если объём не изменился, то работа равна нулю.

Сложнее всего (на данном этапе) вычислить работу при изотермическом процессе. В P-V координатах график зависимости давления от объёма представляет собой гиперболу. Таким образом, площадь под графиком ограничена изотермой и значениями начального и конечного объёма.

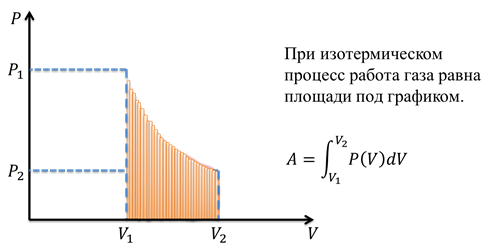
Площадь под данным графиком можно вычислить, если разделить изменение объёма на очень малые части, вычислить работы, соответствующие каждой части, а потом сложить их, чтобы получить общую работу. Математическая функция, позволяющая вычислять площади под графиком любой формы, называется интегралом, с ней вы познакомитесь позже.

Пример решения задачи.

Задача.Гелий массой 15 г нагревается от 300 К до 400 К. Найдите работу, совершенную при этом процессе, считая гелий одноатомным идеальным газом.