
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Квадратичная функция и ее график

| Дата проведения урока : «07» мая 2020 г. Предмет: Алгебра Учитель: Жарова А.А. Тема: Повторение. Квадратичная функция и ее график |
Цель урока: Подготовка к ОГЭ.
1. Квадратичная функция и ее график
Функция вида, где называется квадратичной функцией.
В уравнении квадратичной функции:
a - старший коэффициент, b - второй коэффициент, с - свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 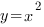 имеет вид:
имеет вид:
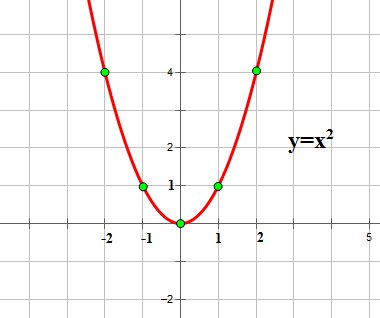 функции
функции 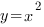 при любых значениях остальных коэффициентов при любых значениях остальных коэффициентов
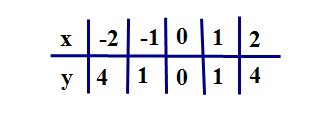
| Обратите внимание на точки, обозначенные зелеными кружками - это, так называемые "базовые точки". Чтобы найти координаты этих точек для
функции 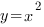 , составим таблицу. , составим таблицу.
 Внимание! Если в уравнении квадратичной функции старший коэффициент
Внимание! Если в уравнении квадратичной функции старший коэффициент 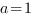 , то график квадратичной функции имеет ровно такую же форму, как график , то график квадратичной функции имеет ровно такую же форму, как график
|
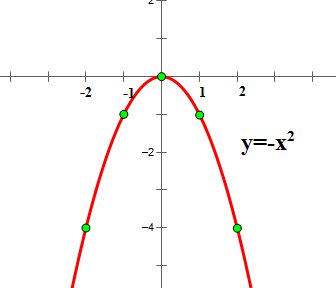
| График функции 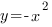 имеет вид:
Для нахождения координат базовых точек составим таблицу: имеет вид:
Для нахождения координат базовых точек составим таблицу:
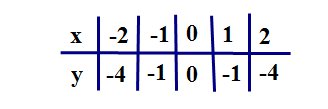 Обратите внимание, что график функции
Обратите внимание, что график функции 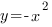 симметричен графику функции симметричен графику функции 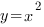 относительно оси ОХ. относительно оси ОХ.
|
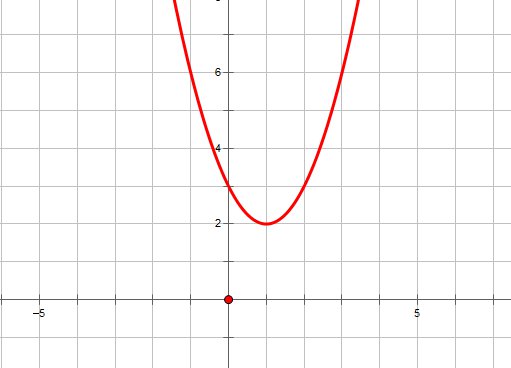
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции - значения х, в которых функция равна нулю, или нули функции. На графике нули функции 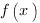 - это точки пересечения графика функции
- это точки пересечения графика функции 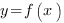 с осью ОХ.
с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции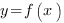 с осью ОХ, нужно решить уравнение
с осью ОХ, нужно решить уравнение  . В случае квадратичной
. В случае квадратичной 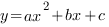 функции: нужно решить квадратное уравнение
функции: нужно решить квадратное уравнение 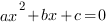 .
.
В процессе решения квадратного уравнения мы находим дискриминант : 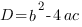 , который определяет число корней квадратного уравнения.
, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
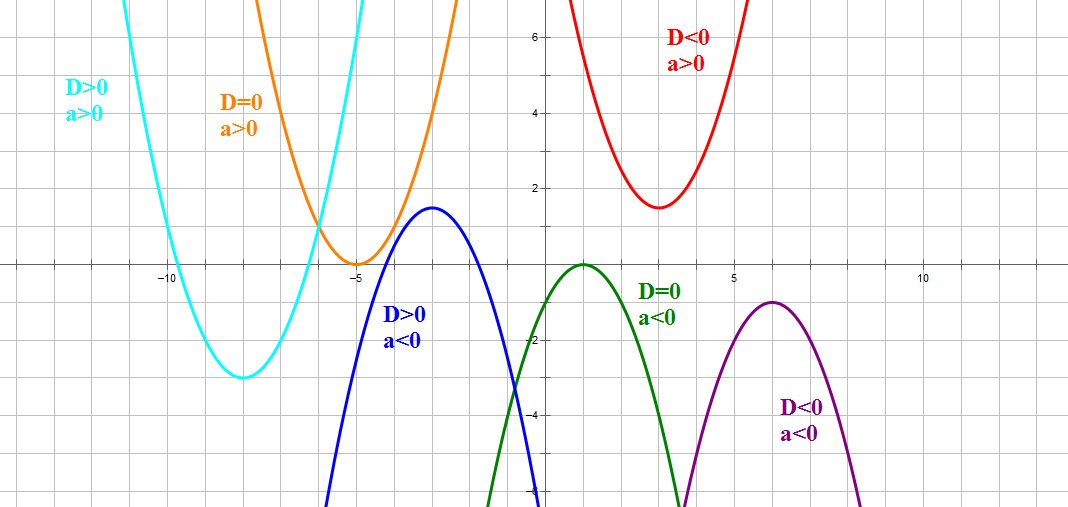
. Если 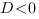  ,то уравнение у ,то уравнение у 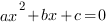 не имеет решений, и, следовательно, квадратичная парабола не имеет решений, и, следовательно, квадратичная парабола 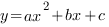 не имеет точек пересечения с осью ОХ. Если не имеет точек пересечения с осью ОХ. Если 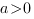  ,то график функции выглядит как-то так: ,то график функции выглядит как-то так:
| 
|
2. Если   ,то уравнение ,то уравнение 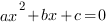 имеет одно решение, и, следовательно, квадратичная парабола имеет одно решение, и, следовательно, квадратичная парабола 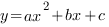 имеет одну точку пересечения с осью ОХ. Если имеет одну точку пересечения с осью ОХ. Если 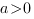  ,то график функции выглядит примерно так: ,то график функции выглядит примерно так:
| 
|
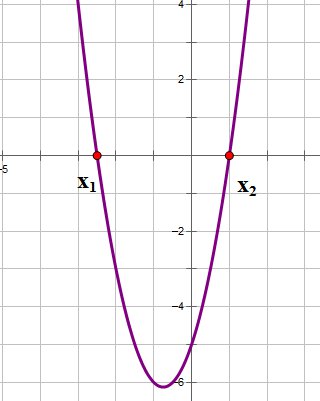
3. Если 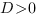  ,то уравнение у ,то уравнение у 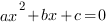 имеет два решения, и, следовательно, квадратичная парабола имеет два решения, и, следовательно, квадратичная парабола 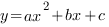 имеет две точки пересечения с осью ОХ: имеет две точки пересечения с осью ОХ:
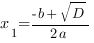 , , 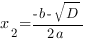 Если
Если 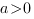  ,то график функции выглядит примерно так: ,то график функции выглядит примерно так:
| 
|
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
| Следующий важный параметр графика квадратичной функции - координаты вершины параболы: | 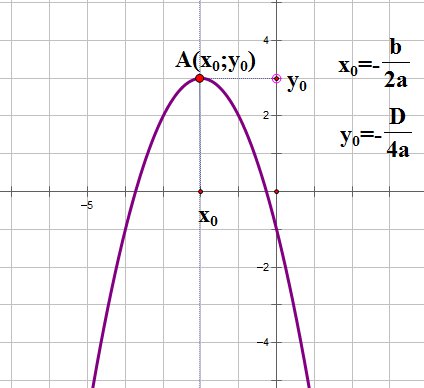
|
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы
И еще один параметр, полезный при построении графика функции - точка пересечения параболы 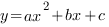 с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 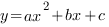 с осью OY, нужно в уравнение параболы вместо х подставить ноль: с осью OY, нужно в уравнение параболы вместо х подставить ноль: 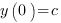 .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
| 
|

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|