Применение производной к исследованию функции

Применение производной к исследованию функции

I. Монотонность

Дана функция y = f(x). Она монотонна на некотором промежутке и имеет производную 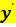в каждой точке этого промежутка:

Производная > 0 ( )	Производная < 0 ( )
Функция возрастает.	Функция убывает.

Примеры.

Для исследования функции на монотонность потребуется:
- сама функция,

- умение брать производную,

- метод интервалов.

Алгоритм:

1. Берем производную от функции.

2. Приравниваем ее к 0.

3. Решаем получившееся уравнение.

4. Применяем метод интервалов.

Решите самостоятельно:

Найдите промежутки возрастания и убывания функции:

А)

Б)

II. Точки экстремума.

1. Критические точки.Это точки, в которых производная функции = 0 или не существует.
Т.е. если f ᾽ (4) = 0, то х = 4 – критическая точка.

2. Точки экстремума.Это точки, в которых функция принимает свое наибольшее или наименьшее значения. Точки экстремума – точки минимума и точки максимума.

3.Рассмотрим график некоторой функции. Точк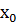и и – точки экстремума. Точка 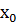– точка максимума, так как в ней график функции меняется с возрастания на убывание (вершина горочки).

Точка – точка минимума, так как в ней график функции меняется с убывание на возрастания (дно ямы).

4. Стационарные точки – точки, в которой производная функции равна 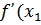0.

)=0 - стационарная точка. Таких точек может быть любое количество, зависит от вида функции.

12 Следующая ⇒