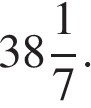- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Решение.. Решение.. Решение.. Решение.. Периоды. Долг клиента (рублей)
1.Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Какое наибольшее количество шоколадок можно получить, потратив не более 200 рублей в воскресенье?
Ответ: 7.
2.На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.
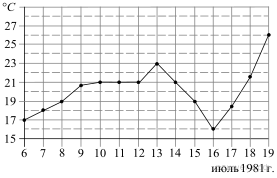
Ответ: 10.
3. 
На клетчатой бумаге с размером клетки 1  1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.
1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.
Ответ: 2,5.
4.На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Ответ: 0,33.
5.Найдите корень уравнения: 
Ответ: 14.
6.В треугольнике 
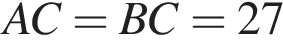 ,
,  — высота,
— высота, 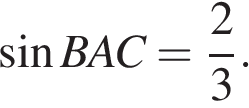 Найдите
Найдите 
Ответ: 30.
7. 
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Ответ: 4.
8. 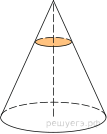
Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Ответ: 2.
9.Найдите 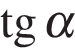 , если
, если 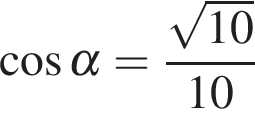 и
и 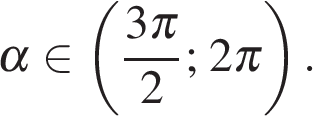
Ответ: −3.
10.Небольшой мячик бросают под острым углом 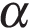 к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой
к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой  , где
, где  м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а 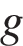 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  м/с
м/с  ). При каком наименьшем значении угла
). При каком наименьшем значении угла 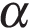 (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
(в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
Ответ: 30.
11.Вова и Гоша решают задачи. За час Вова может решить на две задачи больше, чем Гоша (при этом оба за час решают целое количество задач). Известно, что вместе они решат 33 задачи на 1 час 15 минут быстрее, чем это сделал бы один Вова. За какое время Гоша может решить 20 задач? Ответ дайте в часах.
Ответ: 2.
12.Найдите наибольшее значение функции 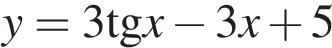 на отрезке
на отрезке 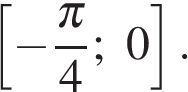
Ответ: 5.
13.а) Решите уравнение 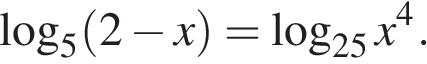
б) Укажите корни этого уравнения, принадлежащие отрезку 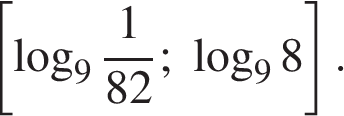
Решение.
а) Запишем исходное уравнение в виде:
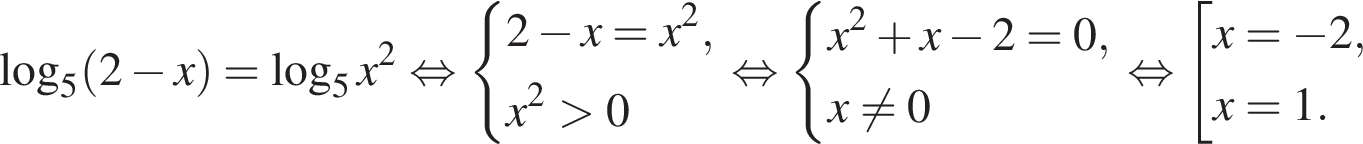
б) Поскольку 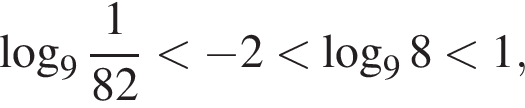 отрезку
отрезку 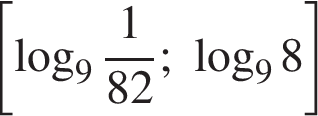 принадлежит единственный корень −2.
принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
14.Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α содержащей прямую BD1 и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями α и BCC1, если AA1 = 6, AB = 4.
Решение.
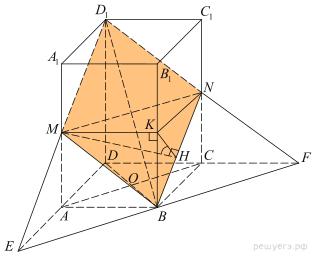
Плоскость  проходит через точку В, лежащую в плоскости основания, и параллельна прямой AC, лежащей в плоскости основания. Следовательно, плоскость
проходит через точку В, лежащую в плоскости основания, и параллельна прямой AC, лежащей в плоскости основания. Следовательно, плоскость  пересекает плоскость основания по прямой, содержащей точку В и параллельной АС. Пусть эта прямая пересекает продолжения сторон DA и DC основания в точках E и F соответственно. Тогда
пересекает плоскость основания по прямой, содержащей точку В и параллельной АС. Пусть эта прямая пересекает продолжения сторон DA и DC основания в точках E и F соответственно. Тогда  пересекает плоскость боковых граней по прямым D1E и D1F. Пусть M и N — точки пересечения этих прямых с боковыми ребрами параллелепипеда, тогда BMD1N — сечение параллелепипеда плоскостью
пересекает плоскость боковых граней по прямым D1E и D1F. Пусть M и N — точки пересечения этих прямых с боковыми ребрами параллелепипеда, тогда BMD1N — сечение параллелепипеда плоскостью 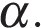
Поскольку плоскость сечения проходит через прямую EF, параллельную плоскости ACC1A1 и пересекает её по прямой MN, прямая MN параллельна EF, а значит, параллельна AC.
По условию, сечение является ромбом, диагонали ромба перпендикулярны, поэтому  и
и 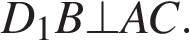 По теореме о трёх перпендикулярах, из перпендикулярности наклонной D1B и прямой AC следует перпендикулярность прямой AC проекции наклонной — прямой DB. Этим показано, что диагонали лежащего в основании прямоугольника взаимно перпендикулярны. Следовательно, этот прямоугольник является квадратом, что и требовалось доказать.
По теореме о трёх перпендикулярах, из перпендикулярности наклонной D1B и прямой AC следует перпендикулярность прямой AC проекции наклонной — прямой DB. Этим показано, что диагонали лежащего в основании прямоугольника взаимно перпендикулярны. Следовательно, этот прямоугольник является квадратом, что и требовалось доказать.
Приведем другое рассуждение. Диагонали ромба точкой пересечения делятся пополам, поэтому MN проходит через середину D1B. Кроме того, прямая MN параллельна прямой AC, а значит, и прямой EF. Из этого следует, что MN — средняя линия треугольника ED1F, а тогда точки M и N — середины рёбер параллелепипеда. Прямоугольные треугольники ABM и 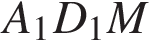 равны по гипотенузе и катету:
равны по гипотенузе и катету: 
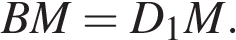 Значит,
Значит, 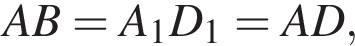 а ABCD является квадратом.
а ABCD является квадратом.
б) Пусть K — середина ребра BB1 а KH — высота треугольника BKN. Тогда плоскость MKH перпендикулярна прямой BN. Значит, угол MHK — линейный угол искомого двугранного угла. (Или: проведём перпендикуляры MK и KH, по теореме о трёх перпендикулярах MH — также перпендикуляр к BN, поэтому MHK — линейный угол искомого двугранного угла).
В прямоугольном треугольнике BKN имеем: 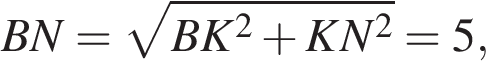
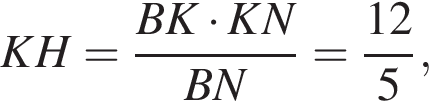
откуда
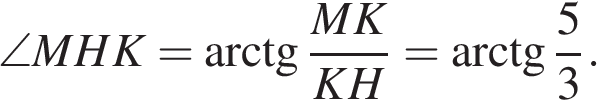
Иначе. Сечение является ромбом, площадь ромба равна половине произведения его диагоналей: 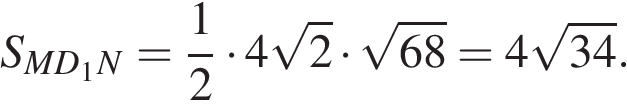 Проекцией ромба сечения на боковую грань ВСС1В1 является параллелограмм ВKС1N, площадь которого равна половине площади прямоугольника ВСС1В1 то есть 12. Поскольку
Проекцией ромба сечения на боковую грань ВСС1В1 является параллелограмм ВKС1N, площадь которого равна половине площади прямоугольника ВСС1В1 то есть 12. Поскольку  для искомого угла между плоскостями получаем:
для искомого угла между плоскостями получаем:
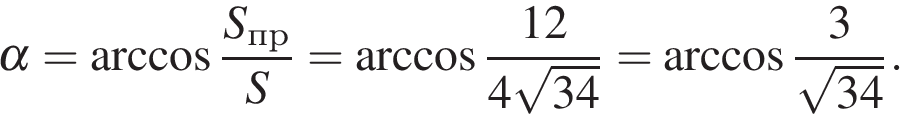
Ответ: 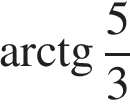 или
или 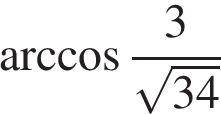 .
.
15.Решите неравенство: 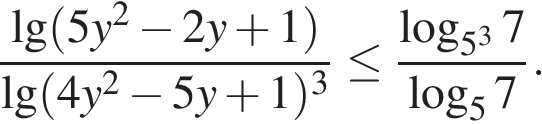
Решение.
Используя свойства логарифмов, преобразуем неравенство:
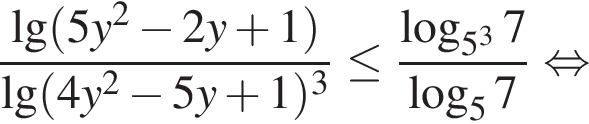
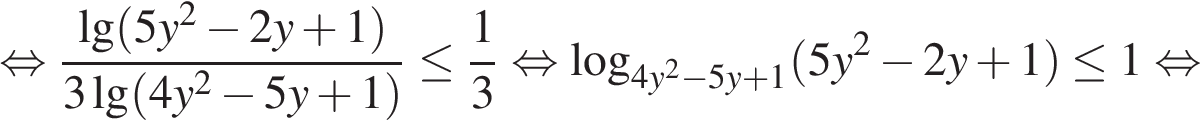
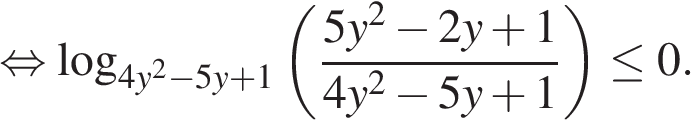
Перейдём к системе:
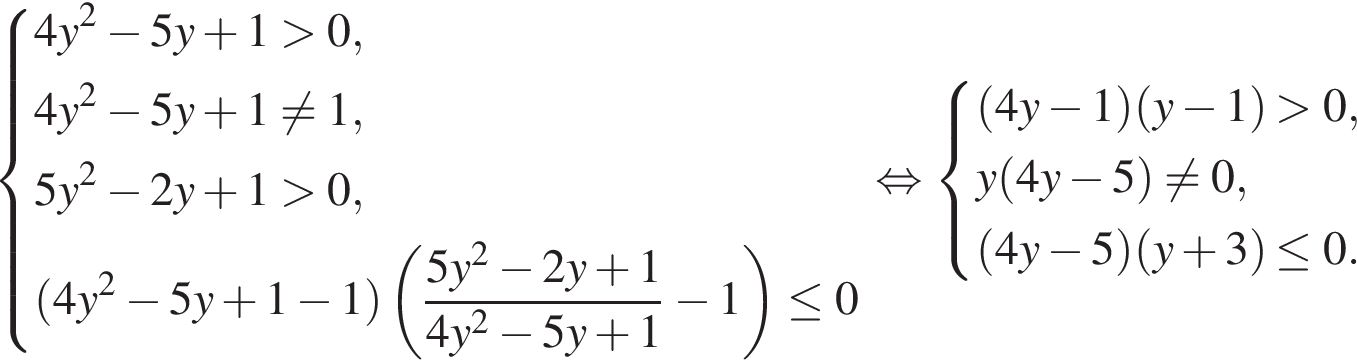
Решение первого неравенства: 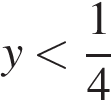 или
или  Из второго равенства получаем, что
Из второго равенства получаем, что  и
и 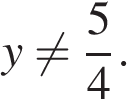 Решение третьего неравенства:
Решение третьего неравенства: 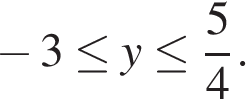
Таким образом, решением неравенства является множество 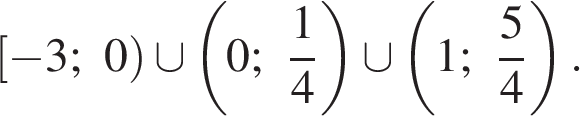
Ответ: 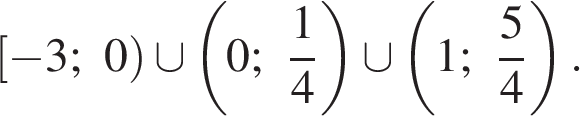
16.Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.
Решение.
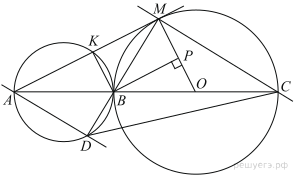 а) Точки M и D лежат на окружностях с диаметрами BC и AB соответственно, поэтому
а) Точки M и D лежат на окружностях с диаметрами BC и AB соответственно, поэтому
Прямые AD и MC перпендикулярны одной и той же прямой MD, следовательно, прямые AD и MC параллельны.
б) Пусть O — центр окружности с диаметром BC. Тогда прямые OM и AM перпендикулярны. Учитывая, что прямые BK и AM перпендикулярны, получаем, что прямые OM и BK параллельны. Обозначим BK через x. Треугольник AMO подобен треугольнику AKB с коэффициентом 5, поэтому OB = OM = 5x. Опустим перпендикуляр BP из точки B на прямую OM. Так как четырёхугольник BKMP — прямоугольник,


По теореме Пифагора OB2 = BP2 + OP2, откуда 25x2 = 144 + 16x2. Получаем, что x = 4.
Поскольку прямые AD и MC параллельны,

Значит, треугольники DBC и AMB равновелики. Следовательно,
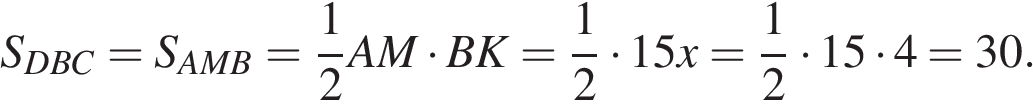
Ответ: 30.
17.В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.
Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?
Решение.
Если искомая сумма составляет S рублей, то при коэффициенте ежегодной процентной ставки q, равной 1,31, фиксированная сумма  которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет
которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет  откуда
откуда 
Заметим, что 69 690 821 кратно  Действительно,
Действительно, 
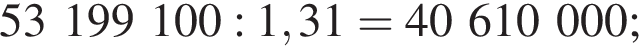
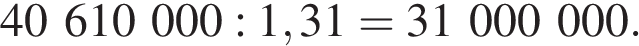
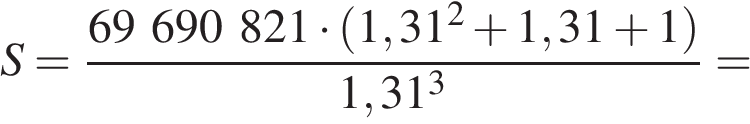
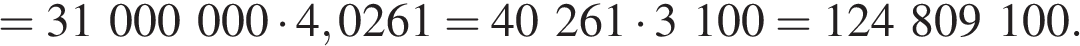
Ответ: 124 809 100 рублей.
Замечания:
1. В мировой практике существует и работает два способа (схемы) погашения кредитов:
дифференцированная, при которой периодический платеж включает постоянную сумма для погашения основного долга по кредиту, к которой прибавляются проценты на оставшуюся часть долга;
аннуитетная (равными платежами), как в условии данной задачи.
2. При аннуитетной схеме, как правило, бывает кратным  либо фиксированная сумма, которую клиент обязан вносить в отчетный период, либо сумма взятого кредита. Возможен случай, когда та или другая сумма, указанная выше, кратна
либо фиксированная сумма, которую клиент обязан вносить в отчетный период, либо сумма взятого кредита. Возможен случай, когда та или другая сумма, указанная выше, кратна 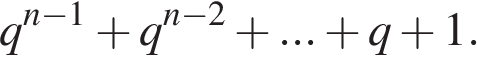
3. Прежде чем приступить к решению задачи, лучше проверить ожидаемые кратности, что облегчит дальнейшие вычисления.
Приведём другое решение:
Если искомая сумма составляет x рублей, то:
Периоды
Долг клиента (рублей)
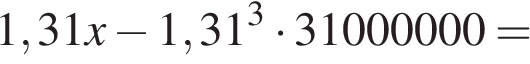
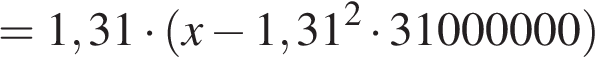


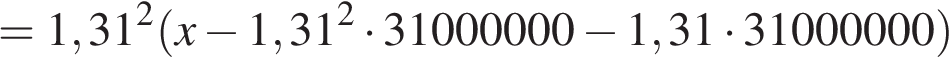
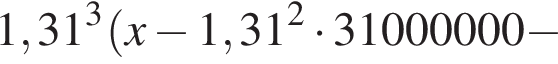
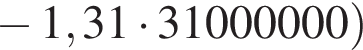

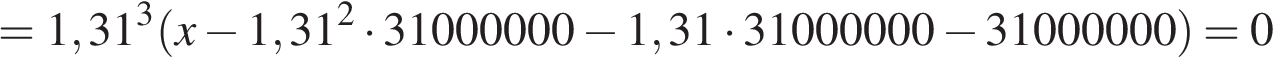
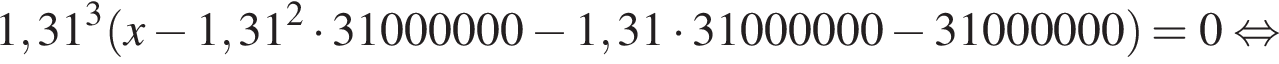
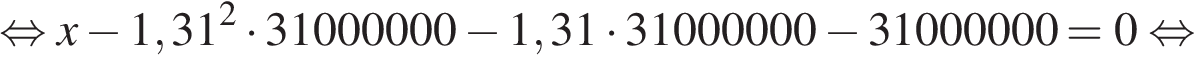

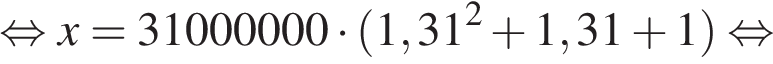
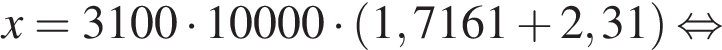
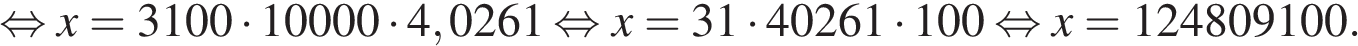
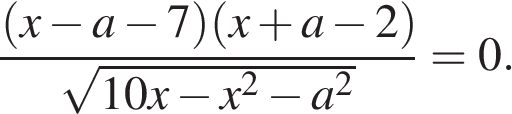
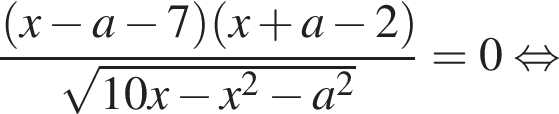
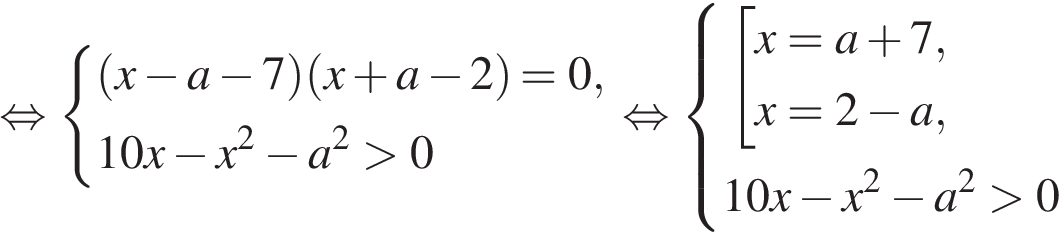
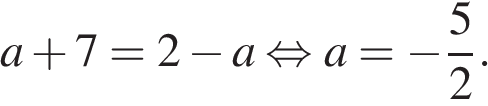 Тогда корень
Тогда корень 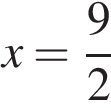 принадлежит отрезку [4; 8] и удовлетворяет ОДЗ.
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ.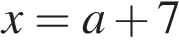 принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если второй корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем: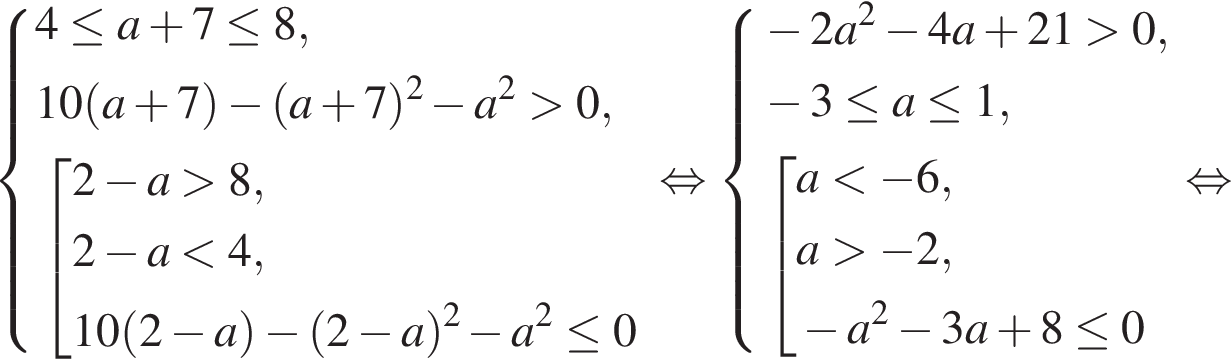
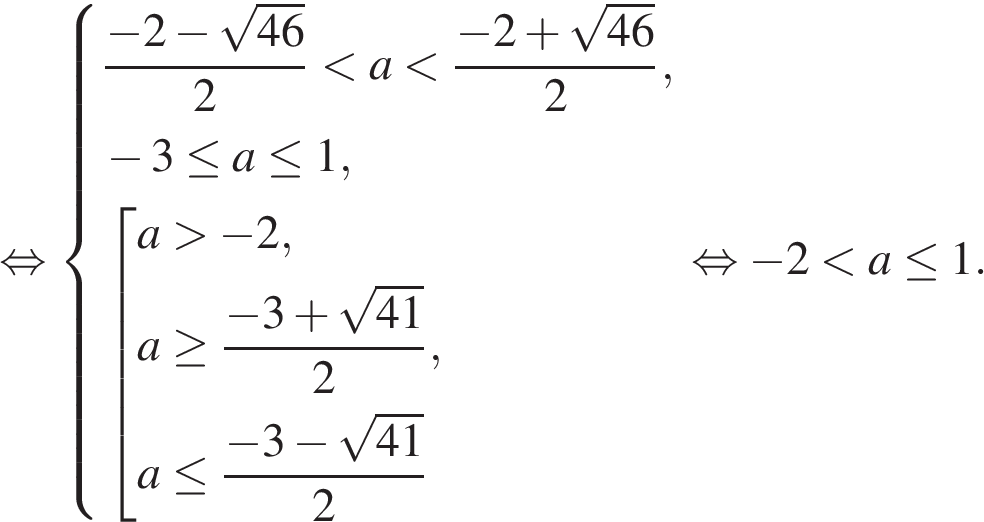
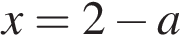 принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем:
принадлежит отрезку [4; 8] и удовлетворяет ОДЗ. Тогда уравнение имеет единственное решение на заданном отрезке, если первый корень не принадлежит отрезку [4; 8] или не удовлетворяет ОДЗ. Имеем: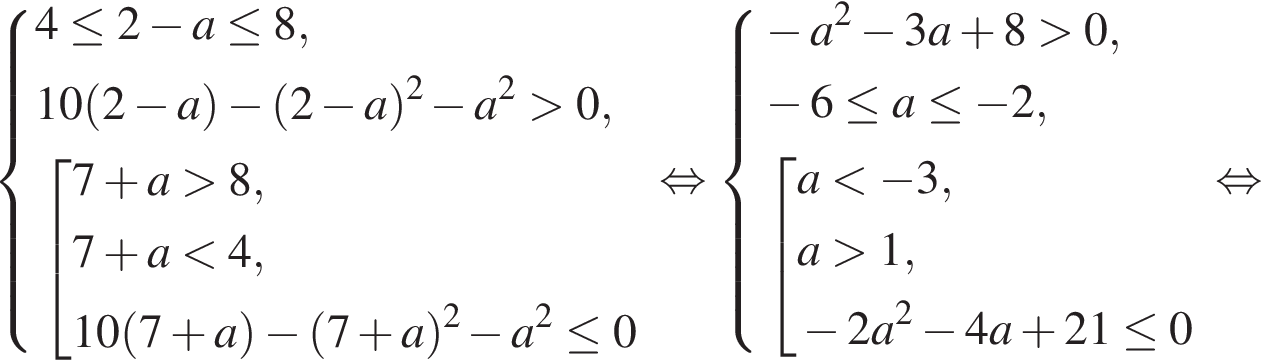
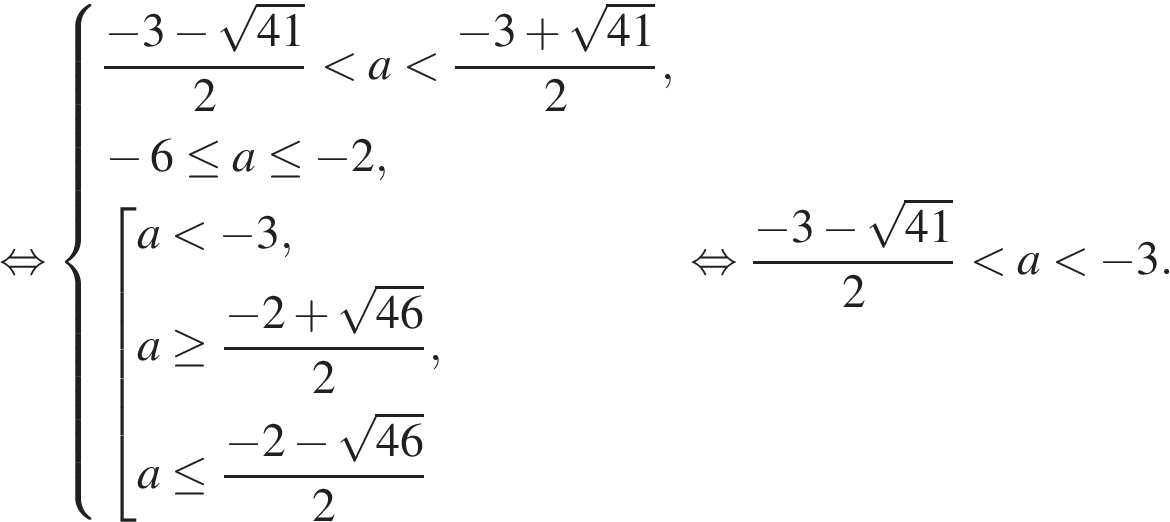
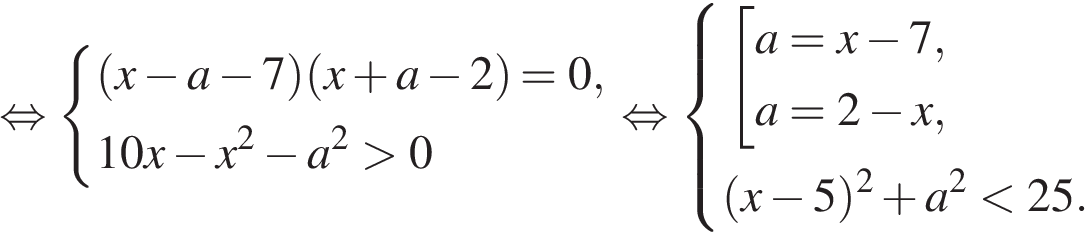
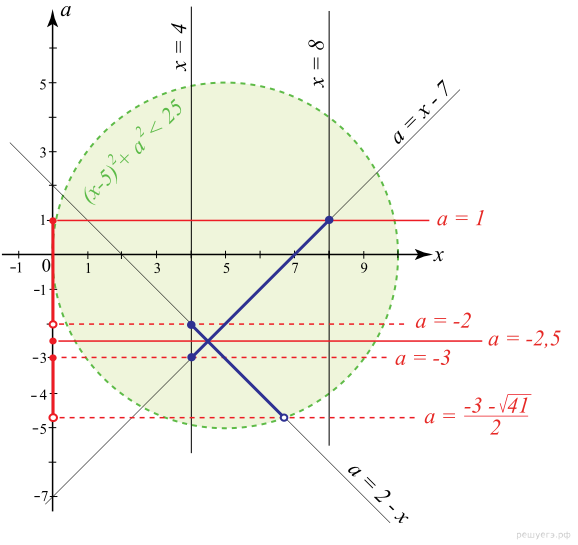
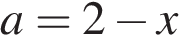 и
и 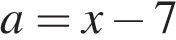 , лежащие внутри круга, ограниченного окружностью
, лежащие внутри круга, ограниченного окружностью  .
.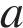 (значения ординаты), при которых уравнение имеет единственное решение на отрезке [4; 8].
(значения ординаты), при которых уравнение имеет единственное решение на отрезке [4; 8].
 найдём, подставив в уравнение окружности
найдём, подставив в уравнение окружности 
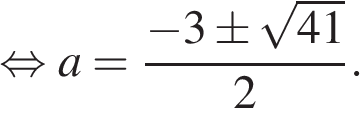
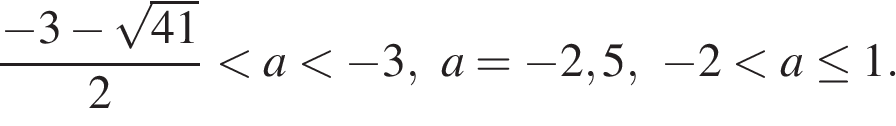
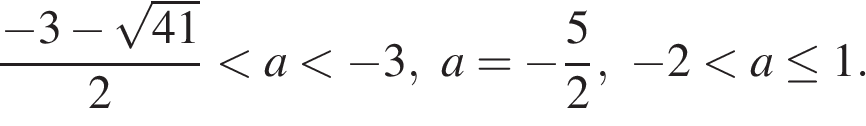
 , а сумма всех чисел, кроме будущих нулей, равна
, а сумма всех чисел, кроме будущих нулей, равна 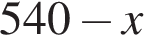 , и их
, и их 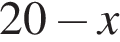 штук.
штук.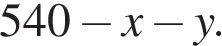 Значит,
Значит,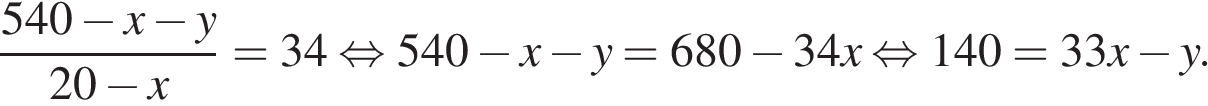
 Но тогда
Но тогда  , что невозможно.
, что невозможно.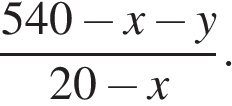 Очевидно, следует взять
Очевидно, следует взять  и максимизировать
и максимизировать 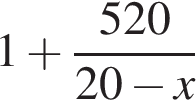 , то есть следует максимизировать x.
, то есть следует максимизировать x. , откуда
, откуда  ,
,  ,
,  Тогда требуемое выражение будет равно
Тогда требуемое выражение будет равно 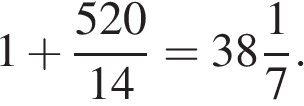 Это возможно, например, для набора из шести единиц, числа 14 и тринадцати чисел по 40, из которых уменьшают все единицы и только их, получая
Это возможно, например, для набора из шести единиц, числа 14 и тринадцати чисел по 40, из которых уменьшают все единицы и только их, получая